
Illustrative Math Alignment: Grade 6 Unit 9
Putting it All Together
Lesson 1: Fermi Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|

|
SAT Math Lesson Plan 12: Measures of Central Tendency |
|
Data Analysis |

|
SAT Math Lesson Plan 11: Data Interpretation |
|
Data Analysis |

|
Lesson Plan--Linear Functions and Equations (HS)--Lesson 6--Linear Regression | Lesson Plan: Linear Regression and Finding the Line of Best Fit In this comprehensive lesson, high school students delve into the fundamentals of linear regression, a pivotal statistical method for modeling relationships between two quantitative variables. Through interactive activities, students will: |
Data Analysis and Applications of Linear Functions |

|
Video Definition 26--Linear Function Concepts--Correlation Coefficient | Video Definition 26--Linear Function Concepts--Correlation Coefficient
TopicLinear Functions DescriptionThe term is "Correlation Coefficient," defined as a numerical measure quantifying the strength and direction of the linear relationship between two variables, ranging from -1 to 1. A scatterplot and calculation examples are provided to illustrate this concept. This term connects linear functions to data analysis, showing how linear relationships are quantified in statistics. |
Data Analysis |
|
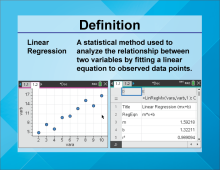
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |
|
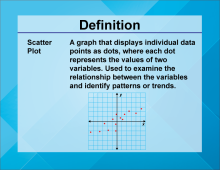
Video Definition 23--Linear Function Concepts--Scatter Plot | Video Definition 23--Linear Function Concepts--Scatter Plot
TopicLinear Functions DescriptionThe term is "Scatter Plot," defined as a graph displaying individual data points as dots, where each dot represents the values of two variables. Used to examine relationships and identify patterns or trends. This term provides a graphical tool to visualize and analyze linear relationships in data. |
Data Analysis |
|
Instructional Resource--Segmented Bar Graphs | Instructional Resource | Constructing a Segmented Bar Graph
This tutorial goes over the construction of a segmented bar graph, along with how it differs from other chart types. —PRESS PREVIEW TO VIEW THE ACTIVITY— To see the complete collection of Instructional Resources, click on this link.Note: The download is a PDF file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 120--Will Avatar Repeat? | Math in the News: Issue 120 | Will Avatar Repeat?
December 2022. In this issue of Math in the News we look at box office data for he new Avatar sequel. Will it have the same success? —PRESS PREVIEW TO SEE THE SLIDE SHOW— This is part of the Math in the News collection. To see the complete collection, click on this link.Note: The download is a PPT file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Gathering and Data Analysis |

|
Math in the News: Issue 117--Box Office Hits and Misses | Math in the News: Issue 117 | Box Office Hits and Misses
December 2022. In this issue of Math in the News we look at box office hits and misses from Disney. The House of Blockbosters every now and then misfires. It's useful to analyze box office data to see what we can learn from the hits and misses. —PRESS PREVIEW TO SEE THE SLIDE SHOW— This is part of the Math in the News collection. To see the complete collection, click on this link.Note: The download is a PPT file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Definition--Charts and Graphs--Categorical Data | Definition--Charts and Graphs--Categorical Data
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Continuous Data | Definition--Charts and Graphs--Continuous Data
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
Definition--Charts and Graphs--Discrete Data | Definition--Charts and Graphs--Discrete Data
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
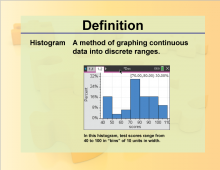
Definition--Charts and Graphs--Histogram | Definition--Charts and Graphs--Histogram
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Two-Way Frequency Table | Definition--Charts and Graphs--Two-Way Frequency Table
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
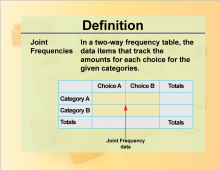
Definition--Charts and Graphs--Joint Frequencies | Definition--Charts and Graphs--Joint Frequencies
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
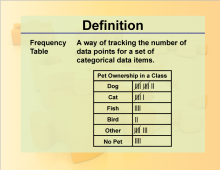
Definition--Charts and Graphs--Frequency Table | Definition--Charts and Graphs--Frequency Table
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Scaled Pictograph | Definition--Charts and Graphs--Scaled Pictograph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Pictograph | Definition--Charts and Graphs--Pictograph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Stem-and-Leaf Plot | Definition--Charts and Graphs--Stem-and-Leaf Plot
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
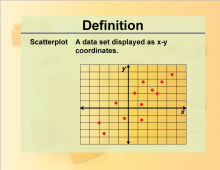
Definition--Charts and Graphs--Scatterplot | Definition--Charts and Graphs--Scatterplot
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Math Example--Combinatorics--Factorial Expressions: Example 1 | Math Example--Combinatorics--Factorial Expressions: Example 1
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Data Analysis and Combinatorics |

|
Instructional Resource: Quadratic Regression on Desmos | INSTRUCTIONAL RESOURCE: Tutorial: Quadratic Regression on Desmos
In this tutorial we walk students through the steps of doing a quadratic regression on a Desmos graphing calculator. The steps include showing how to create pseudo-quadratic data on a spreadsheet. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions and Data Analysis |
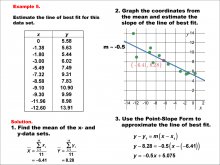
|
Math Example--Charts, Graphs, and Plots--Estimating the Line of Best Fit: Example 5 | Math Example--Charts, Graphs, and Plots-- Estimating the Line of Best Fit: Example 5
In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models. |
Point-Slope Form, Slope-Intercept Form and Data Analysis |
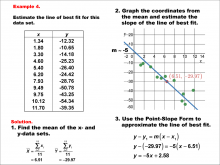
|
Math Example--Charts, Graphs, and Plots--Estimating the Line of Best Fit: Example 4 | Math Example--Charts, Graphs, and Plots-- Estimating the Line of Best Fit: Example 4
In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models. |
Point-Slope Form, Slope-Intercept Form and Data Analysis |
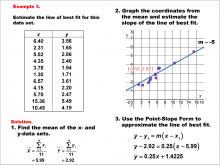
|
Math Example--Charts, Graphs, and Plots--Estimating the Line of Best Fit: Example 3 | Math Example--Charts, Graphs, and Plots-- Estimating the Line of Best Fit: Example 3
In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models. |
Point-Slope Form, Slope-Intercept Form and Data Analysis |
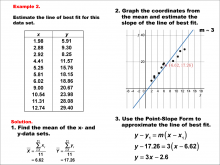
|
Math Example--Charts, Graphs, and Plots--Estimating the Line of Best Fit: Example 2 | Math Example--Charts, Graphs, and Plots-- Estimating the Line of Best Fit: Example 2
In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models. |
Point-Slope Form, Slope-Intercept Form and Data Analysis |
|
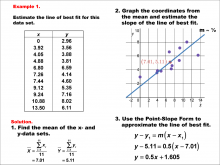
Math Example--Charts, Graphs, and Plots--Estimating the Line of Best Fit: Example 1 | Math Example--Charts, Graphs, and Plots-- Estimating the Line of Best Fit: Example 1
In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models. |
Slope-Intercept Form and Data Analysis |

|
Video Tutorial: Line of Best Fit | Video Tutorial: Line of Best Fit
This video looks at the Line of Best Fit. A real-world data set is analyzed, from which a linear function in slope-intercept is derived. Students are shown how to find the line of best fit using a TI graphing calculator. Strategies for estimating the line of best fit are also explored. |
Slope-Intercept Form and Data Analysis |

|
Math in the News: Issue 116: The 2021 Olympics | Math in the News: Issue 116: The 2021 Olympics
August 2021. In this issue of Math in the News we look at various charts and statistics about the Tokyo Olympics. Students are shown a series of charts and are then asked questions to encourage them to analyze the data. This is an excellent back-to-school activity with the focus on real-world data. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Why Are Receipts So Long? | INSTRUCTIONAL RESOURCE: Algebra Application: Why Are Receipts So Long?
In this Algebra Application, students gather data to study the lengths of paper receipts. They also learn to estimate the total number of receipts produced worldwide using industry data. From this they can study the environmental impact of having to produce so many paper receipts. The math topics covered include: Measures of central tendency (specifically the mean), Scientific notation, Rates, Converting different units. The culminating activity is for students to make a persuasive case to retailers about finding alternatives to paper receipts, using the data they gathered and analyzed. This is a great back-to-school activity for middle school or high school students. A relevant real-world application allows them to review math concepts. |
Laws of Exponents and Data Analysis |

|
Definition--Measures of Central Tendency--Standard Deviation | Standard DeviationTopicStatistics DefinitionStandard deviation is a measure of the amount of variation or dispersion in a set of values. DescriptionStandard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Average | AverageTopicStatistics DefinitionThe average is a measure of central tendency, calculated by dividing the sum of values by their count. DescriptionIn statistics, the average is crucial for analyzing data sets, revealing trends, and providing insight into overall performance. It’s applicable in various fields, from school grades to business metrics. For example, if a student scores 80, 90, and 100 on three exams, the average can be calculated as follows: Average = (80 + 90 + 100) / 3 = 90. The average is essential in math education as it forms a foundational concept for more advanced statistical analyses. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Average | Weighted AverageTopicStatistics DefinitionA weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. DescriptionThe weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Average Speed | Average SpeedTopicStatistics DefinitionAverage speed is the total distance traveled divided by the total time taken. DescriptionThis concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations. |
Data Analysis |

|
Definition--Measures of Central Tendency--Sample Mean | Sample MeanTopicStatistics DefinitionThe sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. DescriptionThe sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations. |
Data Analysis |

|
Definition--Measures of Central Tendency--Population Mean | Population MeanTopicStatistics DefinitionThe population mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon. |
Data Analysis |

|
Definition--Measures of Central Tendency--Geometric Mean | Geometric MeanTopicStatistics DefinitionThe geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. DescriptionThe geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay. |
Data Analysis |

|
Definition--Measures of Central Tendency--Quartile | QuartileTopicStatistics DefinitionQuartiles divide a ranked data set into four equal parts. DescriptionQuartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends. |
Data Analysis |
|
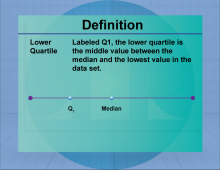
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Upper Quartile | Upper QuartileTopicStatistics DefinitionThe upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. DescriptionThe upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels. |
Data Analysis |
|
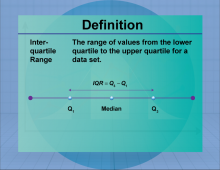
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |

|
Definition--Measures of Central Tendency--Continuous Data | Continuous DataTopicStatistics DefinitionContinuous data is numerical data that can take any value within a range. DescriptionContinuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus. |
Data Analysis |

|
Definition--Measures of Central Tendency--Histogram | HistogramTopicStatistics DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference. |
Data Analysis |
|
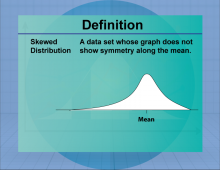
Definition--Measures of Central Tendency--Skewed Distribution | Skewed DistributionTopicStatistics DefinitionA skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. DescriptionSkewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution. |
Data Analysis |

|
Definition--Measures of Central Tendency--Symmetric Distribution | Symmetric DistributionTopicStatistics DefinitionA symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. DescriptionSymmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed. |
Data Analysis |

|
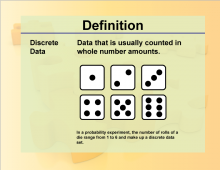
Definition--Measures of Central Tendency--Discrete Data | Discrete DataTopicStatistics DefinitionDiscrete data consists of countable values, often represented by whole numbers. DescriptionDiscrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations. |
Data Analysis |