
Illustrative Math Alignment: Grade 7 Unit 4
Proportional Relationships and Percentages
Lesson 1: Lots of Flags
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Example--Percents--Equations with Percents: Example 2 | Math Example--Percents--Equations with Percents: Example 2TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 7% of 9.5?" The solution involves converting 7% to its decimal equivalent, 0.07, and then multiplying it by 9.5 to obtain the result of 0.665. This example builds upon the previous one by introducing a decimal number as the base value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 20 | Math Example--Percents--Equations with Percents: Example 20TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "32 is what percent of 1.5?" The solution involves setting up the equation 1.5 * (x / 100) = 32, then solving for x to get x = 32 * (100 / 1.5), which equals 2133.3%. This example introduces a scenario where the resulting percentage is significantly larger than 100% and involves a decimal base number less than 1. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 21 | Math Example--Percents--Equations with Percents: Example 21TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "48 is what percent of 55?" The solution involves setting up the equation 55 * (x / 100) = 48, then solving for x to get x = 48 * (100 / 55), which equals 87.27%. This example demonstrates how to calculate a percentage when the two numbers are relatively close in value, resulting in a percentage close to but less than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 22 | Math Example--Percents--Equations with Percents: Example 22TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "52.2 is what percent of 98.5?" The solution involves setting up the equation 98.5 * (x / 100) = 52.2, then solving for x to get x = 52.2 * (100 / 98.5), which is approximately 52.99%. This example introduces a scenario where both the numerator and denominator are decimal numbers, resulting in a percentage that is also close to the original numerator. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 23 | Math Example--Percents--Equations with Percents: Example 23TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "68 is what percent of 320?" The solution involves setting up the equation 320 * (x / 100) = 68, then solving for x to get x = 68 * (100 / 320), which equals 21.25%. This example demonstrates how to calculate a percentage when dealing with whole numbers, resulting in a percentage that's less than 25%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 24 | Math Example--Percents--Equations with Percents: Example 24TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "75.5 is what percent of 555.25?" The solution involves setting up the equation 555.25 * (x / 100) = 75.5, then solving for x to get x = 75.5 * (100 / 555.25), which is approximately 13.59%. This example introduces a scenario where both the numerator and denominator are decimal numbers, resulting in a percentage that's less than 15%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 25 | Math Example--Percents--Equations with Percents: Example 25TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "125 is what percent of 2?" The solution involves setting up the equation 2 * (x / 100) = 125, then solving for x to get x = 125 * (100 / 2), which equals 6250%. This example demonstrates how to calculate a percentage when the first number is significantly larger than the second, resulting in a percentage well over 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 26 | Math Example--Percents--Equations with Percents: Example 26TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "300 is what percent of 3.5?" The solution involves setting up the equation 3.5 * (x / 100) = 300, then solving for x to get x = 300 * (100 / 3.5), which equals 8571.43%. This example introduces a scenario where the resulting percentage is extremely large, over 8000%, due to the first number being significantly larger than the small decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 27 | Math Example--Percents--Equations with Percents: Example 27TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "278 is what percent of 99?" The solution involves setting up the equation 99 * (x / 100) = 278, then solving for x to get x = 278 * (100 / 99), which equals 280.80%. This example demonstrates how to calculate a percentage when the first number is significantly larger than the second, resulting in a percentage greater than 200%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 28 | Math Example--Percents--Equations with Percents: Example 28TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "300 is what percent of 75.5?" The solution involves setting up the equation 75.5 * (x / 100) = 300, then solving for x to get x = 300 * (100 / 75.5), which equals 397.35%. This example introduces a scenario where the resulting percentage is close to 400%, with the first number being significantly larger than the decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 29 | Math Example--Percents--Equations with Percents: Example 29TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is what percent of 220?" The solution involves setting up the equation 220 * (x / 100) = 400, then solving for x to get x = 400 * (100 / 220), which equals 181.81%. This example demonstrates how to calculate a percentage when the first number is nearly double the second, resulting in a percentage between 150% and 200%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 3 | Math Example--Percents--Equations with Percents: Example 3TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 8% of 58?" The solution involves converting 8% to its decimal form, 0.08, and then multiplying it by 58 to arrive at the answer of 4.64. This example introduces a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 30 | Math Example--Percents--Equations with Percents: Example 30TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "333.5 is what percent of 500.25?" The solution involves setting up the equation 500.25 * (x / 100) = 333.5, then solving for x to get x = 333.5 * (100 / 500.25), which is approximately 66.67%. This example introduces a scenario where both numbers are decimals and the resulting percentage is less than 100%, showing how to handle more complex decimal calculations. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 31 | Math Example--Percents--Equations with Percents: Example 31TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "4 is 0.1% of what number?" The solution involves setting up the equation 4 = 0.001 * x, then solving for x to get x = 4 / 0.001, which equals 4000. This example demonstrates how to calculate the whole when given a very small percentage of it, resulting in a much larger number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 32 | Math Example--Percents--Equations with Percents: Example 32TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "7 is 1% of what number?" The solution involves setting up the equation 7 = 0.01 * x, then solving for x to get x = 7 / 0.01, which equals 700. This example introduces a scenario where we need to find the whole when given a small percentage of it, resulting in a number 100 times larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 33 | Math Example--Percents--Equations with Percents: Example 33TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "9 is 30% of what number?" The solution involves setting up the equation 9 = 0.3 * x, then solving for x to get x = 9 / 0.3, which equals 30. This example demonstrates how to calculate the whole when given a larger percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 34 | Math Example--Percents--Equations with Percents: Example 34TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "1 is 400% of what number?" The solution involves setting up the equation 1 = 4.0 * x, then solving for x to get x = 1 / 4, which equals 0.25. This example introduces a scenario where we need to find a number that, when increased by 400%, results in 1, leading to a fraction or decimal less than 1. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 35 | Math Example--Percents--Equations with Percents: Example 35TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "15 is 0.25% of what number?" The solution involves setting up the equation 15 = 0.0025 * x, then solving for x to get x = 15 / 0.0025, which equals 6000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 36 | Math Example--Percents--Equations with Percents: Example 36TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "30 is 5% of what number?" The solution involves setting up the equation 30 = 0.05 * x, then solving for x to get x = 30 / 0.05, which equals 600. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a much larger number. |
Solving Percent Equations |
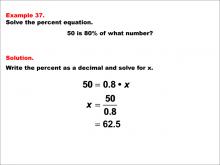
|
Math Example--Percents--Equations with Percents: Example 37 | Math Example--Percents--Equations with Percents: Example 37TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "50 is 80% of what number?" The solution involves setting up the equation 50 = 0.8 * x, then solving for x to get x = 50 / 0.8, which equals 62.5. This example introduces a scenario where we need to find the whole when given a large percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |
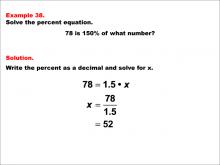
|
Math Example--Percents--Equations with Percents: Example 38 | Math Example--Percents--Equations with Percents: Example 38TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "78 is 150% of what number?" The solution involves setting up the equation 78 = 1.5 * x, then solving for x to get x = 78 / 1.5, which equals 52. This example demonstrates how to calculate the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |
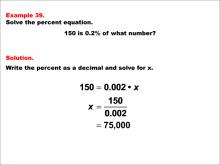
|
Math Example--Percents--Equations with Percents: Example 39 | Math Example--Percents--Equations with Percents: Example 39TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "150 is 0.2% of what number?" The solution involves setting up the equation 150 = 0.002 * x, then solving for x to get x = 150 / 0.002, which equals 75,000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 4 | Math Example--Percents--Equations with Percents: Example 4TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 6.5% of 45.5?" The solution involves converting 6.5% to its decimal equivalent, 0.065, and then multiplying it by 45.5 to obtain the result of 2.9575. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation. |
Solving Percent Equations |
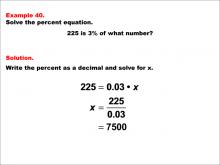
|
Math Example--Percents--Equations with Percents: Example 40 | Math Example--Percents--Equations with Percents: Example 40TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "225 is 3% of what number?" The solution involves setting up the equation 225 = 0.03 * x, then solving for x to get x = 225 / 0.03, which equals 7,500. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 41 | Math Example--Percents--Equations with Percents: Example 41TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is 40% of what number?" The solution involves setting up the equation 400 = 0.4 * x, then solving for x to get x = 400 / 0.4, which equals 1000. This example demonstrates how to calculate the whole when given a significant percentage of it, resulting in a number that is larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 42 | Math Example--Percents--Equations with Percents: Example 42TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "650 is 130% of what number?" The solution involves setting up the equation 650 = 1.3 * x, then solving for x to get x = 650 / 1.3, which equals 500. This example introduces a scenario where we need to find the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 5 | Math Example--Percents--Equations with Percents: Example 5TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 30% of 9?" The solution involves converting 30% to its decimal form, 0.3, and then multiplying it by 9 to get the result of 2.7. This example introduces a larger percentage, demonstrating how the method applies consistently across various percentage values. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 6 | Math Example--Percents--Equations with Percents: Example 6TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 28% of 7.2?" The solution involves converting 28% to its decimal equivalent, 0.28, and then multiplying it by 7.2 to obtain the result of 2.016. This example combines a whole number percentage with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 7 | Math Example--Percents--Equations with Percents: Example 7TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 45% of 68?" The solution involves converting 45% to its decimal form, 0.45, and then multiplying it by 68 to arrive at the answer of 30.6. This example introduces a larger percentage and a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 8 | Math Example--Percents--Equations with Percents: Example 8TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 52.3% of 36.9?" The solution involves converting 52.3% to its decimal equivalent, 0.523, and then multiplying it by 36.9 to obtain the result of 19.2987. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation and showcasing the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 9 | Math Example--Percents--Equations with Percents: Example 9TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 150% of 8?" The solution involves converting 150% to its decimal form, 1.5, and then multiplying it by 8 to get the result of 12. This example introduces a percentage greater than 100%, demonstrating how the method applies consistently even when dealing with percentages that represent values larger than the whole. |
Solving Percent Equations |
|
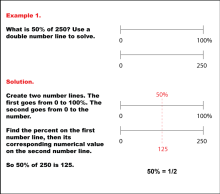
Math Example: Percents with Double Number Lines: Example 1 | Math Example: Percents with Double Number Lines: Example 1TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 50% of 250 using a double number line. The solution shows two parallel number lines: one ranging from 0 to 100% and the other from 0 to 250. By aligning 50% on the percentage line with its corresponding value on the numerical line, we can see that 50% of 250 is 125. This method visually represents the concept that 50% is equivalent to one-half of a quantity. |
Ratios and Rates |
|
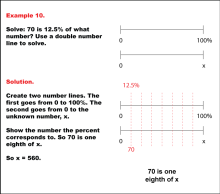
Math Example: Percents with Double Number Lines: Example 10 | Math Example: Percents with Double Number Lines: Example 10TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine an unknown value using a double number line when given a part and its corresponding percentage, involving a decimal percentage. The image shows two number lines: one ranging from 0 to 100% and another from 0 to an unknown number x. The position 70 is marked on the second line, visually illustrating the process of finding x when 70 is 12.5% of x. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 11 | Math Example: Percents with Double Number Lines: Example 11TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 75, with 25 marked as an intermediate point. This visual representation helps students understand the relationship between the part (25) and the whole (75) in percentage terms. |
Ratios and Rates |
|
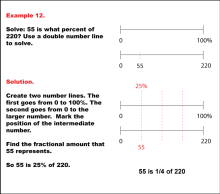
Math Example: Percents with Double Number Lines: Example 12 | Math Example: Percents with Double Number Lines: Example 12TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate what percent one number is of another using a double number line. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to 220, with 55 marked as an intermediate point. This visual representation helps students understand the relationship between the part (55) and the whole (220) in percentage terms. |
Ratios and Rates |
|
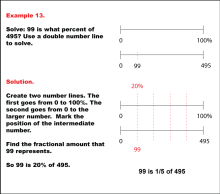
Math Example: Percents with Double Number Lines: Example 13 | Math Example: Percents with Double Number Lines: Example 13TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 495, with 99 marked as an intermediate point. This visual representation helps students understand the relationship between the part (99) and the whole (495) in percentage terms. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 14 | Math Example: Percents with Double Number Lines: Example 14TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate what percent one number is of another using a double number line. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to 396, with 198 marked at the midpoint. This visual representation helps students understand the relationship between the part (198) and the whole (396) in percentage terms. |
Ratios and Rates |
|
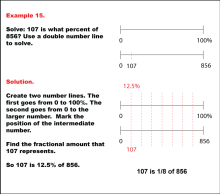
Math Example: Percents with Double Number Lines: Example 15 | Math Example: Percents with Double Number Lines: Example 15TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line, particularly when dealing with more complex ratios. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 856, with 107 marked at an eighth of the way. This visual representation helps students understand the relationship between the part (107) and the whole (856) in percentage terms. |
Ratios and Rates |
|
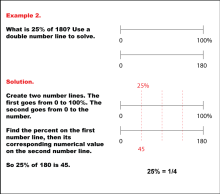
Math Example: Percents with Double Number Lines: Example 2 | Math Example: Percents with Double Number Lines: Example 2TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate 25% of 180 using a double number line. The solution presents two parallel number lines: one spanning from 0 to 100% and the other from 0 to 180. By aligning 25% on the percentage line with its corresponding value on the numerical line, we can determine that 25% of 180 is 45. This method visually demonstrates that 25% is equivalent to one-quarter of a quantity. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 3 | Math Example: Percents with Double Number Lines: Example 3TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 33 1/3% of 240 using a double number line. The solution displays two parallel number lines: one ranging from 0 to 100% and the other from 0 to 240. By aligning 33 1/3% on the percentage line with its corresponding value on the numerical line, we can see that 33 1/3% of 240 is 80. This method visually represents the concept that 33 1/3% is equivalent to one-third of a quantity. |
Ratios and Rates |
|
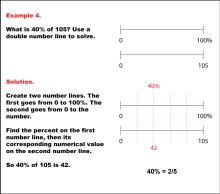
Math Example: Percents with Double Number Lines: Example 4 | Math Example: Percents with Double Number Lines: Example 4TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate 40% of 105 using a double number line. The solution presents two parallel number lines: one spanning from 0 to 100% and the other from 0 to 105. By aligning 40% on the percentage line with its corresponding value on the numerical line, we can determine that 40% of 105 is 42. This method visually demonstrates that 40% is equivalent to two-fifths of a quantity. |
Ratios and Rates |
|
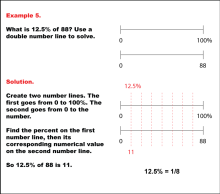
Math Example: Percents with Double Number Lines: Example 5 | Math Example: Percents with Double Number Lines: Example 5TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 12.5% of 88 using a double number line. The solution shows two parallel number lines: one ranging from 0 to 100% and the other from 0 to 88. By aligning 12.5% on the percentage line with its corresponding value on the numerical line, we can see that 12.5% of 88 is 11. This method visually represents the concept that 12.5% is equivalent to one-eighth of a quantity. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 6 | Math Example: Percents with Double Number Lines: Example 6TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to solve for an unknown value using a double number line when given a percentage. The image features two parallel number lines: one ranging from 0 to 100% and another from 0 to an unknown value x. It visually illustrates the process of determining x when 75 is 50% of x. |
Ratios and Rates |
|
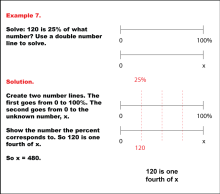
Math Example: Percents with Double Number Lines: Example 7 | Math Example: Percents with Double Number Lines: Example 7TopicRatios, Proportions, Percents DescriptionThis example illustrates how to determine an unknown value using a double number line when given a part and its corresponding percentage. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to an unknown value x. It visually demonstrates the process of finding x when 120 is 25% of x. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 8 | Math Example: Percents with Double Number Lines: Example 8TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find an unknown value using a double number line when given a part and its corresponding percentage, involving a fractional percentage. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to an unknown value x. It visually illustrates the process of determining x when 125 is 33 1/3% of x. |
Ratios and Rates |
|
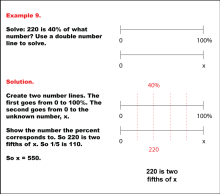
Math Example: Percents with Double Number Lines: Example 9 | Math Example: Percents with Double Number Lines: Example 9TopicRatios, Proportions, Percents DescriptionThis example illustrates how to solve for an unknown value using a double number line when given a part and its corresponding percentage. The image shows two horizontal number lines: the top line ranges from 0 to 100%, and the bottom line ranges from 0 to an unknown number x. The 40% mark on the top line aligns with 220 on the bottom line, visually demonstrating the process of finding x when 220 is 40% of x. |
Ratios and Rates |

|
Math in the News: Issue 96--The California Drought | Math in the News: Issue 96--The California Drought
July 2015. This edition of Math in the News focuses on the severe drought currently taking place in California, and how it has impacted the water resources available to the state. In this edition, students will see how to use percentages given to determine actual amounts, and to determine percents out of a whole. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents and Proportions |

|
Worksheet: Converting Percents to Decimals and Whole Numbers, Set 01 | Worksheet: Converting Percents to Decimals and Whole Numbers, Set 01 This is part of a collection of math worksheets on the topic of converting percents. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Worksheet Library To see the complete collection of Worksheets, click on this link. |
Percents |

|
Worksheet: Converting Percents to Decimals and Whole Numbers, Set 02 | Worksheet: Converting Percents to Decimals and Whole Numbers, Set 02 This is part of a collection of math worksheets on the topic of converting percents. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Worksheet Library To see the complete collection of Worksheets, click on this link. |
Percents |

|
Worksheet: Converting Percents to Decimals and Whole Numbers, Set 03 | Worksheet: Converting Percents to Decimals and Whole Numbers, Set 03 This is part of a collection of math worksheets on the topic of converting percents. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Worksheet Library To see the complete collection of Worksheets, click on this link. |
Percents |