Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 9: Dealing with Negative Numbers
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
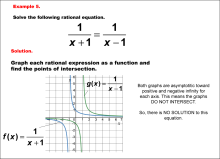
Math Example--Graphical Solutions to Rational Equations--Example 5 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
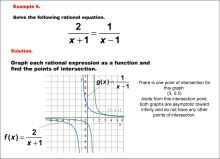
Math Example--Graphical Solutions to Rational Equations--Example 6 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
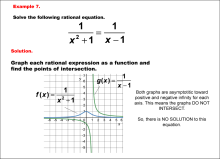
Math Example--Graphical Solutions to Rational Equations--Example 7 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
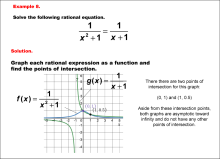
Math Example--Graphical Solutions to Rational Equations--Example 8 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
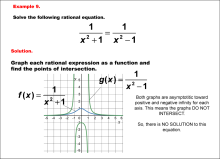
Math Example--Graphical Solutions to Rational Equations--Example 9 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 10 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 10TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation x + y = 1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = -x + 1. This simple transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 11 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 11TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation x + y = -1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = -x - 1. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 12 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 12TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation x - y = 1 from standard form to slope-intercept form. The solution process involves isolating y and changing the sign of both sides, resulting in y = x - 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13TopicLinear Functions DescriptionThis example illustrates the process of converting the linear equation -x + y = 1 from standard form to slope-intercept form. The solution involves rearranging the equation to isolate y, resulting in y = x + 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x - y = -1 from standard form to slope-intercept form. The process involves manipulating the equation to solve for y, yielding y = -x + 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation -x - y = 1 from standard form to slope-intercept form. The solution process involves isolating y, resulting in y = -x - 1. This step-by-step conversion clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x + y = -1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = x - 1. This transformation clearly reveals the slope and y-intercept of the line. Linear functions are fundamental mathematical concepts that describe relationships between two variables. The examples in this collection, such as showing step-by-step transformations from standard form to slope-intercept form, help in understanding how each part of the equation affects the graph and the relationship itself. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation x - y = -1 from standard form to slope-intercept form. The solution involves isolating y, resulting in y = x + 1. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x - y = 1 from standard form to slope-intercept form. The process involves rearranging the equation to isolate y, resulting in y = -x - 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation 12x + 28y = 0 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = -3/7 x. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation 3x + 6y = -18 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = -1/2 x - 3. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -14x - 35y = 0 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = -2/5 x. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation 28x - 21y = 0 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = 4/3 x. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation -13x + 39y = 0 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = 1/3 x. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation 5x - 2y = 12 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = 2.5x - 6. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -6x + 10y = 20 from standard form to slope-intercept form. The solution process involves isolating y and dividing by its coefficient, resulting in y = 0.6x + 2. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5TopicLinear Functions DescriptionThis example illustrates the process of converting the linear equation -9x - 15y = -45 from standard form to slope-intercept form. The solution involves rearranging the equation to isolate y, resulting in y = 3/5 x + 3. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -8x - 12y = 25 from standard form to slope-intercept form. The process involves manipulating the equation to solve for y, yielding y = -2/3 x - 25/12. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7TopicLinear Functions DescriptionThis example illustrates the transformation of the linear equation -2x + 16y = -36 from standard form to slope-intercept form. The solution process involves solving for y, resulting in y = 1/8 x - 9/4. This step-by-step conversion clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8TopicLinear Functions DescriptionThis example showcases the conversion of the linear equation -7x + 21y = 63 from standard form to slope-intercept form. The process involves rearranging the equation to isolate y, resulting in y = 1/3 x + 3. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9TopicLinear Functions DescriptionThis example demonstrates the process of converting the linear equation 10x - 28y = 56 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = (5/14)x - 2. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
|
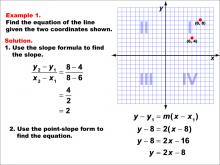
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
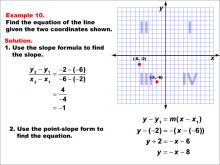
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 10 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 10
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
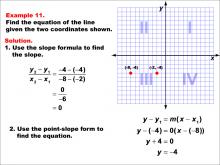
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 11 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 11
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
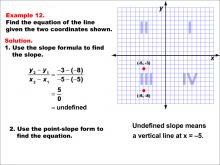
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 12 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 12
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
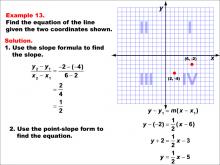
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
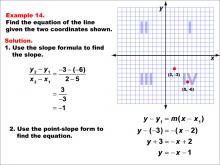
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
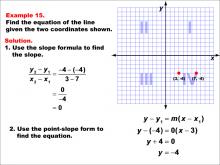
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
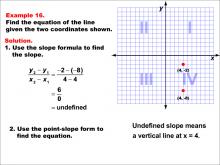
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
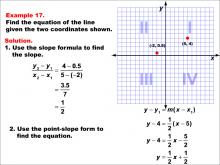
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
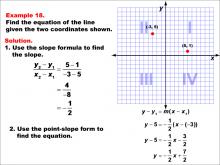
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
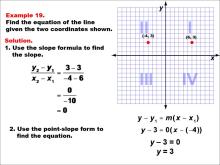
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
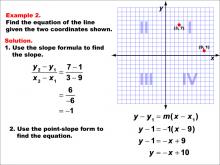
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
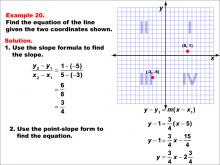
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
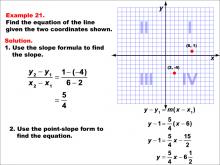
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
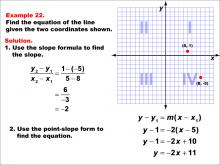
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
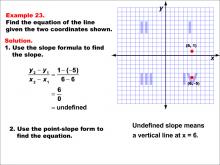
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
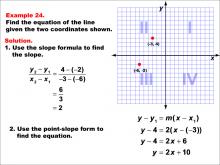
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
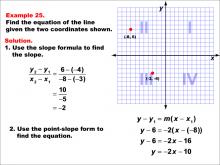
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
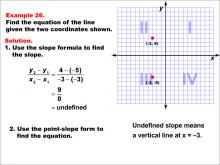
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
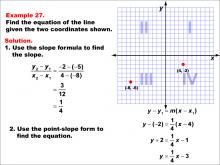
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
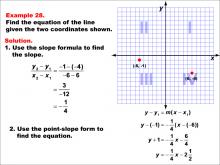
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
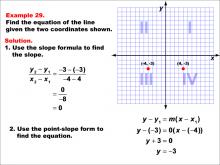
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
|
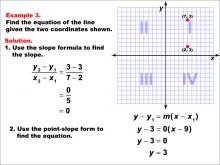
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3
This is part of a collection of math examples that focus on linear function concepts. |
Point-Slope Form and Slope-Intercept Form |
