Illustrative Math Alignment: Grade 7 Unit 9

Putting it All Together

Lesson 12: Using a Trundle Wheel to Measure Distances

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
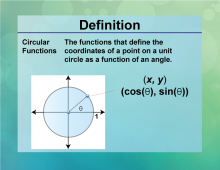
Definition--Circle Concepts--Circular Functions	Circular Functions Topic Circles Definition Circular functions are trigonometric functions that relate angles to ratios of sides in a right triangle.	Definition of a Circle
Definition--Circle Concepts--Circular Models	Circular Models Topic Circles Definition Circular models are representations of circular phenomena using mathematical equations and diagrams.	Definition of a Circle
Definition--Circle Concepts--Circular Numerical Models	Circular Numerical Models Topic Circles Definition Circular numerical models use numerical methods to analyze and simulate circular phenomena.	Definition of a Circle
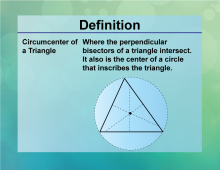
Definition--Circle Concepts--Circumcenter of Triangle	Circumcenter of Triangle Topic Circles Definition The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, equidistant from the vertices.	Definition of a Circle
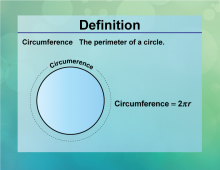
Definition--Circle Concepts--Circumference	Circumference Topic Circles Definition The circumference of a circle is the distance around the circle, calculated as C = 2πr. Description The circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr	Definition of a Circle
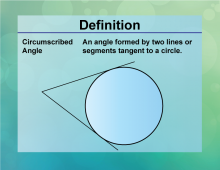
Definition--Circle Concepts--Circumscribed Angle	Circumscribed Angle Topic Circles Definition A circumscribed angle is an angle formed outside a circle by two intersecting tangents.	Definition of a Circle
Definition--Circle Concepts--Concentric Circles	Concentric Circles Topic Circles Definition Concentric circles are circles that share the same center but have different radii.	Definition of a Circle
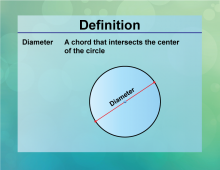
Definition--Circle Concepts--Diameter	Diameter Topic Circles Definition The diameter of a circle is a line segment that passes through the center and has its endpoints on the circle, calculated as D = 2πr. Description The diameter is a fundamental concept in geometry, representing the longest distance across a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula D = 2πr	Definition of a Circle
Definition--Circle Concepts--Equation of a Circles	Equation of a Circle Topic Circles Definition The equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius.	Definition of a Circle
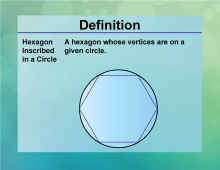
Definition--Circle Concepts--Hexagon Inscribed in a Circle	Hexagon Inscribed in a Circle Topic Circles Definition A hexagon inscribed in a circle is a six-sided polygon where each vertex touches the circle.	Definition of a Circle
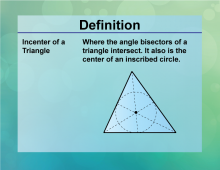
Definition--Circle Concepts--Incenter of a Triangle	Incenter of a Triangle Topic Circles Definition The incenter of a triangle is the point where the angle bisectors intersect, equidistant from the sides.	Definition of a Circle
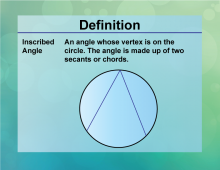
Definition--Circle Concepts--Inscribed Angle	Inscribed Angle Topic Circles Definition An inscribed angle is an angle formed by two chords in a circle that share an endpoint.	Definition of a Circle
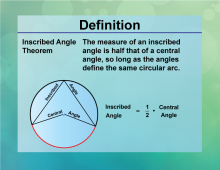
Definition--Circle Concepts--Inscribed Angle Theorem	Inscribed Angle Theorem Topic Circles Definition The inscribed angle theorem states that an inscribed angle is half the measure of the central angle that subtends the same arc.	Definition of a Circle
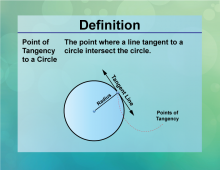
Definition--Circle Concepts--Point of Tangency to a Circle	Point of Tangency to a Circle Topic Circles Definition The point of tangency is the point where a tangent line touches the circle.	Definition of a Circle
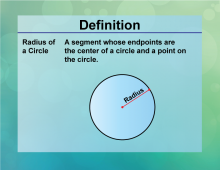
Definition--Circle Concepts--Radius of a Circle	Radius of a Circle Topic Circles Definition The radius of a circle is a line segment from the center to any point on the circle.	Definition of a Circle
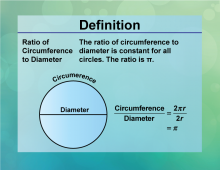
Definition--Circle Concepts--Ratio of Circumference to Diameter	Ratio of Circumference to Diameter Topic Circles Definition The ratio of the circumference to the diameter of a circle is the constant π.	Definition of a Circle
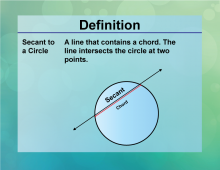
Definition--Circle Concepts--Secant to a Circle	Secant to a Circle Topic Circles Definition A secant is a line that intersects a circle at two points. Description Secants are significant in geometry, representing lines that intersect a circle at two distinct points. These lines are used in various applications, such as in design and architecture, where precise measurements of angles and distances are essential. In mathematics, secants are explored in the context of circle theorems, providing insights into the properties of lines and circles. In education, understanding secants helps students develop geometric reasoning and problem-solving skills, which are essential for advanced studies in geometry and trigonometry.	Definition of a Circle
Definition--Circle Concepts--Sector	Sector Topic Circles Definition A sector is a portion of a circle enclosed by two radii and the arc between them. Description Sectors are fundamental in the study of circles, representing a portion of the circle's area. These shapes are used in various applications, such as in design and architecture, where precise measurements of angles and areas are essential. The area of a sector is calculated using the formula A = 1/2r2θ	Definition of a Circle
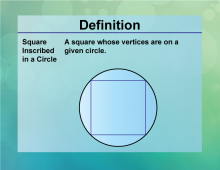
Definition--Circle Concepts--Square Inscribed in a Circle	Square Inscribed in a Circle Topic Circles Definition A square inscribed in a circle has its vertices touching the circle.	Definition of a Circle
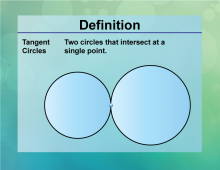
Definition--Circle Concepts--Tangent Circles	Tangent Circles Topic Circles Definition Tangent circles are two or more circles that intersect at exactly one point.	Definition of a Circle
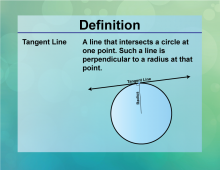
Definition--Circle Concepts--Tangent Line	Tangent Line Topic Circles Definition A tangent line is a straight line that touches a circle at exactly one point.	Definition of a Circle
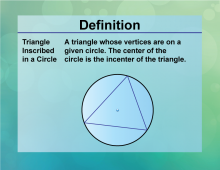
Definition--Circle Concepts--Triangle Inscribed in a Circle	Triangle Inscribed in a Circle Topic Circles Definition A triangle inscribed in a circle has its vertices on the circle.	Definition of a Circle
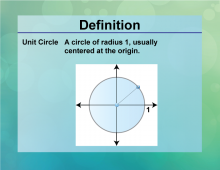
Definition--Circle Concepts--Unit Circle	Unit Circle Topic Circles Definition The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane.	Definition of a Circle
Definition--Complex Fraction	Complex Fraction Topic Fractions Definition A complex fraction is a fraction where the numerator, the denominator, or both, contain a fraction themselves. Description Complex fractions are an important concept in the study of fractions and algebra. They appear in various mathematical contexts, particularly when dealing with rational expressions and advanced algebraic operations. Understanding complex fractions is essential for simplifying expressions and solving equations that involve multiple layers of fractions.	Fractions and Mixed Numbers
Instructional Resource--Geometric Construction--Constructing an Egg Shape	Instructional Resource \| Geometric Construction \| An Egg Shape In this instructional resource, we show the steps in constructing an egg shape. In the process, students learn about using common points of tangency to create smooth curves from two different shapes. This activity can be done with pencil, compass, ruler, and grid paper. —PRESS PREVIEW TO VIEW THE ACTIVITY— To see the complete collection of Instructional Resource, click on this link.	Geometric Constructions with Circles
INSTRUCTIONAL RESOURCE: Math Examples 1	INSTRUCTIONAL RESOURCE: Math Examples--Circular Area and Circumference This set of tutorials provides 23 examples of solving for the area and circumferences of circles and sections of circles. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Area and Circumference
INSTRUCTIONAL RESOURCE: Pumpkin PI	In this Slide Show, do a hands-on geometry activity to measure π. Note: The download is a PPT file.	Ratios and Rates
Interactive Crossword Puzzle--Circles	Interactive Crossword Puzzle--Circles This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide. Related Resources To see additional resources on this topic, click on the Related Resources tab.	Definition of a Circle
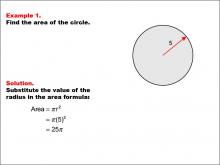
Math Example--Area and Perimeter--Circular Area and Circumference: Example 1	Math Example--Area and Perimeter--Circular Area and Circumference: Example 1 Topic Geometry Description This example presents a circle with a radius of 5 units. The task is to calculate the area of the circle using the given radius. The solution involves substituting the radius value into the area formula: A = π * r^2 = π * (5)^2 = 25π. Understanding circular area and circumference is integral to mastering geometry. Concepts such as calculating areas and circumferences of circles are fundamental, and exercises like these examples not only provide practice but also deepen the understanding of theoretical concepts in a practical way.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10	Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 Topic Geometry Description This example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11	Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 Topic Geometry Description This example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π.	Area and Circumference
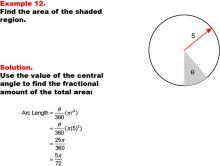
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12	Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 Topic Geometry Description This example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13	Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 Topic Geometry Description This example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π.	Area and Circumference
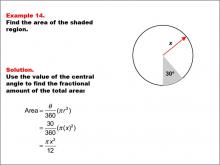
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14	Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 Topic Geometry Description This example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 15	Math Example--Area and Perimeter--Circular Area and Circumference: Example 15 Topic Geometry Description This example presents a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the arc length of the shaded region in terms of x. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * (2 * π * x) = x / 6 * π.	Area and Circumference
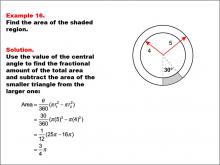
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16	Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 Topic Geometry Description This example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4.	Area and Circumference
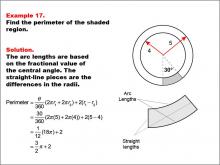
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17	Math Example--Area and Perimeter--Circular Area and Circumference: Example 17 Topic Geometry Description This example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 18	Math Example--Area and Perimeter--Circular Area and Circumference: Example 18 Topic Geometry Description This example features two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x, y, and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * y2) = (θπ / 360) * (x2 - y2).	Area and Circumference
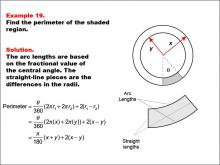
Math Example--Area and Perimeter--Circular Area and Circumference: Example 19	Math Example--Area and Perimeter--Circular Area and Circumference: Example 19 Topic Geometry Description This example presents two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x, y, and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2πx + 2πy) + 2(x - y) = π/180 * θ(x + y) + 2(x - y).	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 2	Math Example--Area and Perimeter--Circular Area and Circumference: Example 2 Topic Geometry Description This example features a circle with a radius of 5 units. The objective is to calculate the circumference of the circle using the given radius. The solution involves applying the circumference formula: C = 2 * π * r = 2 * π * (5) = 10π. Circular area and circumference calculations are fundamental in geometry. These examples provide students with practical applications of theoretical concepts, helping them understand the relationship between a circle's radius and its circumference.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 20	Math Example--Area and Perimeter--Circular Area and Circumference: Example 20 Topic Geometry Description This example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded region in terms of y. The solution involves calculating the difference between the areas of the larger and smaller circles, accounting for the central angle: Area = π/12 * (25 - y2).	Area and Circumference
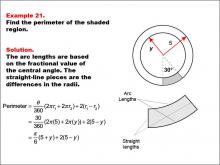
Math Example--Area and Perimeter--Circular Area and Circumference: Example 21	Math Example--Area and Perimeter--Circular Area and Circumference: Example 21 Topic Geometry Description This example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. Given a central angle of 30 degrees, radius 5, and unknown radius y, the perimeter is calculated as: Perimeter = π/6 * (5 + y) + 2(5 - y).	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 22	Math Example--Area and Perimeter--Circular Area and Circumference: Example 22 Topic Geometry Description This example presents two concentric circles with radii 4 and x, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * 42) = (θ * π / 360) * (x2 - 16).	Area and Circumference
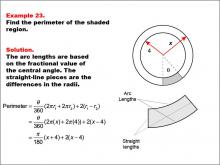
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23	Math Example--Area and Perimeter--Circular Area and Circumference: Example 23 Topic Geometry Description This example features two concentric circles with radii x and 4, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * x + 2 * π * 4) + 2 * (x - 4) = (π / 180) * θ(x + 4) + 2(x - 4).	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 3	Math Example--Area and Perimeter--Circular Area and Circumference: Example 3 Topic Geometry Description This example introduces a circle with an unknown radius represented by x. The task is to express the area of the circle in terms of x. The solution demonstrates how to use the area formula with a variable radius: A = π * r2 = π * (x)2 = π * x2. Working with variable expressions in geometry helps students transition from concrete to abstract thinking. This example bridges the gap between numerical calculations and algebraic representations, a crucial skill in advanced mathematics.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 4	Math Example--Area and Perimeter--Circular Area and Circumference: Example 4 Topic Geometry Description This example presents a circle with an unknown radius represented by x. The task is to express the circumference of the circle in terms of x. The solution demonstrates how to use the circumference formula with a variable radius: C = 2 * π * r = 2 * π * x = 2πx. Understanding circular area and circumference is crucial in geometry. This example helps students transition from concrete numerical values to abstract algebraic expressions, fostering a deeper comprehension of the relationship between a circle's radius and its circumference.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 5	Math Example--Area and Perimeter--Circular Area and Circumference: Example 5 Topic Geometry Description This example features two concentric circles with radii of 5 and 4 units. The task is to calculate the area of the shaded region between these circles. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * (4)2 = 25π - 16π = 9π. Concentric circles and shaded regions introduce students to more complex geometric concepts. This example builds upon basic circular area calculations, encouraging students to think about the relationships between different circles and how to find areas of composite shapes.	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6	Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 Topic Geometry Description This example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2).	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7	Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 Topic Geometry Description This example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2).	Area and Circumference
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8	Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 Topic Geometry Description This example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12.	Area and Circumference