
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 9: Measurement Error (Part 2)
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
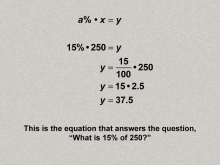
|
Math Clip Art--Ratios, Proportions, Percents--Percents 12 | Math Clip Art--Ratios, Proportions, Percents--Percents 12TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of how to solve the question 'what is 15% of 250?' using the equation a% * x = y, with calculations explicitly shown as 15 * 2.5 = 37.5. and expands on this idea by showing that provides a clear, step-by-step example to apply the general percent equation, enhancing comprehension through practical application. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Percents 13 | Math Clip Art--Ratios, Proportions, Percents--Percents 13TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of solving '150 is 30% of what number?' using the same equation a% * x = y and algebraic manipulation to find x = 500 and expands on this idea by showing that explains how to rearrange the percent equation to solve for different variables, expanding on problem-solving strategies. |
Percents |
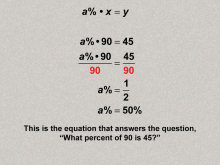
|
Math Clip Art--Ratios, Proportions, Percents--Percents 14 | Math Clip Art--Ratios, Proportions, Percents--Percents 14TopicRatios, Proportions, and Percents DescriptionThe image illustrates solving the problem 'what percent of 90 is 45?' using the equation a% * x = y, and algebraically finding a% = 50% and expands on this idea by showing that demonstrates how to find the percent in percent equations, further developing flexibility in solving percent-related problems. |
Percents |

|
Math Clip Art--Ratios, Proportions, Percents--Percents 15 | Math Clip Art--Ratios, Proportions, Percents--Percents 15TopicRatios, Proportions, and Percents DescriptionThe image summarizes the three types of percent equations in a table format, highlighting the unknown variable in each scenario (percent, part, or whole) and expands on this idea by providing a comprehensive overview and categorization of percent problems, solidifying the framework introduced in earlier examples. |
Percents |

|
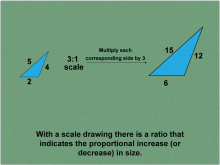
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
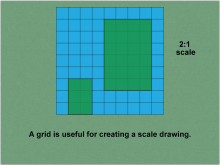
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 1 | Math Example--Area and Perimeter--Quadrilaterals: Example 1TopicGeometry DescriptionThis example demonstrates how to calculate the area of a square. The square ABCD has sides measuring 3 units each. To find the area, we use the formula A = s², where s is the length of a side. In this case, A = 3² = 9 square units. Understanding area and perimeter of quadrilaterals is a fundamental concept in geometry. This collection of examples helps students grasp these concepts by providing visual representations and step-by-step calculations for various quadrilaterals. By exploring different shapes and sizes, students develop a deeper understanding of how dimensions relate to area and perimeter. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 10 | Math Example--Area and Perimeter--Quadrilaterals: Example 10TopicGeometry DescriptionThis example demonstrates the calculation of a rhombus's area using algebraic expressions. The rhombus has a base of x + 6 units and a height of x - 2 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 6)(x - 2) = x² + 4x - 12 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 11 | Math Example--Area and Perimeter--Quadrilaterals: Example 11TopicGeometry DescriptionThis example illustrates how to calculate the area of a kite using its diagonals. The kite has diagonals measuring 25 units and 19 units. To find the area of a kite, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = (25 × 19) ÷ 2 = 475 ÷ 2 = 237.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 12 | Math Example--Area and Perimeter--Quadrilaterals: Example 12TopicGeometry DescriptionThis example demonstrates the calculation of a kite's area using algebraic expressions for its diagonals. The kite has diagonals measuring x + 11 units and x - 5 units. To find the area, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = [(x + 11)(x - 5)] ÷ 2 = (x² + 6x - 55) ÷ 2 = ½x² + 3x - 27.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 13 | Math Example--Area and Perimeter--Quadrilaterals: Example 13TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a square. The square ABCD has sides measuring 6 units each. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 6 = 24 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 14 | Math Example--Area and Perimeter--Quadrilaterals: Example 14TopicGeometry DescriptionThis example illustrates the calculation of a square's perimeter using an algebraic expression. The square ABCD has sides measuring x + 15 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 15) = 4x + 60 units. Incorporating algebra into geometry problems helps students connect different mathematical concepts and develop more advanced problem-solving skills. This collection of examples bridges the gap between basic geometry and algebraic thinking, preparing students for more complex mathematical challenges they will encounter in higher-level courses. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 15 | Math Example--Area and Perimeter--Quadrilaterals: Example 15TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rectangle. The rectangle ABCD has a length of 18 units and a width of 12 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2(18 + 12) = 2(30) = 60 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 16 | Math Example--Area and Perimeter--Quadrilaterals: Example 16TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's perimeter using algebraic expressions. The rectangle ABCD has a length of x + 25 units and a width of x - 7 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2[(x + 25) + (x - 7)] = 2(2x + 18) = 4x + 36 units. |
Area and Perimeter of Quadrilaterals |
|
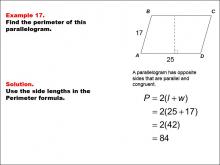
Math Example--Area and Perimeter--Quadrilaterals: Example 17 | Math Example--Area and Perimeter--Quadrilaterals: Example 17TopicGeometry DescriptionThis example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units. |
Area and Perimeter of Quadrilaterals |
|
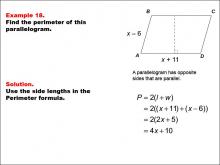
Math Example--Area and Perimeter--Quadrilaterals: Example 18 | Math Example--Area and Perimeter--Quadrilaterals: Example 18TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 19 | Math Example--Area and Perimeter--Quadrilaterals: Example 19TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 2 | Math Example--Area and Perimeter--Quadrilaterals: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units. Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 20 | Math Example--Area and Perimeter--Quadrilaterals: Example 20TopicGeometry DescriptionThis example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 21 | Math Example--Area and Perimeter--Quadrilaterals: Example 21TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 22 | Math Example--Area and Perimeter--Quadrilaterals: Example 22TopicGeometry DescriptionThis example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 23 | Math Example--Area and Perimeter--Quadrilaterals: Example 23TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a kite. The kite ABCD has two pairs of equal sides: AB and AD measure 22 units each, while BC and CD measure 11 units each. To find the perimeter, we add all four side lengths. In this case, P = 22 + 22 + 11 + 11 = 66 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 24 | Math Example--Area and Perimeter--Quadrilaterals: Example 24TopicGeometry DescriptionThis example illustrates the calculation of a kite's perimeter using algebraic expressions. The kite ABCD has two pairs of equal sides: AB and AD measure x + 11 units each, while BC and CD measure x - 5 units each. To find the perimeter, we add all four side lengths. In this case, P = (x + 11) + (x + 11) + (x - 5) + (x - 5) = 4x + 12 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 3 | Math Example--Area and Perimeter--Quadrilaterals: Example 3TopicGeometry DescriptionThis example demonstrates how to calculate the area of a rectangle. The rectangle ABCD has a length of 12 units and a width of 8 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = 12 × 8 = 96 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 4 | Math Example--Area and Perimeter--Quadrilaterals: Example 4TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's area using algebraic expressions. The rectangle ABCD has a length of x + 10 units and a width of x - 3 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = (x + 10)(x - 3) = x² + 7x - 30 square units. |
Area and Perimeter of Quadrilaterals |
|
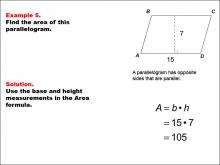
Math Example--Area and Perimeter--Quadrilaterals: Example 5 | Math Example--Area and Perimeter--Quadrilaterals: Example 5TopicGeometry DescriptionThis example illustrates how to calculate the area of a parallelogram. The parallelogram ABCD has a base of 15 units and a height of 7 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 15 × 7 = 105 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 6 | Math Example--Area and Perimeter--Quadrilaterals: Example 6TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's area using algebraic expressions. The parallelogram ABCD has a base of x + 9 units and a height of x - 4 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 9)(x - 4) = x² + 5x - 36 square units. |
Area and Perimeter of Quadrilaterals |
|
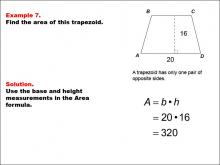
Math Example--Area and Perimeter--Quadrilaterals: Example 7 | Math Example--Area and Perimeter--Quadrilaterals: Example 7TopicGeometry DescriptionThis example illustrates how to calculate the area of a trapezoid. The trapezoid ABCD has a base of 20 units and a height of 16 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 20 × 16 = 320 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 8 | Math Example--Area and Perimeter--Quadrilaterals: Example 8TopicGeometry DescriptionThis example demonstrates the calculation of a trapezoid's area using algebraic expressions. The trapezoid ABCD has a base of x + 12 units and a height of x - 5 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 12)(x - 5) = x² + 7x - 60 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 9 | Math Example--Area and Perimeter--Quadrilaterals: Example 9TopicGeometry DescriptionThis example illustrates how to calculate the area of a rhombus. The rhombus ABCD has a side length of 25 units and a height (perpendicular distance between parallel sides) of 19 units. To find the area, we use the formula A = b × h, where b is the base (which is the same as the side length in a rhombus) and h is the height. In this case, A = 25 × 19 = 475 square units. |
Area and Perimeter of Quadrilaterals |
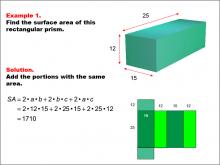
|
Math Example--Area and Perimeter--Surface Area: Example 1 | Math Example--Area and Perimeter--Surface Area: Example 1TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular prism. The prism has dimensions of 25, 15, and 12 units. The surface area is determined by summing the areas of all faces, which is represented by the formula SA = 2ab + 2bc + 2ac. For this specific prism, the calculation yields a surface area of 1710 square units. |
Surface Area |
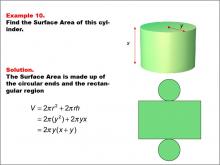
|
Math Example--Area and Perimeter--Surface Area: Example 10 | Math Example--Area and Perimeter--Surface Area: Example 10TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cylinder with radius y and height x. The surface area consists of two circular ends and the rectangular region forming the curved surface. The formula used is SA = 2πr2 + 2πrh, which simplifies to SA = 2πy(x + y), where y is the radius and x is the height of the cylinder. |
Surface Area |
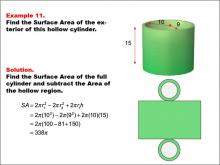
|
Math Example--Area and Perimeter--Surface Area: Example 11 | Math Example--Area and Perimeter--Surface Area: Example 11TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The surface area is determined by subtracting the area of the hollow region from the full cylinder's surface area. The formula used is SA = 2πr12 - 2πr22 + 2πr1h, where r1 is the outer radius and r2 is the inner radius. For this specific hollow cylinder, the calculation yields a surface area of 338π square units. |
Surface Area |
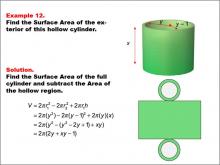
|
Math Example--Area and Perimeter--Surface Area: Example 12 | Math Example--Area and Perimeter--Surface Area: Example 12TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow cylinder with an outer radius y, an inner radius y - 1, and a height x. The surface area is determined by subtracting the hollow region's area from the full cylinder's surface area. The formula used is SA = 2πr12 - 2πr22 + 2πr1h, which simplifies to SA = 2π(2y + xy - 1), where r1 is the outer radius (y) and r2 is the inner radius (y - 1). |
Surface Area |
|
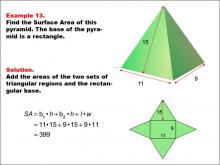
Math Example--Area and Perimeter--Surface Area: Example 13 | Math Example--Area and Perimeter--Surface Area: Example 13TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular-based pyramid with dimensions 11, 9, and 15 units. The pyramid is depicted with its net unfolded, showing two triangular faces and a rectangular base. The surface area is calculated using the formula SA = b1 * h + b2 * h + l * w, where b1 and b2 are the bases of the triangular faces, h is the height of the triangular faces, and l and w are the length and width of the rectangular base. For this specific pyramid, the calculation yields a surface area of 399 square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 14 | Math Example--Area and Perimeter--Surface Area: Example 14TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a rectangular-based pyramid with dimensions labeled as x, y, and z. The pyramid is depicted with its net unfolded into two triangular faces and one rectangular base. The surface area is calculated using the formula SA = b1 * h + b2 * h + l * w, which simplifies to SA = xz + yz + xy, where x and y are the dimensions of the rectangular base, and z is the height of the triangular faces. |
Surface Area |
|
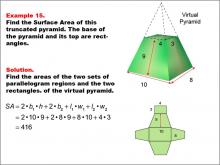
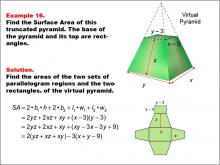
Math Example--Area and Perimeter--Surface Area: Example 15 | Math Example--Area and Perimeter--Surface Area: Example 15TopicSurface Area |
Surface Area |
|
Math Example--Area and Perimeter--Surface Area: Example 16 | Math Example--Area and Perimeter--Surface Area: Example 16TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a truncated rectangular-based pyramid with dimensions labeled as x - 3, y - 3, z, x, and y. The virtual pyramid is shown with its net unfolded into four parallelogram regions and two rectangles. The surface area is calculated using the formula SA = 2yz + 2xz + xy + (x - 3)(y - 3), which simplifies to SA = (yz + xz + xy) - (x + y - 9). |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 17 | Math Example--Area and Perimeter--Surface Area: Example 17TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a sphere with a radius of 3 units. The surface area is calculated using the formula SA = 4πr2, where r is the radius of the sphere. For this specific sphere, the calculation yields a surface area of 36π square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 18 | Math Example--Area and Perimeter--Surface Area: Example 18TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a sphere with an unknown radius labeled as "x". The surface area is calculated using the formula SA = 4πr2, which in this case becomes SA = 4πx2, where x is the radius of the sphere. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 19 | Math Example--Area and Perimeter--Surface Area: Example 19TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cube with a side length of 7 units. The surface area is calculated using the formula SA = 6s2, where s is the length of one side of the cube. For this specific cube, the calculation yields a surface area of 294 square units. |
Surface Area |
|
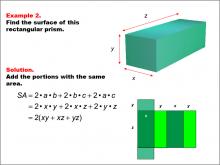
Math Example--Area and Perimeter--Surface Area: Example 2 | Math Example--Area and Perimeter--Surface Area: Example 2TopicSurface Area DescriptionThis example introduces a general formula for calculating the surface area of a rectangular prism with dimensions x, y, and z. The surface area is computed using the formula SA = 2xy + 2xz + 2yz, which can be simplified to 2(xy + xz + yz). This generalized approach allows for easy application to prisms of various sizes. Surface area calculations are fundamental in mathematics, with applications ranging from manufacturing to environmental science. This collection of examples aids in teaching the topic by presenting both specific and general cases, helping students understand how to apply formulas flexibly to different scenarios. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 20 | Math Example--Area and Perimeter--Surface Area: Example 20TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cube with an unknown side length labeled as "x". The surface area is calculated using the formula SA = 6s2, which in this case becomes SA = 6x2, where x is the length of one side of the cube. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 21 | Math Example--Area and Perimeter--Surface Area: Example 21TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow cube with an outer side length of 9 units and an inner hollow square side length of 7 units. The surface area is calculated using the formula SA = 6 * s12 - 2 * s22, where s1 is the outer side length and s2 is the inner side length. For this specific hollow cube, the calculation yields a surface area of 388 square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 22 | Math Example--Area and Perimeter--Surface Area: Example 22TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow cube with variable dimensions. The outer side length is labeled as "x" and the inner hollow side length as "x - 2". The surface area is calculated using the formula SA = 6 * s12 - 2 * s22, where s1 = x and s2 = x - 2. After expanding and simplifying, the result is SA = 4(x2 + 2x - 2) square units. |
Surface Area |
|
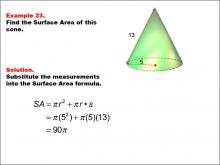
Math Example--Area and Perimeter--Surface Area: Example 23 | Math Example--Area and Perimeter--Surface Area: Example 23TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cone with a radius of 5 units and a slant height of 13 units. The surface area is calculated using the formula SA = π * r2 + π * r * s, where r is the radius and s is the slant height. For this specific cone, the calculation yields a surface area of 90π square units. |
Surface Area |