
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 14: Using Linear Relations to Solve Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Closed Captioned Video: Algebra Applications: Linear Functions, 3 | Closed Captioned Video: Algebra Applications: Linear Functions, 3TopicLinear Functions DescriptionUses linear regression to analyze US oil consumption trends, projecting future usage and potential impact of Alaskan oil production. This video explores the mathematics behind Linear Functions, providing clear examples and engaging visuals to enhance understanding. It is an excellent resource for both introduction and reinforcement of key concepts. |
Special Functions and Applications of Linear Functions |

|
Closed Captioned Video: Algebra Applications: Linear Functions, 4 | Closed Captioned Video: Algebra Applications: Linear Functions, 4TopicLinear Functions DescriptionModels maximum heart rate during aerobic exercise with linear equations, creating exercise charts for various age groups. This video explores the mathematics behind Linear Functions, providing clear examples and engaging visuals to enhance understanding. It is an excellent resource for both introduction and reinforcement of key concepts. |
Special Functions and Applications of Linear Functions |

|
Closed Captioned Video: Algebra Applications: Systems of Equations | Closed Captioned Video: Algebra Applications: Systems of EquationsTopicSystems of Equations |
Applications of Linear Systems and Solving Systems of Equations |

|
Closed Captioned Video: Algebra Applications: Systems of Equations, 1 | Closed Captioned Video: Algebra Applications: Systems of Equations, 1TopicSystems of Equations DescriptionExplores profit and loss through linear functions, focusing on break-even points and business profitability using TI-Nspire for visualizations. This video demonstrates the mathematical principles of Systems of Equations through practical applications. By focusing on real-world scenarios, it provides a unique lens to understand the interplay of mathematical models and their uses in problem-solving. |
Applications of Linear Systems and Solving Systems of Equations |

|
Closed Captioned Video: Algebra Applications: Systems of Equations, 2 | Closed Captioned Video: Algebra Applications: Systems of Equations, 2TopicSystems of Equations DescriptionDiscusses encryption using linear systems, demonstrating substitution ciphers and matrix-based encoding for secure communication. This video demonstrates the mathematical principles of Systems of Equations through practical applications. By focusing on real-world scenarios, it provides a unique lens to understand the interplay of mathematical models and their uses in problem-solving. |
Applications of Linear Systems and Solving Systems of Equations |

|
Closed Captioned Video: Algebra Applications: Systems of Equations, 3 | Closed Captioned Video: Algebra Applications: Systems of Equations, 3TopicSystems of Equations DescriptionAnalyzes ballistic missile interception through quadratic systems, graphing missile paths and their intersection as solutions to equations. This video demonstrates the mathematical principles of Systems of Equations through practical applications. By focusing on real-world scenarios, it provides a unique lens to understand the interplay of mathematical models and their uses in problem-solving. |
Applications of Linear Systems and Solving Systems of Equations |

|
Closed Captioned Video: Algebra Nspirations: Functions and Relations | Closed Captioned Video: Algebra Nspirations: Functions and Relations
Functions are relationships between quantities that change. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video explores the definition of a function, its vocabulary and notations, and distinguishes the concept of function from a general relation. Multiple representations of functions are provided using the TI-Nspire, while dynamic visuals and scenarios put them into real-world contexts. Concepts explored: functions, relations, equations, quadratic functions, linear functions, multiple representations. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Nspirations: Functions and Relations, 1 | Closed Captioned Video: Algebra Nspirations: Functions and Relations, Segment 1
In this Investigation we explore the definition of a Relation. This video is Segment 1 of a 4 segment series related to Functions and Relations. Segments 1 and 2 are grouped together. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Nspirations: Functions and Relations, 3 | Closed Captioned Video: Algebra Nspirations: Functions and Relations, Segment 3
In this Investigation we look at functions. This video is Segment 3 of a 4 segment series related to Functions and Relations. Segments 3 and 4 are grouped together. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Nspirations: Linear Functions | Closed Captioned Video: Algebra Nspirations: Linear Functions
In this program, internationally acclaimed mathematics educator Dr. Monica Neagoy, explores the nature of linear functions through the use TI graphing calculators. Examples ranging from air travel, construction, engineering, and space travel provide real-world examples for discovering algebraic concepts. All examples are solved algebraically and then reinforced through the use of the TI-Nspire. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series. Concepts explored: Standard form, slope-intercept form, point-slope form, solving linear equations. |
Applications of Linear Functions |

|
Closed Captioned Video: Algebra Nspirations: Linear Functions, 1 | Closed Captioned Video: Algebra Nspirations: Linear Functions, Segment 1
In this Investigation we look at linear models for objects moving at a constant speed. This video is Segment 1 of a 4 segment series related to Algebra Nspirations: Linear Functions. Segments 1 and 2 are grouped together. |
Applications of Linear Functions |

|
Closed Captioned Video: Algebra Nspirations: Linear Functions, 3 | Closed Captioned Video: Algebra Nspirations: Linear Functions, Segment 3
In this Investigation we look at a linear regression for carbon dioxide emission data. This video is Segment 3 of a 4 segment series related to Algebra Nspirations: Linear Functions. Segments 3 and 4 are grouped together. |
Applications of Linear Functions |

|
Closed Captioned Video: Algebra Nspirations: Solving Systems of Equations | Closed Captioned Video: Algebra Nspirations: Solving Systems of Equations
Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video introduces students to systems of linear equations in two or three unknowns. To solve these systems, the host illustrates a variety of methods: four involve the TI-Nspire (spreadsheet, graphs and geometry, matrices and nSolve) and two are the classic algebraic methods known as substitution and elimination, also called the linear combinations method. The video ends with a summary of the three possible types of solutions. Concepts explored: equations, linear equations, linear systems. |
Applications of Linear Systems and Solving Systems of Equations |

|
Closed Captioned Video: Algebra Nspirations: Solving Systems of Equations, 1 | Closed Captioned Video: Algebra Nspirations: Solving Systems of Equations, Segment 1
In this Investigation we solve a linear system. This video is Segment 1 of a 4 segment series related to Algebra Nspirations: Solving Systems of Equations. Segments 1 and 2 are grouped together. |
Applications of Linear Systems and Solving Systems of Equations |

|
Closed Captioned Video: Algebra Nspirations: Solving Systems of Equations, 3 | Closed Captioned Video: Algebra Nspirations: Solving Systems of Equations, Segment 3
In this Investigation we use matrices and the elimination method to solve a linear system. This video is Segment 3 of a 4 segment series related to Algebra Nspirations: Solving Systems of Equations. Segments 3 and 4 are grouped together. |
Applications of Linear Systems and Solving Systems of Equations |

|
Closed Captioned Video: Linear Functions: Negative Slope, Negative y-Intercept | Closed Captioned Video: Linear Functions: Negative Slope, Negative y-Intercept
Video Tutorial: Linear Functions: Negative Slope, Negative y-Intercept. In this video tutorial, students learn the basics of linear functions in slope-intercept form. In particular, look at the case of a linear function with a negative slope and a negative y-intercept. |
Graphs of Linear Functions |

|
Closed Captioned Video: Linear Functions: Negative Slope, Positive y-Intercept | Closed Captioned Video: Linear Functions: Negative Slope, Positive y-Intercept
Video Tutorial: Linear Functions: Negative Slope, Positive y-Intercept. In this video tutorial, students learn the basics of linear functions in slope-intercept form. In particular, look at the case of a linear function with a negative slope and a positive y-intercept. |
Graphs of Linear Functions |

|
Closed Captioned Video: Linear Functions: Negative Slope, Zero y-Intercept | Closed Captioned Video: Linear Functions: Negative Slope, Zero y-Intercept
Video Tutorial: Linear Functions: Negative Slope, Zero y-Intercept. In this video tutorial, students learn the basics of linear functions in slope-intercept form. In particular, look at the case of a linear function with a negative slope and a zero y-intercept. |
Graphs of Linear Functions |

|
Closed Captioned Video: Linear Functions: Positive Slope, Negative y-Intercept | Closed Captioned Video: Linear Functions: Positive Slope, Negative y-Intercept
Video Tutorial: Linear Functions: Positive Slope, Negative y-Intercept. In this video tutorial, students learn the basics of linear functions in slope-intercept form. In particular, look at the case of a linear function with a positive slope and a negative y-intercept. |
Graphs of Linear Functions |

|
Closed Captioned Video: Linear Functions: Positive Slope, Positive y-Intercept | Closed Captioned Video: Linear Functions: Positive Slope, Positive y-Intercept
Video Tutorial: Linear Functions: Positive Slope, Positive y-Intercept. In this video tutorial, students learn the basics of linear functions in slope-intercept form. In particular, look at the case of a linear function with a positive slope and a positive y-intercept. |
Graphs of Linear Functions |

|
Closed Captioned Video: Linear Functions: Positive Slope, Zero y-Intercept | Closed Captioned Video: Linear Functions: Positive Slope, Zero y-Intercept
Video Tutorial: Linear Functions: Positive Slope, Zero y-Intercept. In this video tutorial, students learn the basics of linear functions in slope-intercept form. In particular, look at the case of a linear function with a positive slope and a zero y-intercept. |
Graphs of Linear Functions |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant I | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant ITopicSlope DescriptionThe video covers finding a negative slope in Quadrant I using the slope formula. It defines rise over run and demonstrates calculations using points (7, 3) and (5, 7), resulting in a slope of -2. Important terms include numerator, denominator, and coordinates. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant II | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IITopicSlope DescriptionExplains finding a negative slope in Quadrant II using the slope formula. Demonstrates with points (-1, 4) and (-7, 6), resulting in a slope of -1/3. Covers key concepts like rise over run and coordinate differences. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant III | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IIITopicSlope DescriptionThe video discusses finding a negative slope in Quadrant III using the slope formula. Points (-2, -7) and (-6, -5) result in a slope of -1/2. Highlights include simplifying coordinate differences and using the formula. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IVTopicSlope DescriptionDemonstrates calculating a negative slope in Quadrant IV. Example points are (9, -3) and (3, -1), with a slope of -1/3. Discusses coordinate differences and formula application. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and IITopicSlope DescriptionThe video discusses a negative slope with points in Quadrants I and II. Using (4, 2) and (-2, 8), it calculates a slope of -1. Highlights include rise over run and coordinate simplifications. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionExplains calculating a negative slope for points in Quadrants III and IV. Example points (7, -5) and (-5, -1) yield a slope of -1/3. Key topics include applying the slope formula and simplifying results. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant I | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant ITopicSlope DescriptionThis video explains the slope formula and applies it to find the positive slope of a line in Quadrant I. Key concepts include rise over run and calculating differences in coordinates. The example uses points (2, 3) and (6, 7) with the slope calculated as 1. Vocabulary includes rise, run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IITopicSlope DescriptionThis tutorial focuses on a positive slope in Quadrant II. Key topics include calculating slope as rise over run and using coordinate differences. It provides an example with points (-5, 4) and (-3, 8) resulting in a slope of 2. Vocabulary includes numerator, denominator, and difference. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant III | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IIITopicSlope DescriptionShows how to calculate a positive slope in Quadrant III using the slope formula. Example uses points (-3, -8) and (-2, -2), with a slope of 6. Concepts include rise over run and simplifying fractions. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IVTopicSlope DescriptionExplains finding a positive slope in Quadrant IV. Demonstrates using points (2, -5) and (4, -1) to calculate a slope of 2. Vocabulary includes rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and IITopicSlope DescriptionCovers a positive slope with points spanning Quadrants I and II. Example uses (-3, 3) and (3, 6), yielding a slope of 1/2. Discusses rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionThis video demonstrates finding a positive slope with points in Quadrants III and IV. Using points (-5, -9) and (3, -5), it calculates a slope of 1/2. Concepts covered include rise over run and simplifying coordinate differences. |
Slope |

|
Closed Captioned Video: Solving a System | Closed Captioned Video: Solving a System
In this TI Nspire tutorial for the TI-Nspire CAS, the Calculator Window is used to solve a linear system. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . This is part of a collection of closed captioned videos on various math topics. To see the complete collection of the videos, click on this link. Note: The download is Media4Math's guide to closed captioned videos.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Video TranscriptsThis video has a transcript available. To see the complete collection of video transcripts, click on this link. |
Solving Systems of Equations |

|
Definition--Direct Variation | Direct Variation
TopicLinear Functions DefinitionDirect variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. DescriptionDirect variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, 𝑘 k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering. |
Applications of Linear Functions |
|
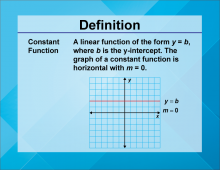
Definition--Linear Function Concepts--Constant Function | Constant Function
TopicLinear Functions DefinitionA constant function is a linear function of the form f(x) = b, where b is a constant. The graph of a constant function is a horizontal line. DescriptionConstant functions are a fundamental concept in linear functions. They represent scenarios where the output value remains unchanged, regardless of the input value. This is depicted graphically as a horizontal line, indicating that the function's rate of change is zero. In real-world applications, constant functions can model situations where a quantity remains steady over time. For example, a flat fee service charge that does not vary with usage can be represented as a constant function. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form | Converting from Standard Form to Slope-Intercept Form
TopicLinear Functions DefinitionConverting from standard form to slope-intercept form involves rewriting a linear equation from the form Ax + By = C to the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionConverting linear equations from standard form to slope-intercept form is a key skill in algebra. This conversion allows for easier graphing and interpretation of the equation's slope and y-intercept. |
Slope-Intercept Form |
|
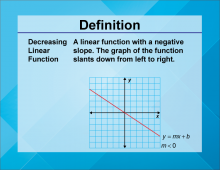
Definition--Linear Function Concepts--Decreasing Linear Function | Decreasing Linear Function
TopicLinear Functions DefinitionA decreasing linear function is a linear function where the slope is negative, indicating that as the input value increases, the output value decreases. DescriptionDecreasing linear functions are important in understanding how variables inversely relate to each other. The negative slope signifies a reduction in the dependent variable as the independent variable increases. Real-world examples include depreciation of assets over time or the decrease in temperature as altitude increases. These functions help model scenarios where an increase in one quantity results in a decrease in another. |
Slope-Intercept Form |
|
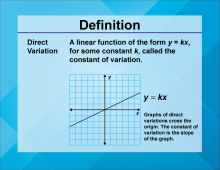
Definition--Linear Function Concepts--Direct Variation | Direct Variation
TopicLinear Functions DefinitionDirect variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. DescriptionDirect variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Equations of Parallel Lines | Equations of Parallel Lines
TopicLinear Functions DefinitionEquations of parallel lines are linear equations that have the same slope but different y-intercepts, indicating that the lines never intersect. DescriptionUnderstanding equations of parallel lines is crucial in geometry and algebra. Parallel lines have identical slopes, which means they run in the same direction and never meet. In real-world applications, parallel lines can model scenarios such as railway tracks or lanes on a highway, where maintaining a consistent distance is essential. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Equations of Perpendicular Lines | Equations of Perpendicular Lines
TopicLinear Functions DefinitionEquations of perpendicular lines are linear equations where the slopes are negative reciprocals of each other, indicating that the lines intersect at a right angle. DescriptionEquations of perpendicular lines are significant in both geometry and algebra. The negative reciprocal relationship between their slopes ensures that the lines intersect at a 90-degree angle. In real-world applications, perpendicular lines are found in various structures, such as the intersection of streets or the corners of a building, where right angles are essential. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Identity Function | Identity Function
TopicLinear Functions DefinitionAn identity function is a linear function of the form f(x) = x, where the output is equal to the input for all values of x. DescriptionThe identity function is a basic yet crucial concept in linear functions. It represents a scenario where the input value is always equal to the output value, graphically depicted as a 45-degree line passing through the origin. In real-world applications, the identity function can model situations where input and output are directly proportional and identical, such as converting units of the same measure. This also introduces the concept of identity, which is fundamental to mathematics. |
Slope-Intercept Form |
|
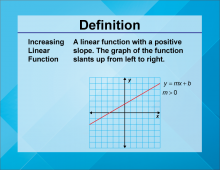
Definition--Linear Function Concepts--Increasing Linear Function | Increasing Linear Function
TopicLinear Functions DefinitionAn increasing linear function is a linear function where the slope is positive, indicating that as the input value increases, the output value also increases. DescriptionIncreasing linear functions are essential in understanding how variables positively relate to each other. The positive slope signifies an increase in the dependent variable as the independent variable increases. Real-world examples include income increasing with hours worked or the rise in temperature with the increase in daylight hours. These functions help model scenarios where an increase in one quantity results in an increase in another. |
Slope-Intercept Form |
|
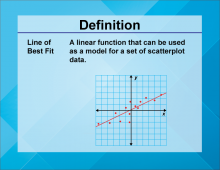
Definition--Linear Function Concepts--Line of Best Fit | Line of Best Fit
TopicLinear Functions DefinitionA line of best fit is a straight line that best represents the data on a scatter plot, showing the trend of the data points. DescriptionThe line of best fit is a crucial concept in statistics and data analysis. It helps in identifying the trend and making predictions based on the data. In real-world applications, the line of best fit is used in various fields such as economics, biology, and engineering to analyze trends and make forecasts. For example, it can be used to predict future sales based on past data. |
Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Linear Equations in Standard Form | Linear Equations in Standard Form
TopicLinear Functions DefinitionLinear equations in standard form are written as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. DescriptionLinear equations in standard form are a fundamental representation of linear functions. They provide a way to express linear relationships in a general form. |
Standard Form |
|
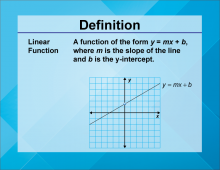
Definition--Linear Function Concepts--Linear Function | Linear Function
TopicLinear Functions DefinitionA linear function is a function that can be graphed as a straight line, typically written in the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionLinear functions are one of the most fundamental concepts in mathematics. They describe relationships where the rate of change between variables is constant, represented graphically as a straight line. This simplicity makes them a central topic in algebra and calculus. |
Slope-Intercept Form |
|
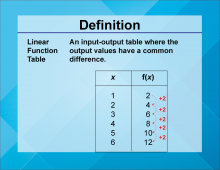
Definition--Linear Function Concepts--Linear Function Tables | Linear Function Tables
TopicLinear Functions DefinitionLinear function tables display the input-output pairs of a linear function, showing how the dependent variable changes with the independent variable. DescriptionLinear function tables are useful tools for understanding and analyzing linear relationships. They provide a clear way to see how changes in the input (independent variable) affect the output (dependent variable). |
Applications of Linear Functions and Graphs of Linear Functions |
|
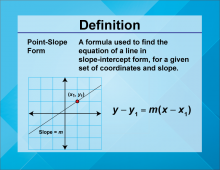
Definition--Linear Function Concepts--Point-Slope Form | Point-Slope Form
TopicLinear Functions DefinitionPoint-slope form of a linear equation is written as y − y1 = m(x−x1 ), where m is the slope and (x1 ,y1) is a point on the line. DescriptionThe point-slope form is a versatile way to express linear equations, especially useful when you know a point on the line and the slope. It allows for quick construction of the equation of a line. |
Point-Slope Form |
|
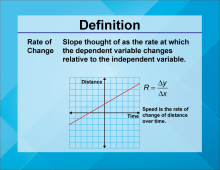
Definition--Linear Function Concepts--Rate of Change | Rate of Change
TopicLinear Functions DefinitionRate of change in a linear function is the ratio of the change in the dependent variable to the change in the independent variable, often represented as the slope m in the equation y = mx + b. DescriptionRate of change is a fundamental concept in understanding linear functions. It describes how one variable changes in relation to another, and is graphically represented by the slope of a line. |
Slope |

|
Definition--Linear Function Concepts--Slope-Intercept Form | Slope-Intercept Form
TopicLinear Functions DefinitionSlope-intercept form of a linear equation is written as y = mx + b, where m is the slope and b is the y-intercept. DescriptionSlope-intercept form is one of the most commonly used forms of linear equations. It provides a clear way to understand the slope and y-intercept of a line, making it easier to graph and interpret. In real-world applications, slope-intercept form is used in various fields such as economics, physics, and engineering to model linear relationships. For example, it can represent the relationship between cost and production levels in business. |
Slope-Intercept Form |