
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 3: Representing Proportional Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
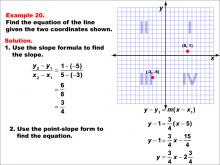
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-3, -5) and (5, 1). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (1 - (-5)) / (5 - (-3)) = 6 / 8 = 3 / 4. The point-slope form is used to find the equation: y - 1 = (3 / 4)(x - 5), resulting in y = 3/4x - 2 3/4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-3, -5) and (5, 1). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (1 - (-5)) / (5 - (-3)) = 6 / 8 = 3 / 4. The point-slope form is used to find the equation: y - 1 = (3 / 4)(x - 5), resulting in y = 3/4x - 2 3/4. |
Point-Slope Form and Slope-Intercept Form |
|
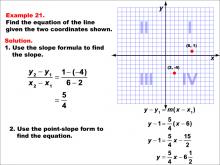
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21TopicLinear Functions DescriptionThe image shows a graph with two points (2, -4) and (6, 1) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-4)) / (6 - 2) = 5 / 4. Using point-slope form: y - 1 = (5 / 4)(x - 6), which simplifies to y = 5/4x - 6 1/2. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21TopicLinear Functions DescriptionThe image shows a graph with two points (2, -4) and (6, 1) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-4)) / (6 - 2) = 5 / 4. Using point-slope form: y - 1 = (5 / 4)(x - 6), which simplifies to y = 5/4x - 6 1/2. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21TopicLinear Functions DescriptionThe image shows a graph with two points (2, -4) and (6, 1) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-4)) / (6 - 2) = 5 / 4. Using point-slope form: y - 1 = (5 / 4)(x - 6), which simplifies to y = 5/4x - 6 1/2. |
Point-Slope Form and Slope-Intercept Form |
|
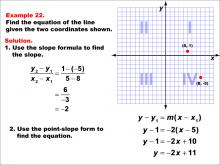
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22TopicLinear Functions DescriptionThe image shows a graph with two points (5, 1) and (8, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-5)) / (5 - 8) = -2. Using point-slope form: y - 1 = -2(x - 5), which simplifies to y = -2x + 11. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22TopicLinear Functions DescriptionThe image shows a graph with two points (5, 1) and (8, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-5)) / (5 - 8) = -2. Using point-slope form: y - 1 = -2(x - 5), which simplifies to y = -2x + 11. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22TopicLinear Functions DescriptionThe image shows a graph with two points (5, 1) and (8, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-5)) / (5 - 8) = -2. Using point-slope form: y - 1 = -2(x - 5), which simplifies to y = -2x + 11. |
Point-Slope Form and Slope-Intercept Form |
|
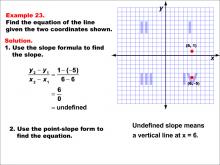
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23TopicLinear Functions DescriptionThe image shows a graph with two points (6, 1) and (6, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a vertical line using these two points. Since both x-coordinates are equal, the slope is undefined, indicating a vertical line. The slope is undefined because x-values are equal: (1 - (-5)) / (6 - 6) = undefined. This means it's a vertical line at x = 6. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23TopicLinear Functions DescriptionThe image shows a graph with two points (6, 1) and (6, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a vertical line using these two points. Since both x-coordinates are equal, the slope is undefined, indicating a vertical line. The slope is undefined because x-values are equal: (1 - (-5)) / (6 - 6) = undefined. This means it's a vertical line at x = 6. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23TopicLinear Functions DescriptionThe image shows a graph with two points (6, 1) and (6, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a vertical line using these two points. Since both x-coordinates are equal, the slope is undefined, indicating a vertical line. The slope is undefined because x-values are equal: (1 - (-5)) / (6 - 6) = undefined. This means it's a vertical line at x = 6. |
Point-Slope Form and Slope-Intercept Form |
|
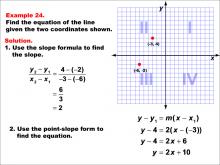
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24TopicLinear Functions DescriptionThe image shows a graph with two points (-6, -2) and (-3, 4) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (4 - (-2)) / (-3 - (-6)) = 2. Using point-slope form: y - 4 = 2(x + 3), which simplifies to y = 2x + 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24TopicLinear Functions DescriptionThe image shows a graph with two points (-6, -2) and (-3, 4) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (4 - (-2)) / (-3 - (-6)) = 2. Using point-slope form: y - 4 = 2(x + 3), which simplifies to y = 2x + 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24TopicLinear Functions DescriptionThe image shows a graph with two points (-6, -2) and (-3, 4) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (4 - (-2)) / (-3 - (-6)) = 2. Using point-slope form: y - 4 = 2(x + 3), which simplifies to y = 2x + 10. |
Point-Slope Form and Slope-Intercept Form |
|
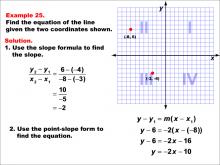
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25TopicLinear Functions DescriptionA graph with two points (-8, 6) and (-3, -4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -2x - 10. The slope is calculated as (-4 - 6) / (-3 - (-8)) = -2. Using the point-slope form y - y1 = m(x - x1), the equation becomes y - 6 = -2(x + 8), which simplifies to y = -2x - 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25TopicLinear Functions DescriptionA graph with two points (-8, 6) and (-3, -4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -2x - 10. The slope is calculated as (-4 - 6) / (-3 - (-8)) = -2. Using the point-slope form y - y1 = m(x - x1), the equation becomes y - 6 = -2(x + 8), which simplifies to y = -2x - 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25TopicLinear Functions DescriptionA graph with two points (-8, 6) and (-3, -4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -2x - 10. The slope is calculated as (-4 - 6) / (-3 - (-8)) = -2. Using the point-slope form y - y1 = m(x - x1), the equation becomes y - 6 = -2(x + 8), which simplifies to y = -2x - 10. |
Point-Slope Form and Slope-Intercept Form |
|
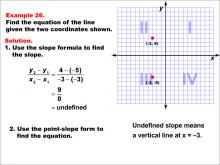
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26TopicLinear Functions DescriptionA graph with two points (-8, -6) and (4, 2) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = 1/4 x - 3. The slope is calculated as (2 + 6) / (4 + 8) = 1/4. Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 2 = 1/4(x - 4), which simplifies to y = 1/4 x - 3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26TopicLinear Functions DescriptionA graph with two points (-8, -6) and (4, 2) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = 1/4 x - 3. The slope is calculated as (2 + 6) / (4 + 8) = 1/4. Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 2 = 1/4(x - 4), which simplifies to y = 1/4 x - 3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26TopicLinear Functions DescriptionA graph with two points (-8, -6) and (4, 2) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = 1/4 x - 3. The slope is calculated as (2 + 6) / (4 + 8) = 1/4. Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 2 = 1/4(x - 4), which simplifies to y = 1/4 x - 3. |
Point-Slope Form and Slope-Intercept Form |
|
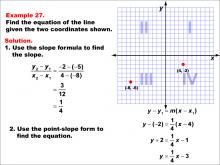
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27TopicLinear Functions DescriptionA graph with two points (-3, 4) and (-3, -5) marked on a coordinate plane. The slope is undefined because both x-coordinates are equal, leading to division by zero. This represents a vertical line at x = -3. The slope is undefined because (4 + 5) / (-3 + 3) results in division by zero. This indicates a vertical line at x = -3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27TopicLinear Functions DescriptionA graph with two points (-3, 4) and (-3, -5) marked on a coordinate plane. The slope is undefined because both x-coordinates are equal, leading to division by zero. This represents a vertical line at x = -3. The slope is undefined because (4 + 5) / (-3 + 3) results in division by zero. This indicates a vertical line at x = -3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27TopicLinear Functions DescriptionA graph with two points (-3, 4) and (-3, -5) marked on a coordinate plane. The slope is undefined because both x-coordinates are equal, leading to division by zero. This represents a vertical line at x = -3. The slope is undefined because (4 + 5) / (-3 + 3) results in division by zero. This indicates a vertical line at x = -3. |
Point-Slope Form and Slope-Intercept Form |
|
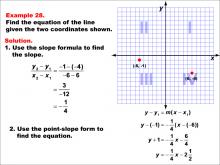
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28TopicLinear Functions DescriptionA graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2). |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28TopicLinear Functions DescriptionA graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2). |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28TopicLinear Functions DescriptionA graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2). |
Point-Slope Form and Slope-Intercept Form |
|
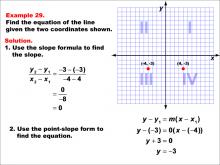
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29TopicLinear Functions |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29TopicLinear Functions |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29TopicLinear Functions |
Point-Slope Form and Slope-Intercept Form |
|
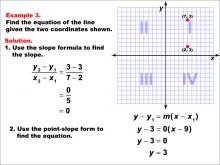
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a horizontal line passing through the points (2, 3) and (7, 3). The slope is calculated as 0 since both y-coordinates are the same. Using the point-slope form, y - y1 = m(x - x1), the equation becomes y - 3 = 0(x - any x-value), which simplifies to y = 3, representing a horizontal line. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a horizontal line passing through the points (2, 3) and (7, 3). The slope is calculated as 0 since both y-coordinates are the same. Using the point-slope form, y - y1 = m(x - x1), the equation becomes y - 3 = 0(x - any x-value), which simplifies to y = 3, representing a horizontal line. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a horizontal line passing through the points (2, 3) and (7, 3). The slope is calculated as 0 since both y-coordinates are the same. Using the point-slope form, y - y1 = m(x - x1), the equation becomes y - 3 = 0(x - any x-value), which simplifies to y = 3, representing a horizontal line. |
Point-Slope Form and Slope-Intercept Form |
|
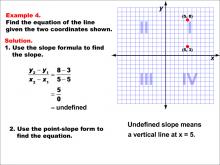
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4TopicLinear Functions DescriptionThis example illustrates how to find the equation of a vertical line passing through the points (5, 3) and (5, 8). The slope is undefined because both x-coordinates are the same, resulting in division by zero when using the slope formula. This indicates a vertical line, and the equation is simply x = 5. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4TopicLinear Functions DescriptionThis example illustrates how to find the equation of a vertical line passing through the points (5, 3) and (5, 8). The slope is undefined because both x-coordinates are the same, resulting in division by zero when using the slope formula. This indicates a vertical line, and the equation is simply x = 5. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4TopicLinear Functions DescriptionThis example illustrates how to find the equation of a vertical line passing through the points (5, 3) and (5, 8). The slope is undefined because both x-coordinates are the same, resulting in division by zero when using the slope formula. This indicates a vertical line, and the equation is simply x = 5. |
Point-Slope Form and Slope-Intercept Form |
|
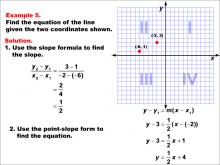
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a line passing through the points (-6, 1) and (-2, 3). The slope is calculated using the formula (y2 - y1) / (x2 - x1), resulting in a slope of 1/2. Using the point-slope form of a line, y - y1 = m(x - x1), the equation is derived and simplified to y = (1/2)x + 4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a line passing through the points (-6, 1) and (-2, 3). The slope is calculated using the formula (y2 - y1) / (x2 - x1), resulting in a slope of 1/2. Using the point-slope form of a line, y - y1 = m(x - x1), the equation is derived and simplified to y = (1/2)x + 4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a line passing through the points (-6, 1) and (-2, 3). The slope is calculated using the formula (y2 - y1) / (x2 - x1), resulting in a slope of 1/2. Using the point-slope form of a line, y - y1 = m(x - x1), the equation is derived and simplified to y = (1/2)x + 4. |
Point-Slope Form and Slope-Intercept Form |
|
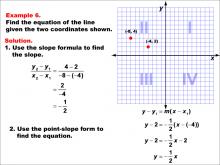
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6TopicLinear Functions DescriptionThis image shows a graph with two points (-8, 4) and (-4, 2). The slope is calculated as (y2 - y1) / (x2 - x1), resulting in a slope of -1/2. The equation of the line is derived using point-slope form and simplified to y = -(1/2)x. The slope is calculated as -1/2, and the line equation is determined using point-slope form: y = -(1/2)x. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6TopicLinear Functions DescriptionThis image shows a graph with two points (-8, 4) and (-4, 2). The slope is calculated as (y2 - y1) / (x2 - x1), resulting in a slope of -1/2. The equation of the line is derived using point-slope form and simplified to y = -(1/2)x. The slope is calculated as -1/2, and the line equation is determined using point-slope form: y = -(1/2)x. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6TopicLinear Functions DescriptionThis image shows a graph with two points (-8, 4) and (-4, 2). The slope is calculated as (y2 - y1) / (x2 - x1), resulting in a slope of -1/2. The equation of the line is derived using point-slope form and simplified to y = -(1/2)x. The slope is calculated as -1/2, and the line equation is determined using point-slope form: y = -(1/2)x. |
Point-Slope Form and Slope-Intercept Form |
|
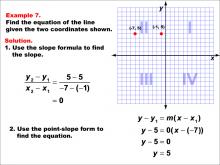
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7TopicLinear Functions DescriptionThis image shows a graph with two points (-7, 5) and (-1, 5). The slope is calculated as zero since the y-values are equal. The equation of the line is horizontal, simplified to y = 5. The slope is 0, indicating a horizontal line. The equation is y = 5. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7TopicLinear Functions DescriptionThis image shows a graph with two points (-7, 5) and (-1, 5). The slope is calculated as zero since the y-values are equal. The equation of the line is horizontal, simplified to y = 5. The slope is 0, indicating a horizontal line. The equation is y = 5. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7TopicLinear Functions DescriptionThis image shows a graph with two points (-7, 5) and (-1, 5). The slope is calculated as zero since the y-values are equal. The equation of the line is horizontal, simplified to y = 5. The slope is 0, indicating a horizontal line. The equation is y = 5. |
Point-Slope Form and Slope-Intercept Form |
|
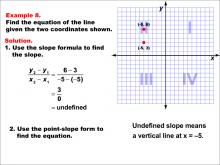
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8TopicLinear Functions DescriptionThis image shows a graph with two points (-5, 6) and (-5, 3). The slope is undefined because the x-values are equal. This results in a vertical line at x = -5. The slope is undefined, indicating a vertical line at x = -5. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8TopicLinear Functions DescriptionThis image shows a graph with two points (-5, 6) and (-5, 3). The slope is undefined because the x-values are equal. This results in a vertical line at x = -5. The slope is undefined, indicating a vertical line at x = -5. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8TopicLinear Functions DescriptionThis image shows a graph with two points (-5, 6) and (-5, 3). The slope is undefined because the x-values are equal. This results in a vertical line at x = -5. The slope is undefined, indicating a vertical line at x = -5. |
Point-Slope Form and Slope-Intercept Form |
|
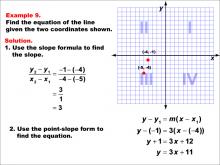
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9TopicLinear Functions DescriptionThe image shows a coordinate plane with two points (-5, -4) and (-4, -1) marked. It provides a step-by-step solution to find the equation of the line passing through these points. The slope is calculated, and the equation is derived using point-slope form. The slope is calculated as (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (-4 - (-5)) = 3 / 1 = 3. Using point-slope form, y - y1 = m(x - x1), the equation is derived as y + 1 = 3(x + 4), which simplifies to y = 3x + 11. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9TopicLinear Functions DescriptionThe image shows a coordinate plane with two points (-5, -4) and (-4, -1) marked. It provides a step-by-step solution to find the equation of the line passing through these points. The slope is calculated, and the equation is derived using point-slope form. The slope is calculated as (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (-4 - (-5)) = 3 / 1 = 3. Using point-slope form, y - y1 = m(x - x1), the equation is derived as y + 1 = 3(x + 4), which simplifies to y = 3x + 11. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9TopicLinear Functions DescriptionThe image shows a coordinate plane with two points (-5, -4) and (-4, -1) marked. It provides a step-by-step solution to find the equation of the line passing through these points. The slope is calculated, and the equation is derived using point-slope form. The slope is calculated as (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (-4 - (-5)) = 3 / 1 = 3. Using point-slope form, y - y1 = m(x - x1), the equation is derived as y + 1 = 3(x + 4), which simplifies to y = 3x + 11. |
Point-Slope Form and Slope-Intercept Form |