
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 5: Introduction to Linear Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
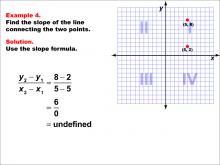
Math Example--Coordinate Geometry--Slope Formula: Example 4 | Math Example--Coordinate Geometry--Slope Formula: Example 4TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line passing through points (5, 8) and (5, 2) on a coordinate grid. When we apply the slope formula, we find that the slope is (8 - 2) / (5 - 5) = 6 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 4 | Math Example--Coordinate Geometry--Slope Formula: Example 4TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line passing through points (5, 8) and (5, 2) on a coordinate grid. When we apply the slope formula, we find that the slope is (8 - 2) / (5 - 5) = 6 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |
|
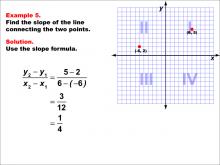
Math Example--Coordinate Geometry--Slope Formula: Example 5 | Math Example--Coordinate Geometry--Slope Formula: Example 5TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points in different quadrants: (-6, -2) in Quadrant III and (6, 5) in Quadrant I. Applying the slope formula, we find that the slope is (5 - (-2)) / (6 - (-6)) = 7 / 12 = 1 / 4. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle negative coordinates and points in different quadrants when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 5 | Math Example--Coordinate Geometry--Slope Formula: Example 5TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points in different quadrants: (-6, -2) in Quadrant III and (6, 5) in Quadrant I. Applying the slope formula, we find that the slope is (5 - (-2)) / (6 - (-6)) = 7 / 12 = 1 / 4. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle negative coordinates and points in different quadrants when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 5 | Math Example--Coordinate Geometry--Slope Formula: Example 5TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points in different quadrants: (-6, -2) in Quadrant III and (6, 5) in Quadrant I. Applying the slope formula, we find that the slope is (5 - (-2)) / (6 - (-6)) = 7 / 12 = 1 / 4. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle negative coordinates and points in different quadrants when calculating slope. |
Slope |
|
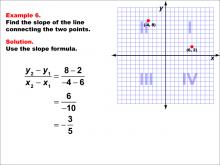
Math Example--Coordinate Geometry--Slope Formula: Example 6 | Math Example--Coordinate Geometry--Slope Formula: Example 6TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points in different quadrants: (-4, 8) in Quadrant II and (6, 2) in Quadrant I. Applying the slope formula, we find that the slope is (8 - 2) / (-4 - 6) = 6 / -10 = -3 / 5. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points in different quadrants and interpret a negative slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 6 | Math Example--Coordinate Geometry--Slope Formula: Example 6TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points in different quadrants: (-4, 8) in Quadrant II and (6, 2) in Quadrant I. Applying the slope formula, we find that the slope is (8 - 2) / (-4 - 6) = 6 / -10 = -3 / 5. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points in different quadrants and interpret a negative slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 6 | Math Example--Coordinate Geometry--Slope Formula: Example 6TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points in different quadrants: (-4, 8) in Quadrant II and (6, 2) in Quadrant I. Applying the slope formula, we find that the slope is (8 - 2) / (-4 - 6) = 6 / -10 = -3 / 5. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points in different quadrants and interpret a negative slope. |
Slope |
|
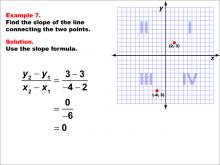
Math Example--Coordinate Geometry--Slope Formula: Example 7 | Math Example--Coordinate Geometry--Slope Formula: Example 7TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting two points: (-4, 3) in Quadrant II and (2, 3) in Quadrant I. When we apply the slope formula, we find that the slope is (3 - 3) / (-4 - 2) = 0 / -6 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero, even when the points are in different quadrants. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 7 | Math Example--Coordinate Geometry--Slope Formula: Example 7TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting two points: (-4, 3) in Quadrant II and (2, 3) in Quadrant I. When we apply the slope formula, we find that the slope is (3 - 3) / (-4 - 2) = 0 / -6 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero, even when the points are in different quadrants. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 7 | Math Example--Coordinate Geometry--Slope Formula: Example 7TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting two points: (-4, 3) in Quadrant II and (2, 3) in Quadrant I. When we apply the slope formula, we find that the slope is (3 - 3) / (-4 - 2) = 0 / -6 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero, even when the points are in different quadrants. |
Slope |
|
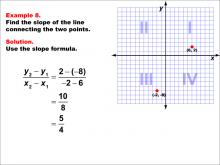
Math Example--Coordinate Geometry--Slope Formula: Example 8 | Math Example--Coordinate Geometry--Slope Formula: Example 8TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points in different quadrants: (-2, -8) in Quadrant III and (6, 2) in Quadrant I. Applying the slope formula, we find that the slope is (2 - (-8)) / (6 - (-2)) = 10 / 8 = 5 / 4. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle negative coordinates and points in different quadrants when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 8 | Math Example--Coordinate Geometry--Slope Formula: Example 8TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points in different quadrants: (-2, -8) in Quadrant III and (6, 2) in Quadrant I. Applying the slope formula, we find that the slope is (2 - (-8)) / (6 - (-2)) = 10 / 8 = 5 / 4. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle negative coordinates and points in different quadrants when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 8 | Math Example--Coordinate Geometry--Slope Formula: Example 8TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points in different quadrants: (-2, -8) in Quadrant III and (6, 2) in Quadrant I. Applying the slope formula, we find that the slope is (2 - (-8)) / (6 - (-2)) = 10 / 8 = 5 / 4. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle negative coordinates and points in different quadrants when calculating slope. |
Slope |
|
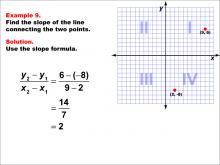
Math Example--Coordinate Geometry--Slope Formula: Example 9 | Math Example--Coordinate Geometry--Slope Formula: Example 9TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (9, 6) and (2, -8) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-8)) / (9 - 2) = 14 / 7 = 2. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 9 | Math Example--Coordinate Geometry--Slope Formula: Example 9TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (9, 6) and (2, -8) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-8)) / (9 - 2) = 14 / 7 = 2. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 9 | Math Example--Coordinate Geometry--Slope Formula: Example 9TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (9, 6) and (2, -8) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-8)) / (9 - 2) = 14 / 7 = 2. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope. |
Slope |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 1 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 1TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 7x + 1, where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 10 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 10TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 9x + (-2), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 2 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 2TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 6x + (-10), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 3 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 3TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -x + (-8), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 4 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 4TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -x + (-3), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 5 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 5TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -6x + (-3), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 6 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 6TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -3x + 1, where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 7 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 7TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -10x + (-3), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 8 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 8TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 7x + (-9), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 9 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 9TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 7x + (-3), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |
|
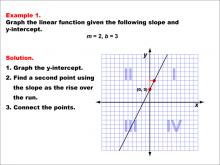
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 1 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 1TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of 2 and a y-intercept of 3. The process involves three key steps: first, plotting the y-intercept at (0, 3); second, using the slope to find another point on the line; and finally, connecting these points to form the line. |
Slope-Intercept Form |
|
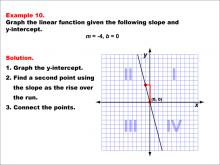
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 10 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 10TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of -4 and a y-intercept of 0. The method involves three main steps: plotting the y-intercept at the origin (0, 0), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
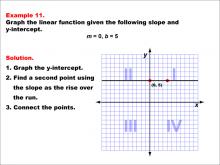
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 11 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 11TopicLinear Functions DescriptionThis example demonstrates the process of graphing a linear function with a slope of 0 and a y-intercept of 5. The procedure involves three key steps: plotting the y-intercept at (0, 5), recognizing that a slope of 0 results in a horizontal line, and drawing the line parallel to the x-axis through the y-intercept. |
Slope-Intercept Form |
|
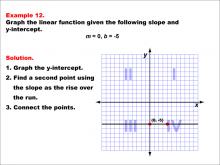
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 12 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 12TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of 0 and a y-intercept of -5. The method involves three main steps: plotting the y-intercept at (0, -5), recognizing that a slope of 0 results in a horizontal line, and drawing the line parallel to the x-axis through the y-intercept. |
Slope-Intercept Form |
|
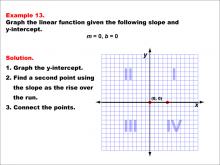
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 13 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 13TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of 0 and a y-intercept of 0. The process involves recognizing that this special case results in a horizontal line coinciding with the x-axis. The line passes through the origin (0, 0) and extends infinitely in both directions along the x-axis. |
Slope-Intercept Form |
|
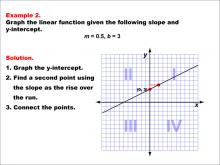
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 2 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 2TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of 0.5 and a y-intercept of 3. The method involves three main steps: plotting the y-intercept at (0, 3), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
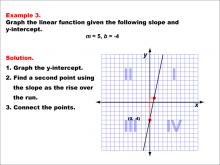
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 3 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 3TopicLinear Functions DescriptionThis example demonstrates the process of graphing a linear function with a slope of 5 and a y-intercept of -4. The procedure involves three key steps: plotting the y-intercept at (0, -4), using the slope to determine a second point on the line, and connecting these points to form the linear graph. |
Slope-Intercept Form |
|
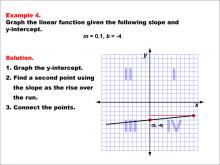
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 4 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 4TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of 0.1 and a y-intercept of -4. The method involves three main steps: plotting the y-intercept at (0, -4), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
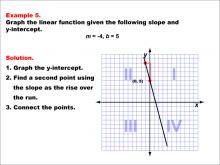
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 5 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 5TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of -4 and a y-intercept of 5. The process involves three key steps: first, plotting the y-intercept at (0, 5); second, using the slope to find another point on the line; and finally, connecting these points to form the line. |
Slope-Intercept Form |
|
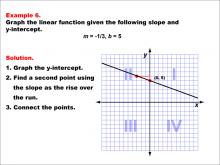
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 6 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 6TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of -1/3 and a y-intercept of 5. The method involves three main steps: plotting the y-intercept at (0, 5), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
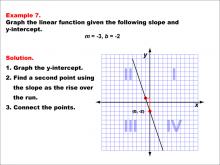
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 7 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 7TopicLinear Functions DescriptionThis example demonstrates the process of graphing a linear function with a slope of -3 and a y-intercept of -2. The procedure involves three key steps: plotting the y-intercept at (0, -2), using the slope to determine a second point on the line, and connecting these points to form the linear graph. |
Slope-Intercept Form |
|
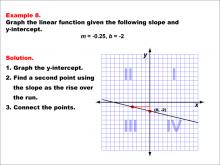
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 8 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 8TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of -0.25 and a y-intercept of -2. The method involves three main steps: plotting the y-intercept at (0, -2), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
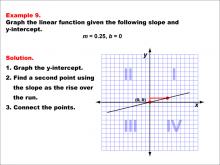
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 9 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 9TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of 0.25 and a y-intercept of 0. The process involves three key steps: first, plotting the y-intercept at the origin (0, 0); second, using the slope to find another point on the line; and finally, connecting these points to form the line. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 10 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 10TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation x + y = 1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = -x + 1. This simple transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |