
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 5: Introduction to Linear Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
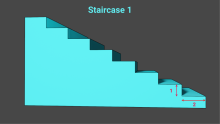
Math Clip Art: Staircase Steepness | In this set of clip art images, different values for the rise and run are given, but in all cases they result in the same slope for the staircase. These images help advance the idea that slope is a ratio and proportion. |
Slope |

|
Math Clip Art: Staircase Steepness | In this set of clip art images, different values for the rise and run are given, but in all cases they result in the same slope for the staircase. These images help advance the idea that slope is a ratio and proportion. |
Slope |

|
Math Clip Art: Types of Slope | Math Clip Art: Types of Slope Use these clip art images to show the different types of slope available. These slope types are covered: Positive SlopeNegative SlopeZero SlopeNo SlopeSlope = 1Slope =-10 < Slope < 1Slope > 1 |
Slope |

|
Math Clip Art: Types of Slope | Math Clip Art: Types of Slope Use these clip art images to show the different types of slope available. These slope types are covered: Positive SlopeNegative SlopeZero SlopeNo SlopeSlope = 1Slope =-10 < Slope < 1Slope > 1 |
Slope |
|
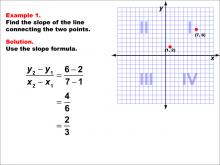
Math Example--Coordinate Geometry--Slope Formula: Example 1 | Math Example--Coordinate Geometry--Slope Formula: Example 1TopicSlope Formula DescriptionThis example demonstrates how to calculate the slope of a line connecting two points on a coordinate grid. The points (1, 2) and (7, 6) are plotted, and the slope formula is applied to find the slope between them. The calculation shows that the slope is (6 - 2) / (7 - 1) = 4 / 6 = 2 / 3. The slope formula is a fundamental concept in coordinate geometry, allowing us to determine the steepness and direction of a line. It's essential for understanding linear relationships and is widely used in various mathematical and real-world applications. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 1 | Math Example--Coordinate Geometry--Slope Formula: Example 1TopicSlope Formula DescriptionThis example demonstrates how to calculate the slope of a line connecting two points on a coordinate grid. The points (1, 2) and (7, 6) are plotted, and the slope formula is applied to find the slope between them. The calculation shows that the slope is (6 - 2) / (7 - 1) = 4 / 6 = 2 / 3. The slope formula is a fundamental concept in coordinate geometry, allowing us to determine the steepness and direction of a line. It's essential for understanding linear relationships and is widely used in various mathematical and real-world applications. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 1 | Math Example--Coordinate Geometry--Slope Formula: Example 1TopicSlope Formula DescriptionThis example demonstrates how to calculate the slope of a line connecting two points on a coordinate grid. The points (1, 2) and (7, 6) are plotted, and the slope formula is applied to find the slope between them. The calculation shows that the slope is (6 - 2) / (7 - 1) = 4 / 6 = 2 / 3. The slope formula is a fundamental concept in coordinate geometry, allowing us to determine the steepness and direction of a line. It's essential for understanding linear relationships and is widely used in various mathematical and real-world applications. |
Slope |
|
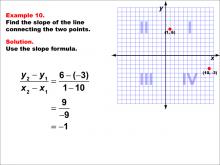
Math Example--Coordinate Geometry--Slope Formula: Example 10 | Math Example--Coordinate Geometry--Slope Formula: Example 10TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (1, 6) and (10, -3) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-3)) / (1 - 10) = 9 / -9 = -1. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 10 | Math Example--Coordinate Geometry--Slope Formula: Example 10TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (1, 6) and (10, -3) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-3)) / (1 - 10) = 9 / -9 = -1. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 10 | Math Example--Coordinate Geometry--Slope Formula: Example 10TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (1, 6) and (10, -3) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-3)) / (1 - 10) = 9 / -9 = -1. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative slope. |
Slope |
|
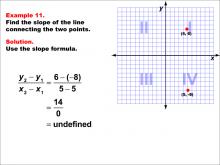
Math Example--Coordinate Geometry--Slope Formula: Example 11 | Math Example--Coordinate Geometry--Slope Formula: Example 11TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a vertical line connecting points (5, 6) and (5, -8) on a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - (-8)) / (5 - 5) = 14 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 11 | Math Example--Coordinate Geometry--Slope Formula: Example 11TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a vertical line connecting points (5, 6) and (5, -8) on a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - (-8)) / (5 - 5) = 14 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 11 | Math Example--Coordinate Geometry--Slope Formula: Example 11TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a vertical line connecting points (5, 6) and (5, -8) on a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - (-8)) / (5 - 5) = 14 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |
|
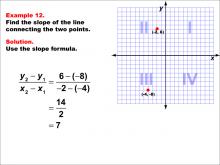
Math Example--Coordinate Geometry--Slope Formula: Example 12 | Math Example--Coordinate Geometry--Slope Formula: Example 12TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (-2, 6) and (-4, -8) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-8)) / (-2 - (-4)) = 14 / 2 = 7. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with negative coordinates when calculating slope, resulting in a positive slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 12 | Math Example--Coordinate Geometry--Slope Formula: Example 12TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (-2, 6) and (-4, -8) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-8)) / (-2 - (-4)) = 14 / 2 = 7. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with negative coordinates when calculating slope, resulting in a positive slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 12 | Math Example--Coordinate Geometry--Slope Formula: Example 12TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (-2, 6) and (-4, -8) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - (-8)) / (-2 - (-4)) = 14 / 2 = 7. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with negative coordinates when calculating slope, resulting in a positive slope. |
Slope |
|
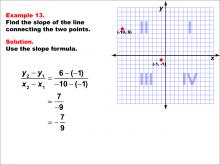
Math Example--Coordinate Geometry--Slope Formula: Example 13 | Math Example--Coordinate Geometry--Slope Formula: Example 13TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (-10, 6) and (-1, -1) on a Cartesian plane. The line crosses quadrants II and III. Applying the slope formula, we find that the slope is (6 - (-1)) / (-10 - (-1)) = 7 / -9 = -7 / 9. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points in different quadrants and with negative coordinates when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 13 | Math Example--Coordinate Geometry--Slope Formula: Example 13TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (-10, 6) and (-1, -1) on a Cartesian plane. The line crosses quadrants II and III. Applying the slope formula, we find that the slope is (6 - (-1)) / (-10 - (-1)) = 7 / -9 = -7 / 9. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points in different quadrants and with negative coordinates when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 13 | Math Example--Coordinate Geometry--Slope Formula: Example 13TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (-10, 6) and (-1, -1) on a Cartesian plane. The line crosses quadrants II and III. Applying the slope formula, we find that the slope is (6 - (-1)) / (-10 - (-1)) = 7 / -9 = -7 / 9. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points in different quadrants and with negative coordinates when calculating slope. |
Slope |
|
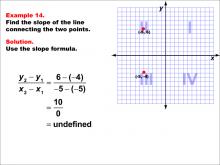
Math Example--Coordinate Geometry--Slope Formula: Example 14 | Math Example--Coordinate Geometry--Slope Formula: Example 14TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line passing through two points: (-5, 6) and (-5, -4) in Quadrant II of a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - (-4)) / (-5 - (-5)) = 10 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 14 | Math Example--Coordinate Geometry--Slope Formula: Example 14TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line passing through two points: (-5, 6) and (-5, -4) in Quadrant II of a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - (-4)) / (-5 - (-5)) = 10 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 14 | Math Example--Coordinate Geometry--Slope Formula: Example 14TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line passing through two points: (-5, 6) and (-5, -4) in Quadrant II of a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - (-4)) / (-5 - (-5)) = 10 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |
|
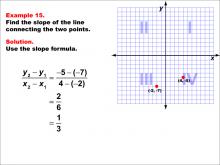
Math Example--Coordinate Geometry--Slope Formula: Example 15 | Math Example--Coordinate Geometry--Slope Formula: Example 15TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (4, -5) and (-2, -7) on a Cartesian plane. The line crosses quadrants III and IV. Applying the slope formula, we find that the slope is (-5 - (-7)) / (4 - (-2)) = 2 / 6 = 1 / 3. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with negative coordinates and in different quadrants when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 15 | Math Example--Coordinate Geometry--Slope Formula: Example 15TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (4, -5) and (-2, -7) on a Cartesian plane. The line crosses quadrants III and IV. Applying the slope formula, we find that the slope is (-5 - (-7)) / (4 - (-2)) = 2 / 6 = 1 / 3. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with negative coordinates and in different quadrants when calculating slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 15 | Math Example--Coordinate Geometry--Slope Formula: Example 15TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (4, -5) and (-2, -7) on a Cartesian plane. The line crosses quadrants III and IV. Applying the slope formula, we find that the slope is (-5 - (-7)) / (4 - (-2)) = 2 / 6 = 1 / 3. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with negative coordinates and in different quadrants when calculating slope. |
Slope |
|
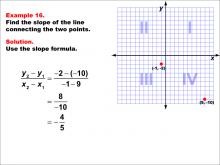
Math Example--Coordinate Geometry--Slope Formula: Example 16 | Math Example--Coordinate Geometry--Slope Formula: Example 16TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (9, -10) and (-1, -2) on a Cartesian plane. The line crosses quadrants III and IV diagonally. Applying the slope formula, we find that the slope is (-2 - (-10)) / (-1 - 9) = 8 / -10 = -4 / 5. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative fraction. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 16 | Math Example--Coordinate Geometry--Slope Formula: Example 16TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (9, -10) and (-1, -2) on a Cartesian plane. The line crosses quadrants III and IV diagonally. Applying the slope formula, we find that the slope is (-2 - (-10)) / (-1 - 9) = 8 / -10 = -4 / 5. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative fraction. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 16 | Math Example--Coordinate Geometry--Slope Formula: Example 16TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (9, -10) and (-1, -2) on a Cartesian plane. The line crosses quadrants III and IV diagonally. Applying the slope formula, we find that the slope is (-2 - (-10)) / (-1 - 9) = 8 / -10 = -4 / 5. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative fraction. |
Slope |
|
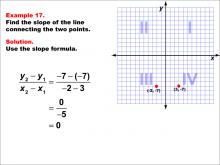
Math Example--Coordinate Geometry--Slope Formula: Example 17 | Math Example--Coordinate Geometry--Slope Formula: Example 17TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a horizontal line connecting points (-2, -7) and (3, -7) on a Cartesian plane. When we apply the slope formula, we find that the slope is (-7 - (-7)) / (-2 - 3) = 0 / -5 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero, even when the points have different x-coordinates. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 17 | Math Example--Coordinate Geometry--Slope Formula: Example 17TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a horizontal line connecting points (-2, -7) and (3, -7) on a Cartesian plane. When we apply the slope formula, we find that the slope is (-7 - (-7)) / (-2 - 3) = 0 / -5 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero, even when the points have different x-coordinates. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 17 | Math Example--Coordinate Geometry--Slope Formula: Example 17TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a horizontal line connecting points (-2, -7) and (3, -7) on a Cartesian plane. When we apply the slope formula, we find that the slope is (-7 - (-7)) / (-2 - 3) = 0 / -5 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero, even when the points have different x-coordinates. |
Slope |
|
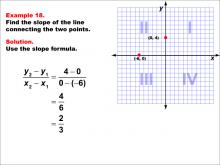
Math Example--Coordinate Geometry--Slope Formula: Example 18 | Math Example--Coordinate Geometry--Slope Formula: Example 18TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (-6, 0) and (0, 4) on a Cartesian plane. Applying the slope formula, we find that the slope is (4 - 0) / (0 - (-6)) = 4 / 6 = 2 / 3. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope, resulting in a positive fraction. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 18 | Math Example--Coordinate Geometry--Slope Formula: Example 18TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (-6, 0) and (0, 4) on a Cartesian plane. Applying the slope formula, we find that the slope is (4 - 0) / (0 - (-6)) = 4 / 6 = 2 / 3. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope, resulting in a positive fraction. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 18 | Math Example--Coordinate Geometry--Slope Formula: Example 18TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a line connecting two points: (-6, 0) and (0, 4) on a Cartesian plane. Applying the slope formula, we find that the slope is (4 - 0) / (0 - (-6)) = 4 / 6 = 2 / 3. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle points with both positive and negative coordinates when calculating slope, resulting in a positive fraction. |
Slope |
|
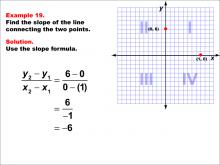
Math Example--Coordinate Geometry--Slope Formula: Example 19 | Math Example--Coordinate Geometry--Slope Formula: Example 19TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (1, 0) and (0, 6) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - 0) / (0 - 1) = 6 / -1 = -6. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative integer slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 19 | Math Example--Coordinate Geometry--Slope Formula: Example 19TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (1, 0) and (0, 6) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - 0) / (0 - 1) = 6 / -1 = -6. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative integer slope. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 19 | Math Example--Coordinate Geometry--Slope Formula: Example 19TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a line connecting two points: (1, 0) and (0, 6) on a Cartesian plane. Applying the slope formula, we find that the slope is (6 - 0) / (0 - 1) = 6 / -1 = -6. The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points with both positive and negative coordinates when calculating slope, resulting in a negative integer slope. |
Slope |
|
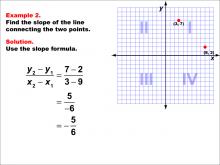
Math Example--Coordinate Geometry--Slope Formula: Example 2 | Math Example--Coordinate Geometry--Slope Formula: Example 2TopicSlope Formula DescriptionThis example illustrates the calculation of slope between two points (3, 7) and (9, 2) on a coordinate grid. The slope formula is applied to find that the slope is (7 - 2) / (3 - 9) = 5 / -6 = -5 / 6. Understanding the slope formula is crucial in coordinate geometry as it helps describe the steepness and direction of a line. This concept is widely used in various mathematical applications and real-world scenarios. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 2 | Math Example--Coordinate Geometry--Slope Formula: Example 2TopicSlope Formula DescriptionThis example illustrates the calculation of slope between two points (3, 7) and (9, 2) on a coordinate grid. The slope formula is applied to find that the slope is (7 - 2) / (3 - 9) = 5 / -6 = -5 / 6. Understanding the slope formula is crucial in coordinate geometry as it helps describe the steepness and direction of a line. This concept is widely used in various mathematical applications and real-world scenarios. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 2 | Math Example--Coordinate Geometry--Slope Formula: Example 2TopicSlope Formula DescriptionThis example illustrates the calculation of slope between two points (3, 7) and (9, 2) on a coordinate grid. The slope formula is applied to find that the slope is (7 - 2) / (3 - 9) = 5 / -6 = -5 / 6. Understanding the slope formula is crucial in coordinate geometry as it helps describe the steepness and direction of a line. This concept is widely used in various mathematical applications and real-world scenarios. |
Slope |
|
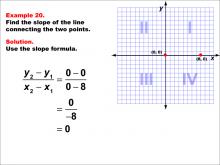
Math Example--Coordinate Geometry--Slope Formula: Example 20 | Math Example--Coordinate Geometry--Slope Formula: Example 20TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting points (0, 0) and (8, 0) on a Cartesian plane. When we apply the slope formula, we find that the slope is (0 - 0) / (8 - 0) = 0 / 8 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal and lies on the x-axis, resulting in a slope of zero. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 20 | Math Example--Coordinate Geometry--Slope Formula: Example 20TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting points (0, 0) and (8, 0) on a Cartesian plane. When we apply the slope formula, we find that the slope is (0 - 0) / (8 - 0) = 0 / 8 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal and lies on the x-axis, resulting in a slope of zero. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 20 | Math Example--Coordinate Geometry--Slope Formula: Example 20TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting points (0, 0) and (8, 0) on a Cartesian plane. When we apply the slope formula, we find that the slope is (0 - 0) / (8 - 0) = 0 / 8 = 0. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal and lies on the x-axis, resulting in a slope of zero. |
Slope |
|
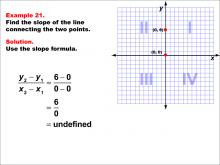
Math Example--Coordinate Geometry--Slope Formula: Example 21 | Math Example--Coordinate Geometry--Slope Formula: Example 21TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line connecting points (0, 0) and (0, 6) on a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - 0) / (0 - 0) = 6 / 0, which is undefined. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical and lies on the y-axis, resulting in an undefined slope due to division by zero. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 21 | Math Example--Coordinate Geometry--Slope Formula: Example 21TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line connecting points (0, 0) and (0, 6) on a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - 0) / (0 - 0) = 6 / 0, which is undefined. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical and lies on the y-axis, resulting in an undefined slope due to division by zero. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 21 | Math Example--Coordinate Geometry--Slope Formula: Example 21TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line connecting points (0, 0) and (0, 6) on a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - 0) / (0 - 0) = 6 / 0, which is undefined. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical and lies on the y-axis, resulting in an undefined slope due to division by zero. |
Slope |
|
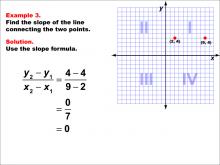
Math Example--Coordinate Geometry--Slope Formula: Example 3 | Math Example--Coordinate Geometry--Slope Formula: Example 3TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting points (2, 4) and (9, 4) on a coordinate grid. When we apply the slope formula, we find that the slope is (4 - 4) / (9 - 2) = 0 / 7 = 0. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 3 | Math Example--Coordinate Geometry--Slope Formula: Example 3TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting points (2, 4) and (9, 4) on a coordinate grid. When we apply the slope formula, we find that the slope is (4 - 4) / (9 - 2) = 0 / 7 = 0. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero. |
Slope |

|
Math Example--Coordinate Geometry--Slope Formula: Example 3 | Math Example--Coordinate Geometry--Slope Formula: Example 3TopicSlope Formula DescriptionThis example demonstrates the calculation of slope for a horizontal line connecting points (2, 4) and (9, 4) on a coordinate grid. When we apply the slope formula, we find that the slope is (4 - 4) / (9 - 2) = 0 / 7 = 0. The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal, resulting in a slope of zero. |
Slope |
|
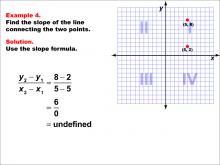
Math Example--Coordinate Geometry--Slope Formula: Example 4 | Math Example--Coordinate Geometry--Slope Formula: Example 4TopicSlope Formula DescriptionThis example illustrates the calculation of slope for a vertical line passing through points (5, 8) and (5, 2) on a coordinate grid. When we apply the slope formula, we find that the slope is (8 - 2) / (5 - 5) = 6 / 0, which is undefined. The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope. |
Slope |