
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 13: The Volume of a Cylinder
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
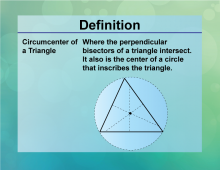
Definition--Circle Concepts--Circumcenter of Triangle | Circumcenter of TriangleTopicCircles DefinitionThe circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, equidistant from the vertices. |
Definition of a Circle |
|
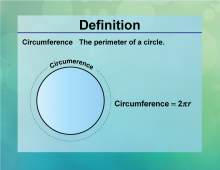
Definition--Circle Concepts--Circumference | CircumferenceTopicCircles DefinitionThe circumference of a circle is the distance around the circle, calculated as C = 2πr. DescriptionThe circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr |
Definition of a Circle |
|
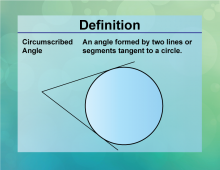
Definition--Circle Concepts--Circumscribed Angle | Circumscribed AngleTopicCircles DefinitionA circumscribed angle is an angle formed outside a circle by two intersecting tangents. |
Definition of a Circle |

|
Definition--Circle Concepts--Concentric Circles | Concentric CirclesTopicCircles DefinitionConcentric circles are circles that share the same center but have different radii. |
Definition of a Circle |
|
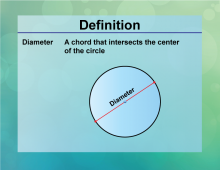
Definition--Circle Concepts--Diameter | DiameterTopicCircles DefinitionThe diameter of a circle is a line segment that passes through the center and has its endpoints on the circle, calculated as D = 2πr. DescriptionThe diameter is a fundamental concept in geometry, representing the longest distance across a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula D = 2πr |
Definition of a Circle |

|
Definition--Circle Concepts--Equation of a Circles | Equation of a CircleTopicCircles DefinitionThe equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius. |
Definition of a Circle |
|
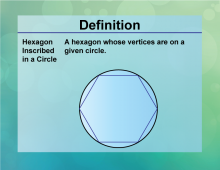
Definition--Circle Concepts--Hexagon Inscribed in a Circle | Hexagon Inscribed in a CircleTopicCircles DefinitionA hexagon inscribed in a circle is a six-sided polygon where each vertex touches the circle. |
Definition of a Circle |
|
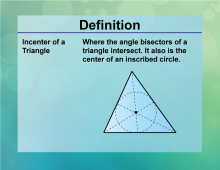
Definition--Circle Concepts--Incenter of a Triangle | Incenter of a TriangleTopicCircles DefinitionThe incenter of a triangle is the point where the angle bisectors intersect, equidistant from the sides. |
Definition of a Circle |
|
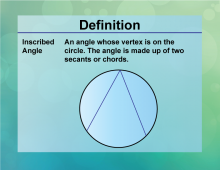
Definition--Circle Concepts--Inscribed Angle | Inscribed AngleTopicCircles DefinitionAn inscribed angle is an angle formed by two chords in a circle that share an endpoint. |
Definition of a Circle |
|
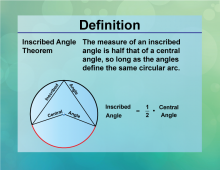
Definition--Circle Concepts--Inscribed Angle Theorem | Inscribed Angle TheoremTopicCircles DefinitionThe inscribed angle theorem states that an inscribed angle is half the measure of the central angle that subtends the same arc. |
Definition of a Circle |
|
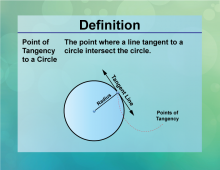
Definition--Circle Concepts--Point of Tangency to a Circle | Point of Tangency to a CircleTopicCircles DefinitionThe point of tangency is the point where a tangent line touches the circle. |
Definition of a Circle |
|
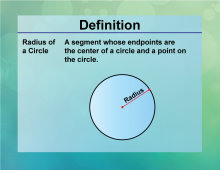
Definition--Circle Concepts--Radius of a Circle | Radius of a CircleTopicCircles DefinitionThe radius of a circle is a line segment from the center to any point on the circle. |
Definition of a Circle |
|
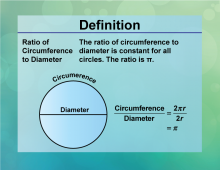
Definition--Circle Concepts--Ratio of Circumference to Diameter | Ratio of Circumference to DiameterTopicCircles DefinitionThe ratio of the circumference to the diameter of a circle is the constant π. |
Definition of a Circle |
|
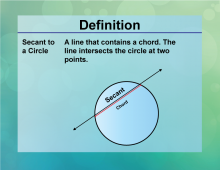
Definition--Circle Concepts--Secant to a Circle | Secant to a CircleTopicCircles DefinitionA secant is a line that intersects a circle at two points. DescriptionSecants are significant in geometry, representing lines that intersect a circle at two distinct points. These lines are used in various applications, such as in design and architecture, where precise measurements of angles and distances are essential. In mathematics, secants are explored in the context of circle theorems, providing insights into the properties of lines and circles. In education, understanding secants helps students develop geometric reasoning and problem-solving skills, which are essential for advanced studies in geometry and trigonometry. |
Definition of a Circle |

|
Definition--Circle Concepts--Sector | SectorTopicCircles DefinitionA sector is a portion of a circle enclosed by two radii and the arc between them. DescriptionSectors are fundamental in the study of circles, representing a portion of the circle's area. These shapes are used in various applications, such as in design and architecture, where precise measurements of angles and areas are essential. The area of a sector is calculated using the formula A = 1/2r2θ |
Definition of a Circle |
|
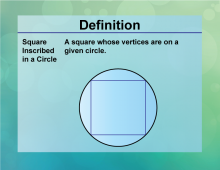
Definition--Circle Concepts--Square Inscribed in a Circle | Square Inscribed in a CircleTopicCircles DefinitionA square inscribed in a circle has its vertices touching the circle. |
Definition of a Circle |
|
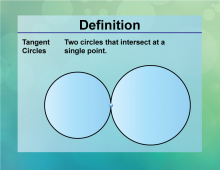
Definition--Circle Concepts--Tangent Circles | Tangent CirclesTopicCircles DefinitionTangent circles are two or more circles that intersect at exactly one point. |
Definition of a Circle |
|
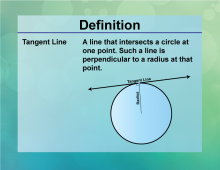
Definition--Circle Concepts--Tangent Line | Tangent LineTopicCircles DefinitionA tangent line is a straight line that touches a circle at exactly one point. |
Definition of a Circle |
|
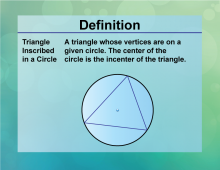
Definition--Circle Concepts--Triangle Inscribed in a Circle | Triangle Inscribed in a CircleTopicCircles DefinitionA triangle inscribed in a circle has its vertices on the circle. |
Definition of a Circle |
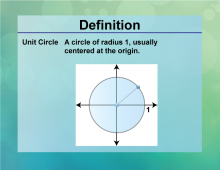
|
Definition--Circle Concepts--Unit Circle | Unit CircleTopicCircles DefinitionThe unit circle is a circle with a radius of one, centered at the origin of the coordinate plane. |
Definition of a Circle |

|
Formulas--Surface Area of a Cube | Formulas--Surface Area of a Cube
The formula for the Surface Area of a Cube. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
Formulas--Surface Area of a Cylinder | Formulas--Surface Area of a Cylinder
The formula for the Surface Area of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area and Cylinders |
|
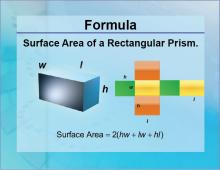
Formulas--Surface Area of a Rectangular Prism | Formulas--Surface Area of a Rectangular Prism
The formula for the Surface Area of a Rectangular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
Formulas--Surface Area of a Sphere | Formulas--Surface Area of a Sphere
The formula for the Surface Area of a Sphere. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
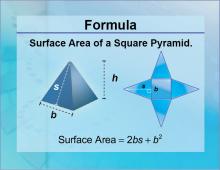
Formulas--Surface Area of a Square Pyramid | Formulas--Surface Area of a Square Pyramid
The formula for the Surface Area of a Square Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
|
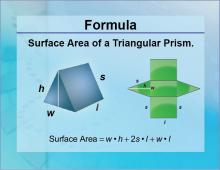
Formulas--Surface Area of a Triangular Prism | Formulas--Surface Area of a Triangular Prism
The formula for the Surface Area of a Triangular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
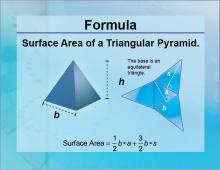
|
Formulas--Surface Area of a Triangular Pyramid | Formulas--Surface Area of a Triangular Pyramid
The formula for the Surface Area of a Triangular Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
Formulas--Volume of a Cube | Formulas--Volume of a Cube
The formula for the Volume of a Cube. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Cylinder | Formulas--Volume of a Cylinder
The formula for the Volume of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume and Cylinders |
|
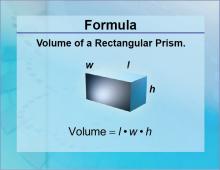
Formulas--Volume of a Rectangular Prism | Formulas--Volume of a Rectangular Prism
The formula for the Volume of a Recantular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Sphere | Formulas--Volume of a Sphere
The formula for the Volume of a Sphere. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |
|
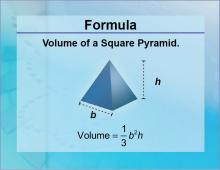
Formulas--Volume of a Square Pyramid | Formulas--Volume of a Square Pyramid
The formula for the Volume of a Square Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |
|
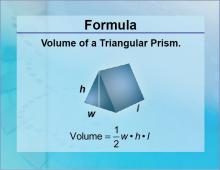
Formulas--Volume of a Triangular Prism | Note: The download is a JPG file. Related ResourcesTo see the complete collection of Formulas, click on this link: https://media4math.com/math-formulas |
Volume |
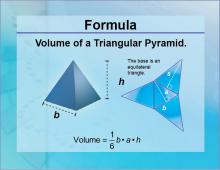
|
Formulas--Volume of a Triangular Pyramid | Volume of a Triangular Pyramid
Watch this video to learn about the volume of a pyramid. (The video transcript is also included.) Your browser does not support the video tag. Video Transcript Pyramids are majestic and a bit mysterious. Arising from deserts and jungles, they are grand in size and sleek in appearance. Mathematically, pyramids also have an air of mystery. Let’s take a closer look. Here is a cube of side s. Its volume couldn’t be more straightforward: s • s •s, or s-cubed. Its name, its shape, its volume are straightforward. |
Volume |

|
Geometry Applications Teachers Guide: 3D Geometry | Geometry Applications Teachers Guide: 3D Geometry
This is the Teacher's Guide that accompanies Geometry Applications: 3D Geometry. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of 3D Geometry |

|
Google Earth Voyager Story: Circular Structures, Part 2 | Google Earth Voyager Story: Circular Structures, Part 2TopicGeometric Models |
Applications of Circles and Cylinders |
|
Instructional Resource--Geometric Construction--Constructing an Egg Shape | Instructional Resource | Geometric Construction | An Egg Shape
In this instructional resource, we show the steps in constructing an egg shape. In the process, students learn about using common points of tangency to create smooth curves from two different shapes. This activity can be done with pencil, compass, ruler, and grid paper. —PRESS PREVIEW TO VIEW THE ACTIVITY— To see the complete collection of Instructional Resource, click on this link. |
Geometric Constructions with Circles |

|
INSTRUCTIONAL RESOURCE: Math Examples 1 | INSTRUCTIONAL RESOURCE: Math Examples--Circular Area and Circumference
This set of tutorials provides 23 examples of solving for the area and circumferences of circles and sections of circles. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Area and Circumference |

|
INSTRUCTIONAL RESOURCE: Math Examples 55 | INSTRUCTIONAL RESOURCE: Math Examples--Surface Area
This set of tutorials provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Surface Area |
|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Lesson Plan: Cross-Sections of 3D Figures, Part 1 | Lesson Plan: Cross-Sections of 3D Figures In this engaging math lesson, students explore cross-sections of cubes, cylinders, and cones through interactive activities, real-world examples, and animated visuals. They will learn how slicing three-dimensional shapes in different ways produces a variety of two-dimensional figures, helping to develop spatial reasoning and geometric understanding. The lesson begins with a conceptual introduction to cross-sections, followed by hands-on practice with everyday objects such as gift boxes, paper towel rolls, and ice cream cones. Students will investigate how horizontal, vertical, and diagonal slices impact the resulting shapes. Animated GIFs illustrate these concepts, reinforcing learning through dynamic visual representations. |
3-Dimensional Figures |

|
Math Clip Art--3D Figures--Cylinder | Math Clip Art--3D Figures--Cylinder
This collection of clip art images includes images of 3D figures and composite figures. |
3-Dimensional Figures and Applications of 3D Geometry |
|
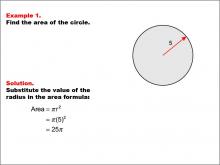
Math Example--Area and Perimeter--Circular Area and Circumference: Example 1 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 1TopicGeometry DescriptionThis example presents a circle with a radius of 5 units. The task is to calculate the area of the circle using the given radius. The solution involves substituting the radius value into the area formula: A = π * r^2 = π * (5)^2 = 25π. Understanding circular area and circumference is integral to mastering geometry. Concepts such as calculating areas and circumferences of circles are fundamental, and exercises like these examples not only provide practice but also deepen the understanding of theoretical concepts in a practical way. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 10TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 11TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π. |
Area and Circumference |
|
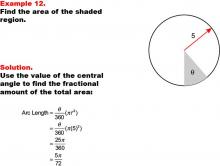
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 12TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 13TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π. |
Area and Circumference |
|
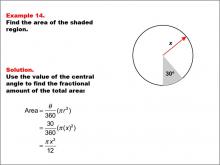
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 14TopicGeometry DescriptionThis example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 15 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 15TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the arc length of the shaded region in terms of x. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * (2 * π * x) = x / 6 * π. |
Area and Circumference |
|
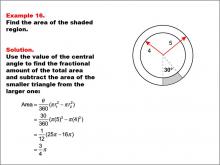
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 16TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4. |
Area and Circumference |