
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 13: The Volume of a Cylinder
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
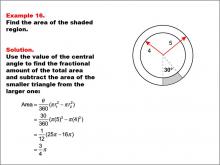
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 16TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4. |
Area and Circumference |
|
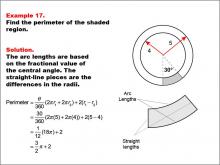
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 17TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 18 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 18TopicGeometry DescriptionThis example features two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x, y, and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * y2) = (θπ / 360) * (x2 - y2). |
Area and Circumference |
|
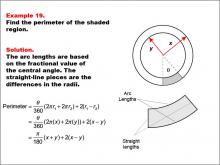
Math Example--Area and Perimeter--Circular Area and Circumference: Example 19 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 19TopicGeometry DescriptionThis example presents two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x, y, and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2πx + 2πy) + 2(x - y) = π/180 * θ(x + y) + 2(x - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 2 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 2TopicGeometry DescriptionThis example features a circle with a radius of 5 units. The objective is to calculate the circumference of the circle using the given radius. The solution involves applying the circumference formula: C = 2 * π * r = 2 * π * (5) = 10π. Circular area and circumference calculations are fundamental in geometry. These examples provide students with practical applications of theoretical concepts, helping them understand the relationship between a circle's radius and its circumference. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 20 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 20TopicGeometry DescriptionThis example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded region in terms of y. The solution involves calculating the difference between the areas of the larger and smaller circles, accounting for the central angle: Area = π/12 * (25 - y2). |
Area and Circumference |
|
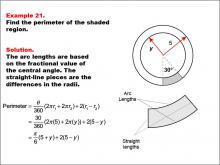
Math Example--Area and Perimeter--Circular Area and Circumference: Example 21 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 21TopicGeometry DescriptionThis example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. Given a central angle of 30 degrees, radius 5, and unknown radius y, the perimeter is calculated as: Perimeter = π/6 * (5 + y) + 2(5 - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 22 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 22TopicGeometry DescriptionThis example presents two concentric circles with radii 4 and x, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * 42) = (θ * π / 360) * (x2 - 16). |
Area and Circumference |
|
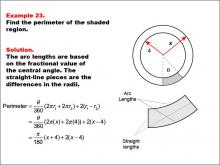
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 23TopicGeometry DescriptionThis example features two concentric circles with radii x and 4, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * x + 2 * π * 4) + 2 * (x - 4) = (π / 180) * θ(x + 4) + 2(x - 4). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 3 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 3TopicGeometry DescriptionThis example introduces a circle with an unknown radius represented by x. The task is to express the area of the circle in terms of x. The solution demonstrates how to use the area formula with a variable radius: A = π * r2 = π * (x)2 = π * x2. Working with variable expressions in geometry helps students transition from concrete to abstract thinking. This example bridges the gap between numerical calculations and algebraic representations, a crucial skill in advanced mathematics. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 4 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 4TopicGeometry DescriptionThis example presents a circle with an unknown radius represented by x. The task is to express the circumference of the circle in terms of x. The solution demonstrates how to use the circumference formula with a variable radius: C = 2 * π * r = 2 * π * x = 2πx. Understanding circular area and circumference is crucial in geometry. This example helps students transition from concrete numerical values to abstract algebraic expressions, fostering a deeper comprehension of the relationship between a circle's radius and its circumference. |
Area and Circumference |
|
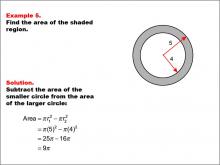
Math Example--Area and Perimeter--Circular Area and Circumference: Example 5 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 5TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units. The task is to calculate the area of the shaded region between these circles. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * (4)2 = 25π - 16π = 9π. Concentric circles and shaded regions introduce students to more complex geometric concepts. This example builds upon basic circular area calculations, encouraging students to think about the relationships between different circles and how to find areas of composite shapes. |
Area and Circumference |
|
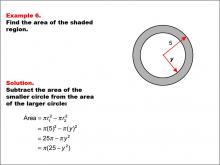
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 6TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2). |
Area and Circumference |
|
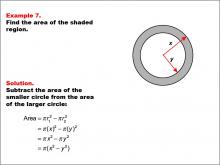
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 7TopicGeometry DescriptionThis example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2). |
Area and Circumference |
|
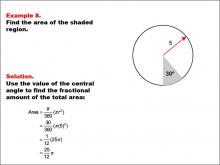
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 8TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 9TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6. |
Area and Circumference |
|
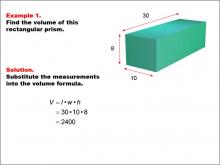
Math Example--Volume Concepts--Calculating Volume: Example 1 | Math Example--Volume Concepts--Calculating Volume: Example 1TopicVolume DescriptionA rectangular prism with dimensions labeled: length = 30, width = 10, and height = 8. The image shows how to find the volume of the prism using the formula for volume of a rectangular prism. This image illustrates Example 1: The caption explains how to calculate the volume of the rectangular prism using the formula V = l * w * h. The given dimensions are substituted into the formula: V = 30 * 10 * 8 = 2400.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
|
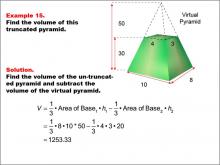
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
|
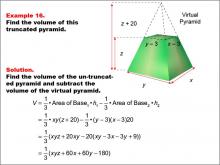
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 17 | Math Example--Volume Concepts--Calculating Volume: Example 17TopicVolume DescriptionA green sphere with a radius labeled as 3. The image is part of a math example showing how to calculate the volume of a sphere. This image illustrates Example 17: The text describes finding the volume of a sphere. The formula used is V = (4/3) * π * r3, where r = 3. After substituting, the result is V = 36π. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 18 | Math Example--Volume Concepts--Calculating Volume: Example 18TopicVolume Description
A green sphere with a radius labeled as x. This image is part of a math example showing how to calculate the volume of a sphere using an unknown radius. This image illustrates Example 18: The text explains how to find the volume of a sphere with an unknown radius x. The formula used is V = (4/3) * π * r3, and substituting r = x gives V = (4/3) * x3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 19 | Math Example--Volume Concepts--Calculating Volume: Example 19TopicVolume Description
A green cube with side length labeled as 7. The image illustrates how to calculate the volume of a cube with known side length. This image illustrates Example 19: The text describes finding the volume of a cube. The formula used is V = s3, where s = 7. After substituting, the result is V = 343. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |
|
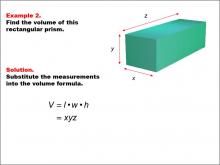
Math Example--Volume Concepts--Calculating Volume: Example 2 | Math Example--Volume Concepts--Calculating Volume: Example 2TopicVolume DescriptionA rectangular prism with dimensions labeled as x, y, and z. The image shows a general example of calculating the volume of a rectangular prism using variables instead of specific numbers. This image illustrates Example 2: The caption describes how to find the volume of a rectangular prism using variables for length (x), width (y), and height (z). The formula is given as V = x * y * z, but no specific values are provided. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 20 | Math Example--Volume Concepts--Calculating Volume: Example 20TopicVolume DescriptionA green cube with side length labeled as x. This image is part of a math example showing how to calculate the volume of a cube using an unknown side length. This image illustrates Example 20: The text explains how to find the volume of a cube with an unknown side length x. The formula used is V = s3, and substituting s = x gives V = x3. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 21 | Math Example--Volume Concepts--Calculating Volume: Example 21TopicVolume DescriptionA hollow cube with an outer edge of 9 and an inner hollow region with an edge of 7. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 21: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 is the outer edge (9) and s2 is the inner edge (7). The solution calculates 9^3 - 7^3 = 386.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 22 | Math Example--Volume Concepts--Calculating Volume: Example 22TopicVolume DescriptionA hollow cube with an outer edge of x and an inner hollow region with an edge of x - 2. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 22: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 = x and s2 = x - 2. Expanding and simplifying gives V = 6x2 - 12x + 8. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 23 | Math Example--Volume Concepts--Calculating Volume: Example 23TopicVolume Description
A cone with a height of 12 and a radius of 4. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 23: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = 4 and h = 12. Substituting these values gives V = (1/3) * π * (42) * 12 = 64π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 24 | Math Example--Volume Concepts--Calculating Volume: Example 24TopicVolume DescriptionA cone with a height labeled as y and a radius labeled as x. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 24: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = x and h = y. Substituting these variables gives V = (x^2 * y)/3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 3 | Math Example--Volume Concepts--Calculating Volume: Example 3TopicVolume DescriptionA hollow rectangular prism with outer dimensions: length = 60, width = 20, and height = 16. The inner hollow part has dimensions: length = 60, width = 18, and height = 14. The image shows how to subtract volumes to find the hollow volume. This image illustrates Example 3: The caption explains how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume. V = (60 * 20 * 16) - (60 * 18 * 14) = 4080. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 4 | Math Example--Volume Concepts--Calculating Volume: Example 4TopicVolume DescriptionA hollow rectangular prism with outer dimensions labeled as x, y, and z, and inner hollow dimensions labeled as x - 2 and y - 2. The image shows a symbolic calculation for finding the hollow volume using variables. This image illustrates Example 4: The caption describes how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume using variables: V = xyz - z(y - 2)(x - 2) = 2z(y + x - 2). |
Volume |
|
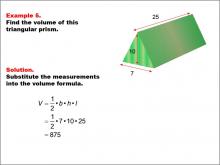
Math Example--Volume Concepts--Calculating Volume: Example 5 | Math Example--Volume Concepts--Calculating Volume: Example 5TopicVolume DescriptionThe image shows a triangular prism with dimensions labeled as base (7), height (10), and length (25). It is part of an example on how to calculate the volume of a solid triangular prism. This image illustrates Example 5: "Find the volume of this triangular prism." The solution involves substituting the given measurements into the volume formula for a triangular prism: V = 1/2 * b * h * l = 1/2 * 7 * 10 * 25 = 875. |
Volume |
|
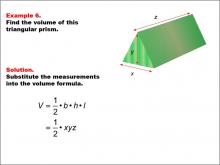
Math Example--Volume Concepts--Calculating Volume: Example 6 | Math Example--Volume Concepts--Calculating Volume: Example 6TopicVolume DescriptionThe image depicts a triangular prism with dimensions labeled as x, y, and z. The example demonstrates how to calculate the volume using a general formula for a triangular prism. This image illustrates Example 6: "Find the volume of this triangular prism." The solution uses the formula V = 1/2 * b * h * l, which is simplified to V = 1/2 * x * y * z.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 7 | Math Example--Volume Concepts--Calculating Volume: Example 7TopicVolume DescriptionThe image shows a hollow triangular prism with outer dimensions labeled as base (10), height (7), and length (35), and inner dimensions labeled as base (8) and height (5). The example calculates the volume by subtracting the hollow region from the full prism. This image illustrates Example 7: "Find the volume of this hollow triangular prism." The solution calculates the full volume using V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = 1/2 * 10 * 7 * 35 - 1/2 * 8 * 5 * 35 = 525.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 8 | Math Example--Volume Concepts--Calculating Volume: Example 8TopicVolume DescriptionThis image shows a hollow triangular prism with outer dimensions labeled as x, y, and z, and inner dimensions reduced by 2 units each. It demonstrates how to calculate the volume by subtracting the hollow region from the full prism. This image illustrates Example 8: "Find the volume of this hollow triangular prism." The solution uses V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = z(xy - (x - 2)(y - 2)) = z(x + y - 2).. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 9 | Math Example--Volume Concepts--Calculating Volume: Example 9TopicVolume Description
A green cylinder with a radius of 10 units and a height of 8 units. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 9: The task is to find the volume of the cylinder. The volume formula V = πr2h is used. Substituting the values r = 10 and h = 8, the volume is calculated as V= 800π. |
Volume |

|
Math Example--Volume Concepts--Modeling Volume--Example 1 | Math Example--Volume Concepts--Modeling Volume--Example 1TopicVolume DescriptionThe image shows a rectangular prism made up of 3 unit cubes arranged in a single row. The example asks for the volume of the figure, and the solution involves counting the number of unit cubes. Example 1: The figure consists of 3 unit cubes. The caption reads: "Count the number of unit cubes to find the volume. 3 unit cubes means that the volume is 3." |
Volume |

|
Math Example--Volume Concepts--Modeling Volume--Example 2 | Math Example--Volume Concepts--Modeling Volume--Example 2TopicVolume DescriptionThe image shows a figure made up of 4 unit cubes, with one cube stacked on top of another, forming an L-shape. The example asks for the volume, and the solution involves counting the cubes. Example 2: The figure consists of 4 unit cubes. The caption reads: "Count the number of unit cubes to find the volume. 4 unit cubes means that the volume is 4." |
Volume |
|
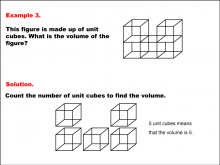
Math Example--Volume Concepts--Modeling Volume--Example 3 | Math Example--Volume Concepts--Modeling Volume--Example 3TopicVolume DescriptionThe image shows a figure made up of 5 unit cubes arranged in an irregular shape, with one cube raised above others. The example asks for the volume, and the solution involves counting the number of unit cubes. Example 3: The figure consists of 5 unit cubes. The caption reads: "Count the number of unit cubes to find the volume. 5 unit cubes means that the volume is 5." |
Volume |
|
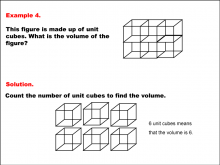
Math Example--Volume Concepts--Modeling Volume--Example 4 | Math Example--Volume Concepts--Modeling Volume--Example 4TopicFractions DescriptionThe image shows a rectangular prism made up of 6 unit cubes arranged in two layers (a top and bottom row). The example asks for the volume, and the solution involves counting all the cubes in both layers. Example 4: The figure consists of 6 unit cubes. The caption reads: "Count the number of unit cubes to find the volume. 6 unit cubes means that the volume is 6." |
Volume |
|
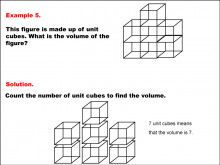
Math Example--Volume Concepts--Modeling Volume--Example 5 | Math Example--Volume Concepts--Modeling Volume--Example 5TopicFractions DescriptionThe image shows a 3D figure made up of unit cubes. The figure is stacked in a staggered manner, with some cubes placed directly on top of others. Below the figure, there is a breakdown showing the individual cubes counted to determine the volume. Example 5: The caption asks for the volume of the figure, which is made up of unit cubes. The solution involves counting the cubes to find the volume. |
Volume |

|
MATH EXAMPLES--Teacher's Guide: Circular Area and Circumference | MATH EXAMPLES--Teacher's Guide: Circular Area and Circumference
This set of tutorials provides 23 examples of solving for the area and circumferences of circles and sections of circles. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Area and Circumference |

|
MATH EXAMPLES--Teacher's Guide: Surface Area | MATH EXAMPLES--Teacher's Guide: Surface Area
This Teacher's Guide provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |

|
MATH EXAMPLES--Teacher's Guide: Volume | MATH EXAMPLES--Teacher's Guide: Volume
This set of tutorials provides 24 examples of how to find the volume of various 3-dimensional geometric figures. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
MATH EXAMPLES--Volume | MATH EXAMPLES--Volume
This set of tutorials provides 24 examples of how to find the volume of various 3-dimensional geometric figures. NOTE: The download is a PPT file. |
Volume |

|
Math in the News: Issue 13--Living Near Volcanoes | Math in the News: Issue 13--Living Near Volcanoes
6/13/11. In this issue we explore the volcanic eruption in Chile that resulted in a huge plume of smoke and ash that was miles high. We explore the viscosity of lava that makes such eruptions possible. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |