
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 19: Estimating a Hemisphere
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Clip Art--Linear Functions Concepts--Linear Function Representations 11 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 11TopicLinear Functions DescriptionThis image presents a function rule and its corresponding function equation for f(x) = 2x + 3. It demonstrates how a verbal description of a linear function can be translated into a mathematical equation, helping students bridge the gap between conceptual understanding and algebraic representation of linear functions. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Clip Art--Linear Functions Concepts--Linear Function Representations 12 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 12TopicLinear Functions DescriptionThis image presents a variation of the previous image, now showing the function f(x) = 3x + 4. It provides another example of how a function rule can be written as an equation, reinforcing the concept of translating verbal descriptions into mathematical expressions. |
Graphs of Linear Functions and Slope-Intercept Form |
|
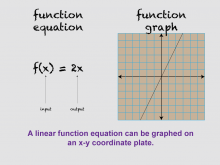
Math Clip Art--Linear Functions Concepts--Linear Function Representations 13 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 13TopicLinear Functions DescriptionThis image shows the equation and graph of f(x) = 2x, demonstrating how a linear function equation can be graphed on an x-y coordinate plane. It provides a visual representation of the relationship between the algebraic and geometric aspects of linear functions. By using this visual aid, teachers can help students understand how the components of a linear function equation relate to its graph. This image is particularly useful for discussing concepts such as slope, y-intercept, and the meaning of x and y in the context of a graph. |
Graphs of Linear Functions and Slope-Intercept Form |
|
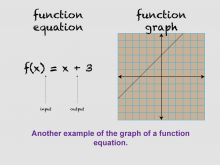
Math Clip Art--Linear Functions Concepts--Linear Function Representations 14 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 14TopicLinear Functions DescriptionThis image presents a variation of the previous image, now showing the equation and graph of f(x) = x + 3. It provides another example of how a function equation can be represented graphically, allowing students to compare and contrast different linear functions. By incorporating this visual aid, teachers can help students understand how changes in the equation affect the graph of a linear function. This image is particularly useful for discussing the effects of slope and y-intercept on the position and steepness of the line. |
Graphs of Linear Functions and Slope-Intercept Form |
|
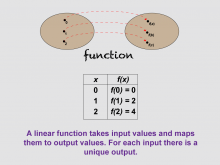
Math Clip Art--Linear Functions Concepts--Linear Function Representations 2 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 2TopicLinear Functions DescriptionThis image presents a function mapping and a table of values, illustrating how a linear function takes input values and maps them to unique output values. It helps students understand the fundamental concept of functions and their representation in tabular form. By incorporating this visual aid, teachers can enhance students' comprehension of the input-output relationship in linear functions. This image serves as a bridge between the abstract concept of functions and their concrete representation in tables. |
Graphs of Linear Functions and Slope-Intercept Form |
|
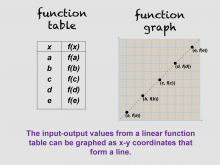
Math Clip Art--Linear Functions Concepts--Linear Function Representations 3 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 3TopicLinear Functions DescriptionThis image shows a function table alongside a linear graph, demonstrating how the input-output values from a linear function table can be graphed as x-y coordinates that form a line. It helps students visualize the connection between tabular and graphical representations of linear functions. By using this visual aid, teachers can help students understand how to translate data from a table into a graph. This image is particularly useful for students who benefit from seeing the direct relationship between different representations of the same function. |
Graphs of Linear Functions and Slope-Intercept Form |
|
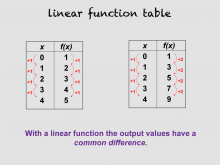
Math Clip Art--Linear Functions Concepts--Linear Function Representations 4 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 4TopicLinear Functions DescriptionThis image presents two data tables with common differences highlighted, illustrating that in a linear function, the output values have a common difference. This concept is crucial for understanding the constant rate of change in linear functions. By incorporating this visual aid, teachers can help students recognize patterns in linear functions and understand how these patterns relate to the function's behavior. This image is particularly useful for introducing the concept of slope in a tabular context. |
Graphs of Linear Functions and Slope-Intercept Form |
|
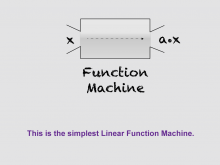
Math Clip Art--Linear Functions Concepts--Linear Function Representations 5 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 5TopicLinear Functions DescriptionThis image shows a simple function machine, introducing the concept of a Linear Function Machine. It provides a visual representation of how a function takes an input and produces an output, which is particularly helpful for students who benefit from concrete analogies. By using this visual aid, teachers can help students understand the basic concept of a function as a process that transforms inputs into outputs. This image serves as a foundation for more complex function machines and can help students grasp the idea of function composition. |
Graphs of Linear Functions and Slope-Intercept Form |
|
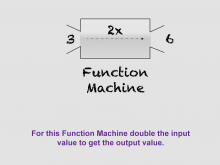
Math Clip Art--Linear Functions Concepts--Linear Function Representations 6 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 6TopicLinear Functions DescriptionThis image presents a function machine that outputs twice the value of the input, illustrating a specific example of a linear function. It helps students understand how a simple rule can be applied to transform input values into output values. By incorporating this visual aid, teachers can help students see the connection between the function machine concept and algebraic representations of linear functions. This image is particularly useful for introducing the idea of slope in a concrete, visual way. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Clip Art--Linear Functions Concepts--Linear Function Representations 7 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 7TopicLinear Functions DescriptionThis image shows the same function machine from the previous image, now with three different input-output examples. It demonstrates how a single function rule can be applied to various input values, reinforcing the concept of a function as a consistent transformation of inputs to outputs. By using this visual aid, teachers can help students understand how a single function rule applies across different input values. This image is particularly useful for helping students see patterns and predict outputs for given inputs. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Clip Art--Linear Functions Concepts--Linear Function Representations 8 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 8TopicLinear Functions DescriptionThis image presents a variation of the previous image, showing other Linear Function Machine examples. It helps students understand that there are many different types of linear functions, each with its own unique rule for transforming inputs into outputs. By incorporating this visual aid, teachers can expand students' understanding of the variety of linear functions. This image is particularly useful for demonstrating how different rules lead to different relationships between inputs and outputs. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Clip Art--Linear Functions Concepts--Linear Function Representations 9 | Math Clip Art--Linear Functions Concepts--Linear Function Representations 9TopicLinear Functions DescriptionThis image shows a function rule and its corresponding function equation for f(x) = 2x. It illustrates how a verbal description of a function rule can be translated into a mathematical equation, bridging the gap between conceptual understanding and algebraic representation. By using this visual aid, teachers can help students make the connection between the intuitive understanding of a function's behavior and its formal mathematical expression. This image is particularly useful for introducing the concept of variable notation and function notation. |
Graphs of Linear Functions and Slope-Intercept Form |
|
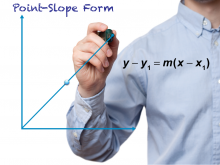
Math Clip Art--Linear Functions Concepts--Point-Slope Form 1 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 1TopicLinear Functions DescriptionThis image serves as a title card for a series of 9 clip art images that explore using the point-slope form to find a linear equation and graph. It sets the stage for understanding this important representation of linear functions, providing a visual introduction to the concept. Using visual aids like this title card can help engage students and prepare them for the upcoming content. It provides a clear introduction to the topic and helps organize the learning material in a visually appealing way. |
Graphs of Linear Functions and Slope-Intercept Form |
|
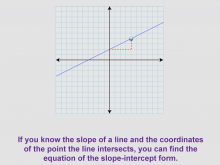
Math Clip Art--Linear Functions Concepts--Point-Slope Form 2 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 2TopicLinear Functions DescriptionThis image presents a linear graph with a stair step showing the rise over the run, illustrating the concept of slope. It introduces the idea that knowing the slope of a line and the coordinates of a point on the line allows us to find the equation in slope-intercept form. By incorporating this visual aid, teachers can help students understand the connection between the graphical representation of slope and its use in forming equations. This image is particularly useful for bridging the gap between visual and algebraic representations of linear functions. |
Graphs of Linear Functions and Slope-Intercept Form |
|
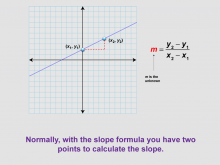
Math Clip Art--Linear Functions Concepts--Point-Slope Form 3 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 3TopicLinear Functions DescriptionThis image continues from the previous one, now labeling two coordinates on the graph and showing the general form of the slope formula. It emphasizes that typically, the slope formula is used when two points on the line are known. By using this visual aid, teachers can help students understand how the slope formula relates to points on a line. This image is particularly useful for reinforcing the concept of slope calculation before introducing the point-slope form. |
Graphs of Linear Functions and Slope-Intercept Form |
|
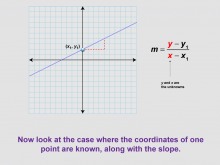
Math Clip Art--Linear Functions Concepts--Point-Slope Form 4 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 4TopicLinear Functions DescriptionThis image presents a variation of the previous graph, now with one coordinate highlighted. It introduces the case where the coordinates of one point are known, along with the slope of the line. This scenario sets the stage for introducing the point-slope form of a linear equation. By incorporating this visual aid, teachers can help students transition from the two-point slope formula to the point-slope form. This image is particularly useful for demonstrating how different pieces of information about a line can be used to determine its equation. |
Graphs of Linear Functions and Slope-Intercept Form |
|
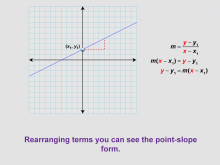
Math Clip Art--Linear Functions Concepts--Point-Slope Form 5 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 5TopicLinear Functions DescriptionThis image continues from the previous one, showing a rearrangement of the slope formula to derive the point-slope form. It demonstrates how algebraic manipulation can lead to a new, useful form of a linear equation. By using this visual aid, teachers can guide students through the process of deriving the point-slope form. This image is particularly useful for students who benefit from seeing the step-by-step transformation of mathematical expressions. |
Graphs of Linear Functions and Slope-Intercept Form |
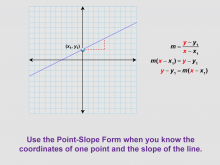
|
Math Clip Art--Linear Functions Concepts--Point-Slope Form 6 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 6TopicLinear Functions DescriptionThis image continues from the previous one, now showing the single coordinate values plugged into the point-slope equation. It demonstrates how to use the point-slope form when you know the coordinates of one point and the slope of the line. By incorporating this visual aid, teachers can help students understand how to apply the point-slope form in practice. This image is particularly useful for bridging the gap between the abstract form of the equation and its practical application. |
Graphs of Linear Functions and Slope-Intercept Form |
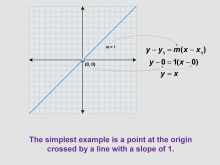
|
Math Clip Art--Linear Functions Concepts--Point-Slope Form 7 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 7TopicLinear Functions DescriptionThis image presents a graph crossing the origin and the corresponding point-slope form. It provides the simplest example of using the point-slope form, where a line passes through the origin (0,0) with a slope of 1. By using this visual aid, teachers can help students understand the point-slope form in its most basic application. This image is particularly useful for building confidence before moving on to more complex examples. |
Graphs of Linear Functions and Slope-Intercept Form |
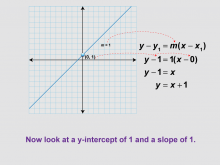
|
Math Clip Art--Linear Functions Concepts--Point-Slope Form 8 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 8TopicLinear Functions DescriptionThis image presents a variation of the previous example, now with the coordinate (0, 1) and a slope of 1. It demonstrates how to use the point-slope form when the y-intercept is not at the origin. By incorporating this visual aid, teachers can help students understand how the point-slope form can be used with different y-intercepts. This image is particularly useful for showing how the form adapts to different scenarios while maintaining its basic structure. |
Graphs of Linear Functions and Slope-Intercept Form |
|
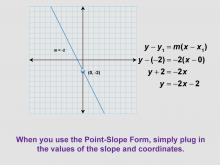
Math Clip Art--Linear Functions Concepts--Point-Slope Form 9 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 9TopicLinear Functions DescriptionThis image shows a variation of the previous example, now with a line having a negative slope of -2 and crossing the y-axis at (0, -2). It demonstrates how to use the point-slope form with negative slopes and y-intercepts. By using this visual aid, teachers can help students understand how the point-slope form accommodates negative values. This image is particularly useful for expanding students' understanding of the form's versatility. |
Graphs of Linear Functions and Slope-Intercept Form |
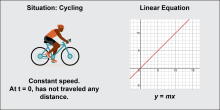
|
Math Clip Art: Linear Function Models 1 | Math Clip Art--Linear Function Concepts--Linear Function Models 1TopicLinear Functions DescriptionThis math clip art image is part of a series illustrating key linear function concepts. It depicts a bicycle alongside a linear graph, demonstrating the concept of constant speed. The graph shows a linear function that crosses the origin and has a positive slope, representing a scenario where at the starting point (t = 0), no distance has been traveled. |
Applications of Linear Functions |
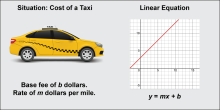
|
Math Clip Art: Linear Function Models 2 | Math Clip Art--Linear Function Concepts--Linear Function Models 2TopicLinear Functions DescriptionThis math clip art image is part of a series illustrating key linear function concepts. It features a taxi alongside a graph labeled "Situation: Cost of a Taxi". The graph represents a linear function with a positive y-intercept, demonstrating a scenario with a base fee and a rate per mile traveled. |
Applications of Linear Functions |
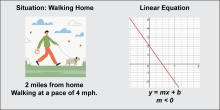
|
Math Clip Art: Linear Function Models 3 | Math Clip Art--Linear Function Concepts--Linear Function Models 3TopicLinear Functions DescriptionThis math clip art image is part of a series illustrating key linear function concepts. It depicts a person walking a dog alongside a graph labeled "Situation: Walking Home". The graph shows a linear function with a negative slope, representing a scenario where the distance from home decreases as time increases. |
Applications of Linear Functions |
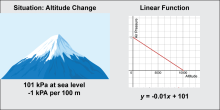
|
Math Clip Art: Linear Function Models 4 | Math Clip Art--Linear Function Concepts--Linear Function Models 4TopicLinear Functions DescriptionThis image is part of a series illustrating key concepts in linear functions, which are fundamental to understanding how lines behave in mathematics. The specific content of this image features a mountain and a graph titled "Situation: Altitude Change". It demonstrates a linear function with a negative slope, represented by the equation y = -0.01x + 101, showing how air pressure changes with altitude. |
Applications of Linear Functions |
|
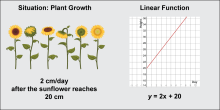
Math Clip Art: Linear Function Models 5 | Math Clip Art--Linear Function Concepts--Linear Function Models 5TopicLinear Functions DescriptionThis image is part of a series illustrating key concepts in linear functions, which are essential for understanding how lines behave in mathematics. The specific content of this image features sunflowers and a graph titled "Situation: Plant Growth". It demonstrates a linear function with a positive slope, represented by the equation y = 2x + 20, showing how the height of a sunflower changes over time. |
Applications of Linear Functions |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 1 | Math Example--Linear Function Concepts--Linear Function Machines--Example 1TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 2x. This involves creating a table of values for x and f(x) using f(x) = 2x. The output for each x is calculated by multiplying x by 2. The results are f(x) = -4, -2, 0, 2, and 4 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 10 | Math Example--Linear Function Concepts--Linear Function Machines--Example 10TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x + 1. This involves creating a table of values for x and f(x) using f(x) = 3x + 1. The output for each x is calculated by tripling x and then adding 1. The results are f(x) = -5, -2, 1, 4, and 7 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 11 | Math Example--Linear Function Concepts--Linear Function Machines--Example 11TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 4 * x + 1. This involves a table created for x and f(x) values. By substituting each x value into f(x) = 4 * x + 1, the outputs are calculated as follows: -2 gives -7, -1 gives -3, 0 gives 1, 1 gives 5, and 2 gives 9. The common difference between successive outputs is +4, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 12 | Math Example--Linear Function Concepts--Linear Function Machines--Example 12TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 5 * x + 1. This involves a table created for x and f(x) values. substituting each x into f(x) = 5 * x + 1, the outputs are calculated: -2 gives -9, -1 gives -4, 0 gives 1, 1 gives 6, and 2 gives 11. the common difference between outputs is +5, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |
|
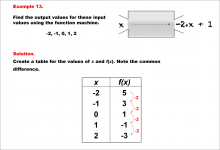
Math Example--Linear Function Concepts--Linear Function Machines--Example 13 | Math Example--Linear Function Concepts--Linear Function Machines--Example 13TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -2 * x + 1. This involves a table created for x and f(x) values. Substituting each x into f(x) = -2 * x + 1, the outputs are: -2 gives 5, -1 gives 3, 0 gives 1, 1 gives -1, and 2 gives -3. The common difference is -2, indicating a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |
|
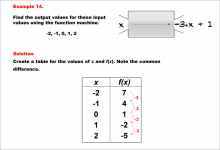
Math Example--Linear Function Concepts--Linear Function Machines--Example 14 | Math Example--Linear Function Concepts--Linear Function Machines--Example 14TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -3 * x + 1. This involves a table created for x and f(x) values. Each x substituted into f(x) = -3 * x + 1 yields: -2 gives 7, -1 gives 4, 0 gives 1, 1 gives -2, and 2 gives -5. The common difference is -3, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |
|
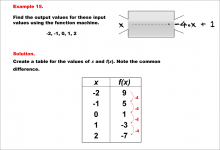
Math Example--Linear Function Concepts--Linear Function Machines--Example 15 | Math Example--Linear Function Concepts--Linear Function Machines--Example 15TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -4 * x + 1. This involves a table is created for x and f(x) values. Calculating for each x: -2 gives 9, -1 gives 5, 0 gives 1, 1 gives -3, and 2 gives -7. The common difference is -4, indicating linearity. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |
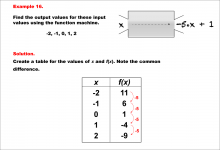
|
Math Example--Linear Function Concepts--Linear Function Machines--Example 16 | Math Example--Linear Function Concepts--Linear Function Machines--Example 16TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -5 * x + 1. This involves a table created for x and f(x) values. Substituting into f(x) = -5 * x + 1, the outputs are: -2 gives 11, -1 gives 6, 0 gives 1, 1 gives -4, and 2 gives -9. The common difference is -5, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 17 | Math Example--Linear Function Concepts--Linear Function Machines--Example 17TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 2. This involves a table created for x and f(x) values, where f(x) = 2 for all x values, resulting in outputs of 2, 2, 2, 2, and 2. The common difference is 0, indicating a constant function: y = 2. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 18 | Math Example--Linear Function Concepts--Linear Function Machines--Example 18TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 0. This involves a table created for x and f(x) values, where f(x) = 0 for all x values, giving outputs of 0, 0, 0, 0, and 0. The common difference is 0, indicating a constant function: y = 0. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 19 | Math Example--Linear Function Concepts--Linear Function Machines--Example 19TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = -1. This involves a table created for x and f(x) values, where f(x) = -1 for all x values, resulting in outputs of -1, -1, -1, -1, and -1. The common difference is 0, indicating a constant function: y = -1. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 2 | Math Example--Linear Function Concepts--Linear Function Machines--Example 2TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x. This involves creating a table of values for x and f(x) using f(x) = 3x. The output for each x is calculated by multiplying x by 3. the results are f(x) = -6, -3, 0, 3, and 6 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 3 | Math Example--Linear Function Concepts--Linear Function Machines--Example 3TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 4x. This involves creating a table of values for x and f(x) using f(x) = 4x. The output for each x is calculated by multiplying x by 4. The results are f(x) = -8, -4, 0, 4, and 8 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 4 | Math Example--Linear Function Concepts--Linear Function Machines--Example 4TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 5x. This involves creating a table of values for x and f(x) using f(x) = 5x. The output for each x is calculated by multiplying x by 5. The results are f(x) = -10, -5, 0, 5, and 10 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 5 | Math Example--Linear Function Concepts--Linear Function Machines--Example 5TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -2x. This involves creating a table of values for x and f(x) using f(x) = -2x. The output for each x is calculated by multiplying x by -2. The results are f(x) = 4, 2, 0, -2, and -4 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 6 | Math Example--Linear Function Concepts--Linear Function Machines--Example 6TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -3x. This involves creating a table of values for x and f(x) using f(x) = -3x. The output for each x is calculated by multiplying x by -3. The results are f(x) = 6, 3, 0, -3, and -6 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 7 | Math Example--Linear Function Concepts--Linear Function Machines--Example 7TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -4x. This involves creating a table of values for x and f(x) using f(x) = -4x. The output for each x is calculated by multiplying x by -4. The results are f(x) = 8, 4, 0, -4, and -8 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 8 | Math Example--Linear Function Concepts--Linear Function Machines--Example 8TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -5x. This involves creating a table of values for x and f(x) using f(x) = -5x. The output for each x is calculated by multiplying x by -5. The results are f(x) = 10, 5, 0, -5, and -10 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 9 | Math Example--Linear Function Concepts--Linear Function Machines--Example 9TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 2x + 1. This involves creating a table of values for x and f(x) using f(x) = 2x + 1. The output for each x is calculated by doubling x and then adding 1. The results are f(x) = -3, -1, 1, 3, and 5 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |
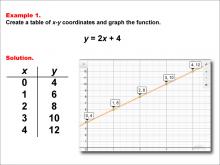
|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 1 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 1TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 2x + 4. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 4), (1, 6), (2, 8), (3, 10), and (4, 12), illustrating how the y-value increases by 2 for each unit increase in x. |
Graphs of Linear Functions |
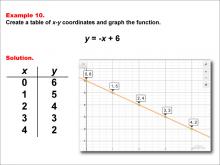
|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 10 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 10TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -x + 6. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 6), (1, 5), (2, 4), (3, 3), and (4, 2), illustrating how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
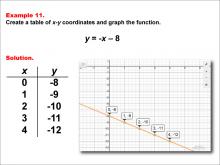
|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 11 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 11TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = -x - 8. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -8), (1, -9), (2, -10), (3, -11), and (4, -12), showing how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
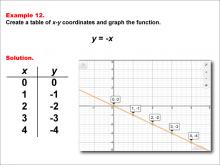
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 12 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 12TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = -x. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -1), (2, -2), (3, -3), and (4, -4), illustrating how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
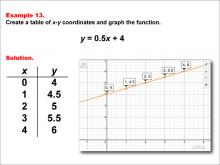
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 13 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 13TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0.5x + 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 4), (1, 4.5), (2, 5), (3, 5.5), and (4, 6), showing how the y-value increases by 0.5 for each unit increase in x. |
Graphs of Linear Functions |