
Illustrative Math Alignment: Grade 8 Unit 6
Associations in Data
Lesson 2: Plotting Data
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
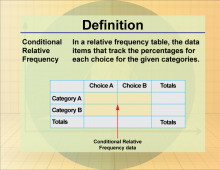
Definition--Statistics and Probability Concepts--Conditional Relative Frequency | Conditional Relative FrequencyTopicStatistics and Probability DefinitionConditional relative frequency is the ratio of the frequency of a subset of data to the frequency of a condition. DescriptionConditional relative frequency is crucial in analyzing categorical data, helping to understand the distribution of data under specific conditions. For example, the frequency of students who pass a test given they have attended all classes is a conditional relative frequency. Understanding this concept helps students interpret data in surveys and experiments more accurately. |
Data Analysis |
|
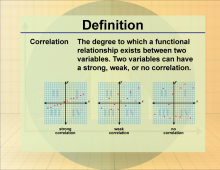
Definition--Statistics and Probability Concepts--Correlation 1 | Correlation 1TopicStatistics and Probability DefinitionCorrelation measures the strength and direction of a linear relationship between two variables. DescriptionCorrelation is widely used in statistics to assess the relationship between variables, such as height and weight, and is applicable in fields like economics, psychology, and biology. A positive correlation indicates that as one variable increases, the other also increases. Understanding correlation helps students make predictions and understand data trends. |
Data Analysis |
|
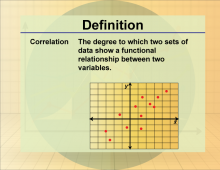
Definition--Statistics and Probability Concepts--Correlation 2 | Correlation 2TopicStatistics and Probability DefinitionCorrelation measures the strength and direction of a linear relationship between two variables. DescriptionCorrelation is widely used in statistics to assess the relationship between variables, such as height and weight, and is applicable in fields like economics, psychology, and biology. A positive correlation indicates that as one variable increases, the other also increases. Understanding correlation helps students make predictions and understand data trends. |
Data Analysis |
|
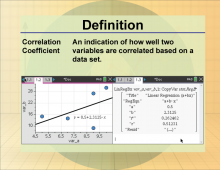
Definition--Statistics and Probability Concepts--Correlation Coefficient | Correlation CoefficientTopicStatistics and Probability DefinitionThe correlation coefficient is a measure that quantifies the degree to which two variables are related. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Dependent Event | Dependent EventTopicStatistics and Probability DefinitionA dependent event is an event whose outcome is influenced by the outcome of a preceding event. |
Probability |
|
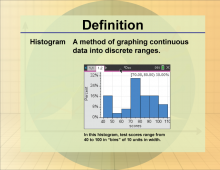
Definition--Statistics and Probability Concepts--Histogram | HistogramTopicStatistics and Probability DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are a fundamental tool in statistics for visualizing the frequency distribution of a dataset. They are used across various fields, including economics, biology, and engineering, to analyze data patterns and trends. By displaying data in intervals, histograms help identify the shape, central tendency, and variability of data. For students, understanding histograms is crucial for interpreting data visually and making informed decisions based on statistical evidence. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Independent Event | Independent EventTopicStatistics and Probability DefinitionAn independent event is an event whose outcome is not affected by the outcome of another event. DescriptionIndependent events are a key concept in probability, where the occurrence of one event does not influence another. This principle is applied in various fields, such as quality control, where the failure of one product does not affect others. Understanding independent events is essential for students to accurately calculate probabilities and analyze situations where events occur without influencing each other. |
Probability |
|
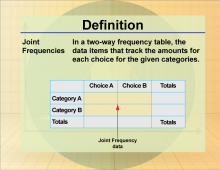
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |
|
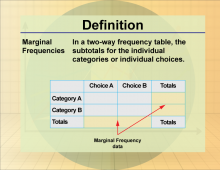
Definition--Statistics and Probability Concepts--Marginal Frequencies | Marginal FrequenciesTopicStatistics and Probability DefinitionMarginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. DescriptionMarginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability | Multiplication Rule of ProbabilityTopicStatistics and Probability DefinitionThe multiplication rule of probability is used to find the probability of two independent events both occurring. DescriptionThe multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory. |
Data Analysis |
|
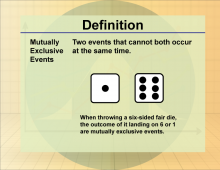
Definition--Statistics and Probability Concepts--Mutually Exclusive Events | Mutually Exclusive EventsTopicStatistics and Probability DefinitionMutually exclusive events are events that cannot occur simultaneously. DescriptionIn probability, mutually exclusive events are crucial for understanding scenarios where the occurrence of one event precludes the occurrence of another. This concept is applied in decision-making processes, such as project management, where choosing one option excludes others. For students, grasping mutually exclusive events is important for accurately calculating probabilities and understanding the structure of probability spaces. |
Probability |

|
Definition--Statistics and Probability Concepts--Permutation 1 | Permutation 1TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Permutation 2 | Permutation 2TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is
|
Probability |

|
Definition--Statistics and Probability Concepts--Population | PopulationTopicStatistics and Probability DefinitionA population is the entire group under consideration in a statistical study. DescriptionPopulation is a fundamental concept in statistics, representing the complete set of individuals or items that share a common characteristic. Understanding a population is crucial for statistical analysis as it serves as the basis for sampling and inferential statistics. |
Data Gathering |
|
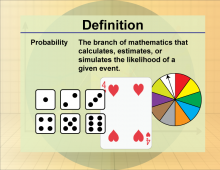
Definition--Statistics and Probability Concepts--Probability | ProbabilityTopicStatistics and Probability DefinitionProbability quantifies the likelihood of an event occurring. DescriptionProbability is a key concept in statistics that assesses the chance that a specific event will occur out of all possible outcomes. This concept is widely used in various fields such as gambling, insurance, and any scenario involving uncertainty. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability Model | Probability ModelTopicStatistics and Probability DefinitionA probability model is a mathematical representation of a random phenomenon. DescriptionProbability models are essential in understanding how to quantify uncertainty in various scenarios. They can be as simple as a coin toss or as complex as predicting stock market trends. These models usually incorporate the outcomes of an event and their associated probabilities. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability Notation | Probability NotationTopicStatistics and Probability DefinitionProbability notation is a standardized way of expressing probabilities. DescriptionProbability notation provides a concise language for defining and communicating probabilities in mathematics. It helps in avoiding confusion in statistical communication. Common symbols include P(A) for the probability of event A occurring. |
Data Analysis |
|
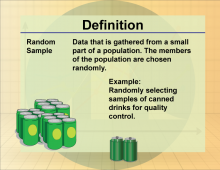
Definition--Statistics and Probability Concepts--Random Sample | Random SampleTopicStatistics and Probability DefinitionA random sample is a subset of individuals chosen from a larger population, selected in such a way that every individual has an equal chance of being chosen. DescriptionRandom sampling is a critical technique in statistics that helps ensure the representativeness of a sample by minimizing bias. It is widely used in survey research to ensure that the data collected reflects the diversity and characteristics of the entire population. |
Data Gathering |

|
Definition--Statistics and Probability Concepts--Relative Frequency Table | Relative Frequency TableTopicStatistics and Probability DefinitionA relative frequency table displays the proportion of total occurrences for each category of data. DescriptionRelative frequency tables are important in statistics as they summarize data in a way that makes it easy to analyze proportions and patterns within datasets. These tables allow for quick comparisons of different categories based on their frequency relative to the total. |
Data Analysis |
|
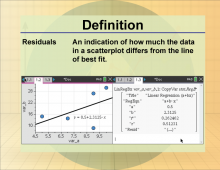
Definition--Statistics and Probability Concepts--Residuals | ResidualsTopicStatistics and Probability DefinitionResiduals are the differences between observed and predicted values in a dataset. DescriptionIn statistics, residuals are crucial for assessing the accuracy of predictions generated by statistical models. They represent the errors in prediction, providing insight into the model's performance and areas for potential improvement. |
Data Analysis |
|
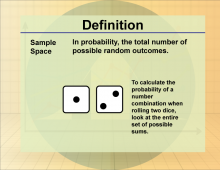
Definition--Statistics and Probability Concepts--Sample Space | Sample SpaceTopicStatistics and Probability DefinitionA sample space is the set of all possible outcomes in a probability experiment. DescriptionThe sample space is a foundational concept in probability, providing the framework within which probabilities are assigned to events. It is used in various fields, such as finance, to model different investment outcomes, or in engineering to predict system failures. Understanding the sample space is crucial for students to accurately calculate probabilities and analyze different scenarios. It helps them develop a comprehensive understanding of how different events relate to each other within a probability model. |
Probability |
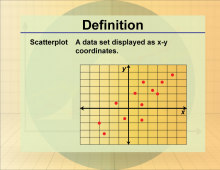
|
Definition--Statistics and Probability Concepts--Scatterplot | ScatterplotTopicStatistics and Probability DefinitionA scatterplot is a graphical representation of the relationship between two numerical variables. DescriptionScatterplots are essential tools in statistics for visualizing the correlation between two variables. They are widely used in fields like economics and biology to identify trends and relationships in data. For students, understanding scatterplots is important for interpreting data visually and analyzing the strength and direction of relationships between variables. This skill is crucial for developing their ability to conduct statistical analyses and draw meaningful conclusions from data. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Statistic | StatisticTopicStatistics and Probability DefinitionA statistic is a numerical measure that describes a characteristic of a sample. DescriptionStatistics are vital in summarizing and analyzing data, providing insights into trends and patterns. They are used in various fields, including healthcare, to determine the effectiveness of treatments, or in business to assess consumer preferences. Understanding statistics is essential for students to interpret data accurately and make informed decisions based on statistical evidence. This knowledge forms the basis for more advanced statistical studies and applications. |
Data Gathering |

|
Definition--Statistics and Probability Concepts--Statistical Distribution | Statistical DistributionTopicStatistics and Probability DefinitionA statistical distribution describes how values of a variable are distributed. DescriptionStatistical distributions are fundamental in understanding data behavior and variability. They are used in various fields, such as finance, to model asset returns, or in biology, to understand population dynamics. Common distributions include normal, binomial, and Poisson distributions, each with its own properties and applications. |
Data Gathering |

|
Definition--Statistics and Probability Concepts--Statistical Variability | Statistical VariabilityTopicStatistics and Probability DefinitionStatistical variability refers to the extent to which data points in a dataset differ from each other and from the central value. DescriptionUnderstanding variability is essential in statistics as it provides insights into the consistency and reliability of data. Measures of variability, such as range, variance, and standard deviation, help in assessing the spread of data points around a central value. |
Data Gathering |

|
Definition--Statistics and Probability Concepts--Stem-and-Leaf Plot | Stem-and-Leaf PlotTopicStatistics and Probability DefinitionA stem-and-leaf plot is a graphical representation that organizes data points based on their place value. DescriptionStem-and-leaf plots are useful for displaying the distribution of a dataset in a concise format, preserving the original data while showing its shape. They are particularly helpful in exploratory data analysis to identify patterns and outliers. In educational settings, stem-and-leaf plots are used to teach students about data organization and visualization. Understanding this concept helps students develop skills in data interpretation and enhances their ability to summarize data effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Two-Way Frequency Table | Two-Way Frequency TableTopicStatistics and Probability DefinitionA two-way frequency table displays the frequency of data points across two categorical variables. DescriptionTwo-way frequency tables are essential for analyzing the relationship between two categorical variables, often used in survey analysis to explore associations between different demographic factors. They help in identifying patterns and correlations within datasets. |
Data Analysis |

|
Formulas--Median | Formulas--Median
The formula for the Median. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Formulas--Sum of Consecutive Integers | Formulas--Sum of Consecutive Integers
The formula for the Sum of Consecutive Integers. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Sequences and Series |

|
Formulas--Sum of Consecutive Odd Integers | Formulas--Sum of Consecutive Odd Integers
The formula for the Sum of Consecutive Integers. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Sequences and Series |

|
HTML5 Interactive: Data Displays | HTML5 Interactive: Data Displays
In this interactive, review seven commonly used data displays. Provides a quck review tool for a unit on data analysis. Note: the download is the Teacher's Guide. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Data Gathering and Data Analysis |

|
Instructional Resource--Fibonacci Sequence, Lesson 1 | Instructional Resource | Fibonacci Sequence, Lesson 1
The year 2023 is the Year of the Rabbit in the Chinese Zodiac. Media4Math would also like to make this the Year of Fibonacci. If you recall, Fibonacci investigated his famous number pattern by looking at the number pattern generated by the increase in the number of rabbits from month to month. The Fibonacci Sequence is one of the most important number patterns found in nature. —PRESS PREVIEW TO VIEW THE LESSON— To see the other lessons in this series, click on the link.Note: The download is a PDF file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Sequences |

|
Instructional Resource--Fibonacci Sequence, Lesson 2 | Instructional Resource | Fibonacci Sequence, Lesson 2
This is a continuation of our exploration of the Fibonacci Sequence. In this lesson we look at the sequence as an example of a recursive function. —PRESS PREVIEW TO VIEW THE LESSON— To see the other lessons in this series, click on the link.Note: The download is a PDF file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Sequences |
|
Instructional Resource--Segmented Bar Graphs | Instructional Resource | Constructing a Segmented Bar Graph
This tutorial goes over the construction of a segmented bar graph, along with how it differs from other chart types. —PRESS PREVIEW TO VIEW THE ACTIVITY— To see the complete collection of Instructional Resources, click on this link.Note: The download is a PDF file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Graphing a Scatterplot | In this Slide Show, learn how graph data in a scatterplot using the graph window. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Graphs of Linear Functions, Slope-Intercept Form and Data Analysis |

|
Interactive Math Game--Memory Game: Number Cubes | Interactive Math Game--Memory Game: Number Cubes
Use this math game to match different arrangements of dice. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
3-Dimensional Figures |

|
Interactive Word Search Puzzle--Data Analysis, Puzzle 1 | Interactive Word Search Puzzle--Data Analysis, Puzzle 1
Solve an interactive word search puzzle on the topic of Data Analysis. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Data Analysis |

|
Interactive Word Search Puzzle--Data Analysis, Puzzle 2 | Interactive Word Search Puzzle--Data Analysis, Puzzle 2
Solve an interactive word search puzzle on the topic of Data Analysis. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Data Analysis |

|
Interactive Word Search Puzzle--Data Analysis, Puzzle 3 | Interactive Word Search Puzzle--Data Analysis, Puzzle 3
Solve an interactive word search puzzle on the topic of Data Analysis. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Data Analysis |

|
Interactive Word Search Puzzle--Data Analysis, Puzzle 4 | Interactive Word Search Puzzle--Data Analysis, Puzzle 4
Solve an interactive word search puzzle on the topic of Data Analysis. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Data Analysis |

|
Interactive Word Search Puzzle--Data Analysis, Puzzle 5 | Interactive Word Search Puzzle--Data Analysis, Puzzle 5
Solve an interactive word search puzzle on the topic of Data Analysis. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 1 | Math Example--Measures of Central Tendency--Mean: Example 1TopicMeasures of Central Tendency DescriptionThis example demonstrates how to calculate the mean of a dataset, a fundamental concept in statistics. The mean, often referred to as the average, is a measure of central tendency that provides insight into the typical value of a dataset. By visually presenting the calculation process, students can better grasp the concept and its application in real-world scenarios. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 10 | Math Example--Measures of Central Tendency--Mean: Example 10TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the numbers 16, 18, 0, 19, 12, 10, 7, and 20. The process involves summing all values (102) and dividing by the count of numbers (8), resulting in a mean of 12.75. This example highlights how the mean can provide a representative value for a dataset that includes both high and low numbers, including zero. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 11 | Math Example--Measures of Central Tendency--Mean: Example 11TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the numbers 9, 3, 19, 9, 15, 15, 20, 7, and 2. The process involves summing all values (99) and dividing by the count of numbers (9), resulting in a mean of 11. This example demonstrates how the mean can provide a central value that represents a dataset with repeated numbers and a wide range of values. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 12 | Math Example--Measures of Central Tendency--Mean: Example 12TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the numbers 17, 3, 10, 12, 4, 17, 7, 17, and 19. The process involves summing all values (106) and dividing by the count of numbers (9), resulting in a mean of approximately 11.78. This example showcases how the mean can provide a representative value for a dataset that includes repeated numbers and a wide range of values. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 13 | Math Example--Measures of Central Tendency--Mean: Example 13TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the numbers 13, 7, 6, 19, 12, 7, 20, 9, 12, and 15. The process involves summing all values (120) and dividing by the count of numbers (10), resulting in a mean of 12. This example demonstrates how the mean can provide a central value that represents a dataset with repeated numbers and a wide range of values. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 14 | Math Example--Measures of Central Tendency--Mean: Example 14TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the numbers 10, 2, 7, 16, 16, 17, 3, 10, 18, and 15. The process involves summing all values (114) and dividing by the count of numbers (10), resulting in a mean of 11.4. This example showcases how the mean can provide a representative value for a dataset that includes repeated numbers and a wide range of values. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 15 | Math Example--Measures of Central Tendency--Mean: Example 15TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the numbers -11, 2, 5, and -16. The process involves summing all values (-20) and dividing by the count of numbers (4), resulting in a mean of -5. This example is particularly important as it demonstrates how to handle negative numbers when calculating the mean, a concept that often challenges students. |
Data Analysis |