
Illustrative Math Alignment: Grade 8 Unit 6
Associations in Data
Lesson 2: Plotting Data
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Measures of Central Tendency--Mode: Example 78 | Math Example--Measures of Central Tendency--Mode: Example 78TopicMeasures of Central Tendency DescriptionThe image depicts another math example on finding the mode. It includes a list of numbers that are sorted from least to greatest. The mode is identified and highlighted in red. This demonstrates how to identify multiple modes when two or more numbers appear with equal highest frequency in a data set. Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mode: Example 8 | Math Example--Measures of Central Tendency--Mode: Example 8TopicMeasures of Central Tendency DescriptionThis example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 8 includes a set of numbers with one mode highlighted. The numbers are sorted in ascending order, revealing that 8 appears twice, while all other numbers appear only once. This demonstrates how to identify the mode when one number occurs more frequently than others in a data set. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mode: Example 9 | Math Example--Measures of Central Tendency--Mode: Example 9TopicMeasures of Central Tendency DescriptionThis example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows an example of finding the mode from a set of numbers. The numbers are arranged from least to greatest, highlighting the most frequent ones. After sorting, it becomes clear that both 9 and 43 appear twice, while all other numbers appear only once. This example demonstrates that a data set can have more than one mode. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 1 | Math Example--Measures of Central Tendency--Range: Example 1TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 10 | Math Example--Measures of Central Tendency--Range: Example 10TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: -33, 38, 29, -8, 12, 2, 36, -8, 12, 18, -23, 50. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 83. This example is particularly useful as it includes both positive and negative numbers, helping students understand how to handle different types of values when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 11 | Math Example--Measures of Central Tendency--Range: Example 11TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 16, 50, 24, 31, 30, 6, 22, 32, 43, 27, 48, 17, 36. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 44. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 12 | Math Example--Measures of Central Tendency--Range: Example 12TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 34, 5, 43, 24, -48, -31, -49, 8, -41, 5, 0, 20, -41. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 92. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 13 | Math Example--Measures of Central Tendency--Range: Example 13TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 50, 18, 47, 29, 33, 27, 23, 34, 43, 17, 10, 15, 22. The solution involves arranging the numbers from least to greatest (10 to 50) and finding the difference between the two extremes. The range is calculated to be 40. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 14 | Math Example--Measures of Central Tendency--Range: Example 14TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 0, 12, -41, -47, 7, -29, -34, -24, 38, 25, 23, -9, 38, 12. The solution involves arranging the numbers from least to greatest (-47 to 38) and finding the difference between the two extremes. The range is calculated to be 85. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 15 | Math Example--Measures of Central Tendency--Range: Example 15TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 20, 13, 40, 45, 14, 2, 27, 16, 48, 43, 39, 44, 26, 12. The solution involves arranging the numbers from least to greatest (2 to 49) and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |
|
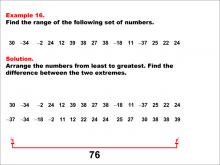
Math Example--Measures of Central Tendency--Range: Example 16 | Math Example--Measures of Central Tendency--Range: Example 16TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, -34, -2, 24, 12, 39, 38, 27, 38, -18, 11, -37, 25, 22, 24. The solution involves arranging the numbers from least to greatest (-37 to 39) and finding the difference between the two extremes. The range is calculated to be 76. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |
|
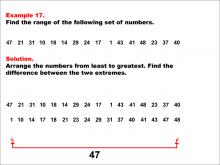
Math Example--Measures of Central Tendency--Range: Example 17 | Math Example--Measures of Central Tendency--Range: Example 17TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 47, 21, 31, 10, 18, 14, 29, 24, 17, 1, 43, 41, 48, 23, 37, 40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 18 | Math Example--Measures of Central Tendency--Range: Example 18TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: -2, -10, 24, -2, 26, 50, -40, 50, -40, 36, 30, -19, -40, 46, 27, -2. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 90. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 19 | Math Example--Measures of Central Tendency--Range: Example 19TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 14, 29, 44, 37, 9, 6, 41, 30, 19, 2, 38, 50, 26, 24, 40, 11, 45. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 2 | Math Example--Measures of Central Tendency--Range: Example 2TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 20 | Math Example--Measures of Central Tendency--Range: Example 20TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, 31, -27, 46, 25, 6, 41, 1, -27, 40, -8, -35, 9, -25, -25, -41, -38. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 87. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |
|
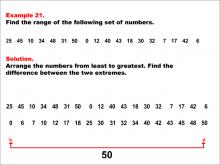
Math Example--Measures of Central Tendency--Range: Example 21 | Math Example--Measures of Central Tendency--Range: Example 21TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 25, 45, 10, 34, 48, 31, 50, 0, 12, 40, 43, 18, 30, 32, 7, 17, 42, 6. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 50. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
|
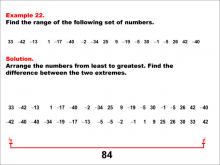
Math Example--Measures of Central Tendency--Range: Example 22 | Math Example--Measures of Central Tendency--Range: Example 22TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 33, -42, -13, 1, -17, -40, -2, -34, 25, 9, -19, -5, 30, -1, -5, 26, 42, -40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 84. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 23 | Math Example--Measures of Central Tendency--Range: Example 23TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
|
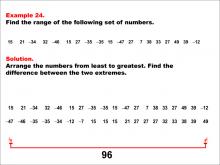
Math Example--Measures of Central Tendency--Range: Example 24 | Math Example--Measures of Central Tendency--Range: Example 24TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 15, 21, -34, 32, -46, 15, 27, -35, -35, 15, -47, 27, 7, 38, 33, 27, 49, 39, -12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 96. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 25 | Math Example--Measures of Central Tendency--Range: Example 25TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 42, 31, 16, 0, 35, 26, 30, 14, 6, 2, 13, 37, 33, 36, 19, 48, 3, 9, 45, 12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of non-negative numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 26 | Math Example--Measures of Central Tendency--Range: Example 26TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 28, 49, 1, -19, -37, 43, 27, 32, -10, 39, -19, -48, -49, 28, 36, 37, 44, 42, 29, -17. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 98. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 3 | Math Example--Measures of Central Tendency--Range: Example 3TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 4 | Math Example--Measures of Central Tendency--Range: Example 4TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 5 | Math Example--Measures of Central Tendency--Range: Example 5TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 6 | Math Example--Measures of Central Tendency--Range: Example 6TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 7 | Math Example--Measures of Central Tendency--Range: Example 7TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 8 | Math Example--Measures of Central Tendency--Range: Example 8TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 9 | Math Example--Measures of Central Tendency--Range: Example 9TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of a set of numbers: 22, 13, 15, 1, 16, 28, 3, 5, 18, 42, 8, 9. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 41. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a set of numbers and find their difference. The process encourages critical thinking and helps students visualize the relationship between numbers in a dataset. |
Data Analysis |

|
MATH EXAMPLES--The Mean | MATH EXAMPLES--The Mean
This set of tutorials provides 42 examples of calculating the mean. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Median | MATH EXAMPLES--The Median
This set of tutorials provides 40 examples of calculating the median. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Mode | MATH EXAMPLES--The Mode
This set of tutorials provides 78 examples of calculating the mode. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Range | MATH EXAMPLES--The Range
This set of tutorials provides 26 examples of calculating the range. NOTE: The download is a PPT file. |
Data Analysis |

|
Math in the News: Issue 103--Gas Prices | Math in the News: Issue 103--Gas Prices: Why Are They Decreasing?
December 2014. In this issue of Math in the News we analyze data in tabular and graphic formats to investigate the changing price of gasoline. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 104--The Decline of Radio Shack | Math in the News: Issue 104--The Decline of Radio Shack
December 2014. In this issue of Math in the News we analyze the reasons why Radio Shack has struggled as a business. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 105--Movie Statistics: 2014 | Math in the News: Issue 105--Movie Statistics: 2014
January 2015. In this issue of Math in the News we review box office statistics for the previous year. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 106--A Box Office Monster! | Math in the News: Issue 106--A Box Office Monster!
July 2015. In this issue of Math in the News we analyze the amazing box office success of the recently released Jurassic World. This provides an excellent application of data analysis and linear equations. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions, Standard Form and Data Analysis |

|
Math in the News: Issue 109--Was Ali the Greatest? | Math in the News: Issue 109--Was Ali the Greatest?
July 2016. In this issue of Math in the News we look at Muhammad Ali's boxing record and compare his record to other boxers. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 11--Taxing Tobacco | Math in the News: Issue 11--Taxing Tobacco
5/30/11. In this issue we look at the subject of taxation of tobacco products. Many states are using such taxes to meet budget shortfalls. What are the unintended consequences of these taxes? This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 110--Summer Travel | Math in the News: Issue 110--Summer Travel
August 2016. In this issue of Math in the News calculate average speed to various vacation destinations when traveling by car. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 111--Summer Blockbusters | Math in the News: Issue 111--Summer Blockbusters
August 2016. In this issue of Math in the News, look at real world box office data to analyze what makes a movie a blockbuster. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 113--Olympic Power | Math in the News: Issue 113--Olympic Power
November 2016. In this issue of Math in the News, we look at the history of the Olympics. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 114--Thanksgiving Dinner | Math in the News: Issue 114--Thanksgiving Dinner Grocery Shopping
November 2016. In this issue of Math in the News, we look at the history of Thanksgiving, as well as the cost of preparing the historically relevant meal. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 116: The 2021 Olympics | Math in the News: Issue 116: The 2021 Olympics
August 2021. In this issue of Math in the News we look at various charts and statistics about the Tokyo Olympics. Students are shown a series of charts and are then asked questions to encourage them to analyze the data. This is an excellent back-to-school activity with the focus on real-world data. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 117--Box Office Hits and Misses | Math in the News: Issue 117 | Box Office Hits and Misses
December 2022. In this issue of Math in the News we look at box office hits and misses from Disney. The House of Blockbosters every now and then misfires. It's useful to analyze box office data to see what we can learn from the hits and misses. —PRESS PREVIEW TO SEE THE SLIDE SHOW— This is part of the Math in the News collection. To see the complete collection, click on this link.Note: The download is a PPT file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 14--Will There Be an NFL Strike? | Math in the News: Issue 14--Will There Be an NFL Strike?
6/20/11. In this issue we look at the possibility of an NFL strike and what the issues are that keep players and owners from coming to agreement. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |
|
Math in the News: Issue 16--Blockbuster Math | Math in the News: Issue 16--Blockbuster Math
7/4/11. In this issue we look at box office receipts for blockbuster movies as well as flops. There is a characteristic curve that results for either type and we develop some regression models based on the data. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 17--Lone Star Employer | Math in the News: Issue 17--Lone Star Employer
7/11/11. In this issue we look at the underlying factors that make Texas such a powerhouse for employment. Using data from the Bureau of Labor Statistics and the Census Bureau, we dig into the numbers. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 19--Mr. 3000 | Math in the News: Issue 19--Mr. 3000
7/25/11. In this issue we look at the elite group of baseball players that have hit 3000 or more hits in their careers. The most recent is Derek Jeter, and based on the records of previous 3000+ hitters we explore whether he will make it to the Baseball Hall of Fame. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 47--The Rising Price of Gasoline | Math in the News: Issue 47--The Rising Price of Gasoline
February 2012. In this issue of Math in the News, we analyze data on the price of gasoline. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |