
Illustrative Math Alignment: Grade 8 Unit 9
Putting It All Together
Lesson 4: What Influences Temperature?
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
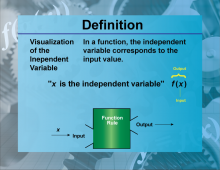
Definition--Functions and Relations Concepts--Visualization of the Independent Variable | Visualization of the Independent VariableTopicFunctions and Relations DefinitionVisualization of the independent variable involves graphically representing the variable that is manipulated to observe its effect on the dependent variable. |
Relations and Functions |
|
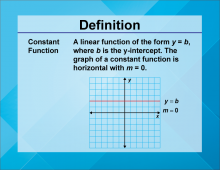
Definition--Linear Function Concepts--Constant Function | Constant Function
TopicLinear Functions DefinitionA constant function is a linear function of the form f(x) = b, where b is a constant. The graph of a constant function is a horizontal line. DescriptionConstant functions are a fundamental concept in linear functions. They represent scenarios where the output value remains unchanged, regardless of the input value. This is depicted graphically as a horizontal line, indicating that the function's rate of change is zero. In real-world applications, constant functions can model situations where a quantity remains steady over time. For example, a flat fee service charge that does not vary with usage can be represented as a constant function. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form | Converting from Standard Form to Slope-Intercept Form
TopicLinear Functions DefinitionConverting from standard form to slope-intercept form involves rewriting a linear equation from the form Ax + By = C to the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionConverting linear equations from standard form to slope-intercept form is a key skill in algebra. This conversion allows for easier graphing and interpretation of the equation's slope and y-intercept. |
Slope-Intercept Form |
|
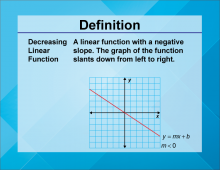
Definition--Linear Function Concepts--Decreasing Linear Function | Decreasing Linear Function
TopicLinear Functions DefinitionA decreasing linear function is a linear function where the slope is negative, indicating that as the input value increases, the output value decreases. DescriptionDecreasing linear functions are important in understanding how variables inversely relate to each other. The negative slope signifies a reduction in the dependent variable as the independent variable increases. Real-world examples include depreciation of assets over time or the decrease in temperature as altitude increases. These functions help model scenarios where an increase in one quantity results in a decrease in another. |
Slope-Intercept Form |
|
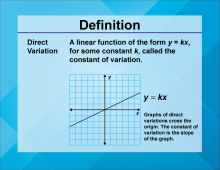
Definition--Linear Function Concepts--Direct Variation | Direct Variation
TopicLinear Functions DefinitionDirect variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. DescriptionDirect variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Equations of Parallel Lines | Equations of Parallel Lines
TopicLinear Functions DefinitionEquations of parallel lines are linear equations that have the same slope but different y-intercepts, indicating that the lines never intersect. DescriptionUnderstanding equations of parallel lines is crucial in geometry and algebra. Parallel lines have identical slopes, which means they run in the same direction and never meet. In real-world applications, parallel lines can model scenarios such as railway tracks or lanes on a highway, where maintaining a consistent distance is essential. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Equations of Perpendicular Lines | Equations of Perpendicular Lines
TopicLinear Functions DefinitionEquations of perpendicular lines are linear equations where the slopes are negative reciprocals of each other, indicating that the lines intersect at a right angle. DescriptionEquations of perpendicular lines are significant in both geometry and algebra. The negative reciprocal relationship between their slopes ensures that the lines intersect at a 90-degree angle. In real-world applications, perpendicular lines are found in various structures, such as the intersection of streets or the corners of a building, where right angles are essential. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Identity Function | Identity Function
TopicLinear Functions DefinitionAn identity function is a linear function of the form f(x) = x, where the output is equal to the input for all values of x. DescriptionThe identity function is a basic yet crucial concept in linear functions. It represents a scenario where the input value is always equal to the output value, graphically depicted as a 45-degree line passing through the origin. In real-world applications, the identity function can model situations where input and output are directly proportional and identical, such as converting units of the same measure. This also introduces the concept of identity, which is fundamental to mathematics. |
Slope-Intercept Form |
|
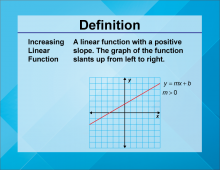
Definition--Linear Function Concepts--Increasing Linear Function | Increasing Linear Function
TopicLinear Functions DefinitionAn increasing linear function is a linear function where the slope is positive, indicating that as the input value increases, the output value also increases. DescriptionIncreasing linear functions are essential in understanding how variables positively relate to each other. The positive slope signifies an increase in the dependent variable as the independent variable increases. Real-world examples include income increasing with hours worked or the rise in temperature with the increase in daylight hours. These functions help model scenarios where an increase in one quantity results in an increase in another. |
Slope-Intercept Form |
|
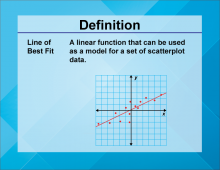
Definition--Linear Function Concepts--Line of Best Fit | Line of Best Fit
TopicLinear Functions DefinitionA line of best fit is a straight line that best represents the data on a scatter plot, showing the trend of the data points. DescriptionThe line of best fit is a crucial concept in statistics and data analysis. It helps in identifying the trend and making predictions based on the data. In real-world applications, the line of best fit is used in various fields such as economics, biology, and engineering to analyze trends and make forecasts. For example, it can be used to predict future sales based on past data. |
Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Linear Equations in Standard Form | Linear Equations in Standard Form
TopicLinear Functions DefinitionLinear equations in standard form are written as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. DescriptionLinear equations in standard form are a fundamental representation of linear functions. They provide a way to express linear relationships in a general form. |
Standard Form |
|
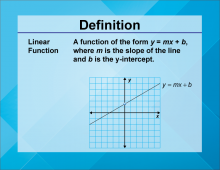
Definition--Linear Function Concepts--Linear Function | Linear Function
TopicLinear Functions DefinitionA linear function is a function that can be graphed as a straight line, typically written in the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionLinear functions are one of the most fundamental concepts in mathematics. They describe relationships where the rate of change between variables is constant, represented graphically as a straight line. This simplicity makes them a central topic in algebra and calculus. |
Slope-Intercept Form |
|
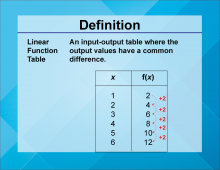
Definition--Linear Function Concepts--Linear Function Tables | Linear Function Tables
TopicLinear Functions DefinitionLinear function tables display the input-output pairs of a linear function, showing how the dependent variable changes with the independent variable. DescriptionLinear function tables are useful tools for understanding and analyzing linear relationships. They provide a clear way to see how changes in the input (independent variable) affect the output (dependent variable). |
Applications of Linear Functions and Graphs of Linear Functions |
|
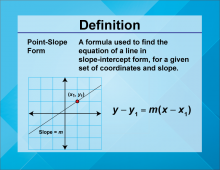
Definition--Linear Function Concepts--Point-Slope Form | Point-Slope Form
TopicLinear Functions DefinitionPoint-slope form of a linear equation is written as y − y1 = m(x−x1 ), where m is the slope and (x1 ,y1) is a point on the line. DescriptionThe point-slope form is a versatile way to express linear equations, especially useful when you know a point on the line and the slope. It allows for quick construction of the equation of a line. |
Point-Slope Form |
|
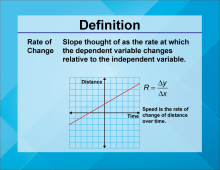
Definition--Linear Function Concepts--Rate of Change | Rate of Change
TopicLinear Functions DefinitionRate of change in a linear function is the ratio of the change in the dependent variable to the change in the independent variable, often represented as the slope m in the equation y = mx + b. DescriptionRate of change is a fundamental concept in understanding linear functions. It describes how one variable changes in relation to another, and is graphically represented by the slope of a line. |
Slope |

|
Definition--Linear Function Concepts--Slope-Intercept Form | Slope-Intercept Form
TopicLinear Functions DefinitionSlope-intercept form of a linear equation is written as y = mx + b, where m is the slope and b is the y-intercept. DescriptionSlope-intercept form is one of the most commonly used forms of linear equations. It provides a clear way to understand the slope and y-intercept of a line, making it easier to graph and interpret. In real-world applications, slope-intercept form is used in various fields such as economics, physics, and engineering to model linear relationships. For example, it can represent the relationship between cost and production levels in business. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--The Equation of a Line From Two Coordinates | The Equation of a Line From Two Coordinates
TopicLinear Functions DefinitionThe equation of a line from two coordinates can be determined by finding the slope between the two points and using it in the point-slope form of a linear equation. DescriptionFinding the equation of a line from two coordinates is a fundamental skill in algebra. It involves calculating the slope between the two points and then using one of the points to form the equation in point-slope or slope-intercept form. |
Point-Slope Form |
|
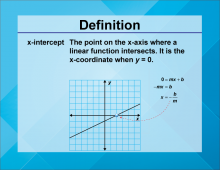
Definition--Linear Function Concepts--x-Intercept | x-Intercept
TopicLinear Functions DefinitionThe x-intercept is the point where a graph crosses the x-axis, indicating the value of x when 𝑦 y is zero. DescriptionThe x-intercept is a key concept in understanding the behavior of linear functions. It represents the point where the function's output is zero, providing insight into the function's roots and behavior. In real-world applications, the x-intercept can be used to determine break-even points in business, where revenue equals costs, or to find the time at which a process starts or stops. |
Slope-Intercept Form |
|
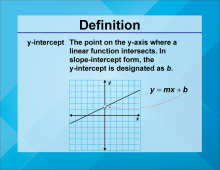
Definition--Linear Function Concepts--y-Intercept | y-Intercept
TopicLinear Functions DefinitionThe y-intercept is the point where a graph crosses the y-axis, indicating the value of y when x is zero. DescriptionThe y-intercept is a fundamental concept in understanding the behavior of linear functions. It represents the initial value of the function when the input is zero, providing insight into the function's starting point. In real-world applications, the y-intercept can be used to determine initial conditions in various scenarios, such as the starting balance in a bank account or the initial position of an object in motion. |
Slope-Intercept Form |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Creating an Exercise Chart | INSTRUCTIONAL RESOURCE: Algebra Application: Creating an Exercise Chart
In this Algebra Application, students develop a linear mathematical model based on the maximum heart rate during exercise based on age. Using this model, students investigate heart rate for moderate and vigorous workouts. The math topics covered include: Mathematical modeling, Linear functions, Families of functions, Computational thinking. The culminating activity is for students to create a simple program (using either a spreadsheet or a programming language like Python) to develop an exercise chart. This is a great back-to-school activity for middle school or high school students. A relevant real-world application allows them to review math concepts. |
Applications of Linear Functions and Slope-Intercept Form |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter | INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter
In this Algebra Application, students study the direction between diameter and circumference of a circle. Through measurement and data gathering students analyze the line of best fit and explore ways of calculating pi. The math topics covered include: Mathematical modeling, Linear functions, Data gathering and analysis, Ratios, Direct variation. This is a great back-to-school activity for middle school or high school students. This is also a great crossover activity that ties algebra and geometry. |
Applications of Linear Functions, Applications of Ratios, Proportions, and Percents and Applications of Circles |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Factored Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Factored Form
This slide show provides 8 examples of quadratic functions in factored form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Standard Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Standard Form
This slide show provides 18 examples of quadratic functions in standard form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Vertex Form | INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Vertex Form
This slide show provides 8 examples of quadratic functions in vertex form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions |

|
Instructional Resource: Applications of Linear Functions: Circumference vs. Diameter | In this Slide Show, apply concepts of linear functions to the context of circumference vs. diameter. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Cost vs. Time | In this Slide Show, apply concepts of linear functions to the context of cost vs. time data and graphs. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Cricket Chirps | In this Slide Show, apply concepts of linear functions to the context of cricket chirps. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Distance vs. Time | In this Slide Show, apply concepts of linear functions to the context of distance vs. time data and graphs. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Hooke's Law | In this Slide Show, apply concepts of linear functions to the context of Hooke's law. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions and Proportions |

|
Instructional Resource: Applications of Linear Functions: Momentum and Impulse | In this Slide Show, apply concepts of linear functions to the context of momentum and impulse. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Perimeter of a Rectangle | In this Slide Show, apply concepts of linear functions to the context of rectangular perimeter. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Saving Money | In this Slide Show, apply concepts of linear functions to the context of saving money. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Speed and acceleration | In this Slide Show, apply concepts of linear functions to the context of speed and acceleration. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
Instructional Resource: Applications of Linear Functions: Temperature Conversion | In this Slide Show, apply concepts of linear functions to the context of converting Celsius and Fahrenheit temperatures. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Desmos Tutorial: Matching Coordinates to Absolute Value Functions | INSTRUCTIONAL RESOURCE: Desmos Tutorial: Matching Coordinates to Absolute Value Functions
In this Slide Show, use the Desmos graphing calculator to explore absolute value functions. To see the complete collection of Desmos Resources click on this link. Note: The download is a PPT file. This is part of a collection of Desmos tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Special Functions |

|
INSTRUCTIONAL RESOURCE: Desmos Tutorial: Matching Coordinates to Linear Functions | INSTRUCTIONAL RESOURCE: Desmos Tutorial: Matching Coordinates to Linear Functions
In this Slide Show, use the Desmos graphing calculator to explore linear functions. To see the complete collection of Desmos Resources click on this link. Note: The download is a PPT file. This is part of a collection of Desmos tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Graphing Linear Functions | INSTRUCTIONAL RESOURCE: Tutorial: Graphing Linear Functions
In this Slide Show, learn about graphs of linear functions. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Tutorial: Linear Function Models | INSTRUCTIONAL RESOURCE: Tutorial: Linear Function Models
In this Slide Show, learn about linear function models. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Math Examples 12 | INSTRUCTIONAL RESOURCE: Math Examples--Equations of Parallel and Perpendicular Lines
The complete set of 32 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions and Graphs of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Math Examples 35 | INSTRUCTIONAL RESOURCE: Math Examples--Parallel and Perpendicular Lines
This set of tutorials provides 32examples that involve finding the equation of a line parallel or perpendicular to a given line and through a given point. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Linear Functions and Graphs of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Math Examples 58 | MATH EXAMPLES--Absolute Value Functions in Tabular and Graph Form
This set of tutorials provides 40 examples of absolute value functions in tabular and graph form. NOTE: The download is a PPT file. |
Special Functions |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Graphs of Absolute Value Functions | In this Slide Show, absolute value functions are graphed, including graphs centered at the origin, graphs displaced along the x-axis, and graphs displaced along the y-axis. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Special Functions |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Graphs of Inequalities | In this Slide Show, the Graph Window is used to graph linear inequalities. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Inequalities and Applications of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Graphs of Inequalities with Sliders | In this Slide Show, the Graph Window is used to graph inequalities using sliders. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Inequalities and Applications of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Graphs of Linear Functions | In this Slide Show, linear functions are graphed. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Applications of Linear Functions |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Parallel and Perpendicular Lines | In this Slide Show, explore the properties of parallel and perpendicular lines. Use a slider to define the slope and then graph parallel and perpendicular lines linked to this slider. |
Parallel Lines and Perpendicular Lines |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: The Perpendicular Bisectors of a Triangle | In this Slide Show, we show how to construct the perpendicular bisectors of the three sides of a triangle to show they intersect at a single point. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Definition of a Triangle and Geometric Constructions with Triangles |

|
Instructional Resource: TI-Nspire Activity: Exploring the Ratio of Circumference to Radius as a Linear Function | In this TI-Nspire Activity, use the Geometry and Graphing Tools to explore the ratio of Circumference to Radius as a linear function. Note: The Preview is a Google Slide Show and the download is a PPT. Subscribers to Media4Math can download resources. To see the complete collection of TI graphing calculator resources, click on this Link. |
Applications of Linear Functions, Applications of Circles and Geometric Constructions with Circles |