Digital Resources on the Topic of Polynomial Equations and Functions

On this page you'll find a sampling of the many resources on Media4Math that focus on the topic of Polynomial Functions. Media4Math is a digital library of over 15,000 resources on all key topics in K-12 math.

Subscribers can download these resources. Register and Subscribe today.

Number of Resources: 445

	Thumbnail Image	Description
Definition--Polynomial Concepts--Monomial		Monomial Topic Polynomials Definition A monomial is a polynomial with only one term.
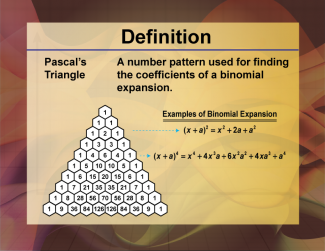
Definition--Polynomial Concepts--Pascal's Triangle		Pascal's Triangle Topic Polynomials
Definition--Polynomial Concepts--Polynomial		Polynomial Topic Polynomials
Definition--Polynomial Concepts--Polynomial Addition		Polynomial Addition Topic Polynomials
Definition--Polynomial Concepts--Polynomial Expansion		Polynomial Expansion Topic Polynomials
Definition--Polynomial Concepts--Polynomial Function		Polynomial Function Topic Polynomials
Definition--Polynomial Concepts--Polynomial Multiplication		Polynomial Multiplication Topic Polynomials
Definition--Polynomial Concepts--Polynomial Roots		Polynomial Roots Topic Polynomials
Definition--Polynomial Concepts--Polynomial Subtraction		Polynomial Subtraction Topic Polynomials
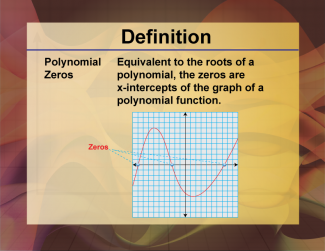
Definition--Polynomial Concepts--Polynomial Zeros		Polynomial Zeros Topic Polynomials
Definition--Polynomial Concepts--Rational Root Theorem		Rational Root Theorem Topic Polynomials
Definition--Polynomial Concepts--Remainder Theorem		Remainder Theorem Topic Polynomials
Definition--Polynomial Concepts--Sum of Cubes		Sum of Cubes Topic Polynomials
Definition--Polynomial Concepts--Synthetic Division		Synthetic Division Topic Polynomials
Definition--Polynomial Concepts--Trinomial		Trinomial Topic Polynomials Definition A trinomial is a polynomial with three terms.
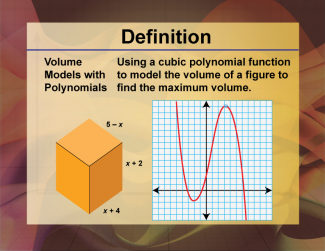
Definition--Polynomial Concepts--Volume Models with Polynomials		Volume Models with Polynomials Topic Polynomials
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx + c = 0		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx + c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 + bx + c = 0.
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx - c = 0		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx - c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 + bx - c = 0.
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx + c = 0		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx + c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 - bx + c = 0.
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx - c		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx - c In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 - bx - c = 0.
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^2 + bx + c = 0		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^2 + bx + c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: ax^2 + bx + c = 0.
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^2 + bx - c = 0		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^2 + bx - c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: ax^2 + bx - c = 0.
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^2 - bx + c = 0		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^2 - bx + c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: ax^2 - bx + c = 0.
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^2 - bx - c = 0		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^2 - bx - c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: ax^2 - bx - c = 0.
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^3 + bx^2 + cx + d = 0		INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax^3 + bx^2 + cx + d = 0 In this interactive, look at the solution to a polynomial equation of degree 3 using synthetic division. The equation is of the form ax^3 + bx^2 - cx - d = 0 and has three integer solutions.