
Illustrative Math Alignment: Grade 6 Unit 1
Reasoning to Find Area
Lesson 10: Bases and Heights of Triangles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
Animated Math Clip Art--Triangles--Acute Triangles 1 |
Animated Math Clip Art--Triangles--Acute Triangles 1TopicTriangles DescriptionThis animated clip art illustrates an acute triangle, where all angles are less than 90 degrees. Such visual aids are crucial for understanding the properties of triangles, particularly in identifying different types of triangles based on angles. By incorporating this image into lessons, students can visually distinguish acute triangles from other types, enhancing their comprehension through dynamic representation. |
Definition of a Triangle |
|
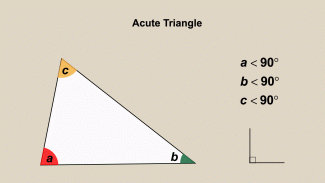
Animated Math Clip Art--Triangles--Acute Triangles 2 |
Animated Math Clip Art--Triangles--Acute Triangles 2TopicTriangles DescriptionThis animated clip art features another example of an acute triangle, reinforcing the concept that all angles are less than 90 degrees. Visualizing different acute triangles helps students grasp the range of shapes these triangles can take, promoting a better understanding of geometric diversity. Using animated math clip art in teaching not only clarifies concepts but also stimulates student interest. The animation provides a dynamic learning experience, making it easier for students to remember and apply their knowledge of triangles. Teachers can leverage this tool to create interactive lessons that encourage active participation. |
Definition of a Triangle |
|
Animated Math Clip Art--Triangles--Equilateral Triangles 1 |
Animated Math Clip Art--Triangles--Equilateral Triangles 1TopicTriangles DescriptionThis animation showcases an equilateral triangle, where all sides and angles are equal. This clip art is helpful in teaching the unique properties of equilateral triangles, helping students understand symmetry and equality in geometry. Animated math clip art is a powerful educational tool, particularly for visual learners. It brings static concepts to life, making them more accessible and memorable. Teachers can use this animation to explain symmetry and congruence, fostering a deeper appreciation for geometric principles. |
Definition of a Triangle |
|
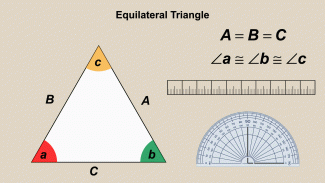
Animated Math Clip Art--Triangles--Equilateral Triangles 2 |
Animated Math Clip Art--Triangles--Equilateral Triangles 2TopicTriangles DescriptionThis animated image depicts another equilateral triangle, reinforcing the concept of equal sides and angles. Such animations help students visualize and understand the concept of congruence and symmetry in equilateral triangles. Incorporating animated math clip art into lessons enhances student engagement and understanding. The animation provides a clear and captivating representation of geometric concepts, making it easier for students to grasp and retain information. Teachers can use this clip art to facilitate discussions about the properties of equilateral triangles. |
Definition of a Triangle |
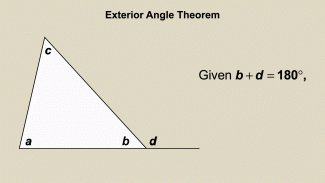
|
Animated Math Clip Art--Triangles--Exterior Angle Theorem 1 |
Animated Math Clip Art--Triangles--Exterior Angle Theorem 1TopicTriangles DescriptionThis animation illustrates the Exterior Angle Theorem, which states that the exterior angle of a triangle is equal to the sum of the two opposite interior angles. The animation dynamically shows the exterior angle being formed and highlights the relationship between the angles, making it easier for students to grasp this fundamental geometric theorem. |
Definition of a Triangle |
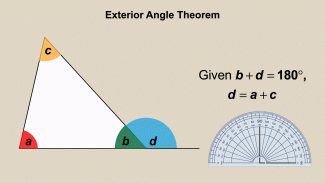
|
Animated Math Clip Art--Triangles--Exterior Angle Theorem 2 |
Animated Math Clip Art--Triangles--Exterior Angle Theorem 2TopicTriangles DescriptionThis animation further explores the Exterior Angle Theorem, reinforcing the concept that the exterior angle is the sum of the two non-adjacent interior angles. The animation provides a clear visual representation, helping students to see the theorem in action and understand its application in solving geometric problems. The color-coded angles are measured on a protractor. Using animated math clip art enhances student engagement and understanding by providing a dynamic and interactive way to learn. Teachers can use this animation to encourage students to explore and apply the theorem in various contexts. |
Definition of a Triangle |
|
Animated Math Clip Art--Triangles--Isosceles Triangles 1 |
Animated Math Clip Art--Triangles--Isosceles Triangles 1TopicTriangles DescriptionThis animation shows an isosceles triangle, characterized by two equal sides and two equal angles. The animation highlights these equal elements, helping students to identify and understand the properties of isosceles triangles. This visual aid is crucial for recognizing symmetry and congruence in geometry. Animated math clip art provides a captivating way to teach geometric concepts, making them more memorable and understandable for students. Teachers can use this animation to discuss the properties of isosceles triangles and their applications. |
Definition of a Triangle |
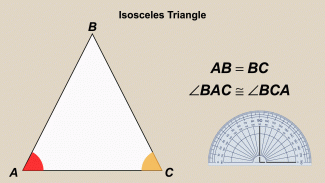
|
Animated Math Clip Art--Triangles--Isosceles Triangles 2 |
Animated Math Clip Art--Triangles--Isosceles Triangles 2TopicTriangles DescriptionThis animation provides another example of an isosceles triangle, emphasizing the equal sides and angles. The animation helps students to visualize and understand the characteristics of isosceles triangles, reinforcing their ability to identify these triangles in various contexts. The color-coded angles and sides are measured. Incorporating animated math clip art into lessons engages students and enhances their understanding of geometric concepts. Teachers can use this animation to encourage students to explore the properties and applications of isosceles triangles. |
Definition of a Triangle |
|
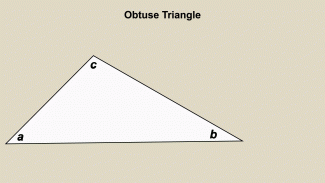
Animated Math Clip Art--Triangles--Obtuse Triangles 1 |
Animated Math Clip Art--Triangles--Obtuse Triangles 1TopicTriangles DescriptionThis animation depicts an obtuse triangle, where one angle is greater than 90 degrees. The animation highlights the obtuse angle, helping students to identify and understand the properties of obtuse triangles. This visual representation is essential for distinguishing obtuse triangles from other types. Animated math clip art is an effective tool for teaching geometric concepts, making them more engaging and comprehensible for students. Teachers can use this animation to discuss the properties and applications of obtuse triangles. |
Definition of a Triangle |
|
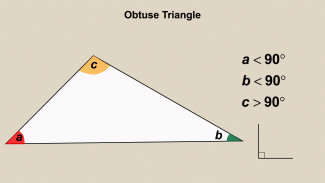
Animated Math Clip Art--Triangles--Obtuse Triangles 2 |
Animated Math Clip Art--Triangles--Obtuse Triangles 2TopicTriangles DescriptionThis animation illustrates another obtuse triangle, focusing on the angle greater than 90 degrees. The animation helps students to visualize and understand the characteristics of obtuse triangles, reinforcing their ability to identify these triangles in different scenarios. Using animated math clip art in teaching enhances student engagement and understanding by providing a dynamic and interactive learning experience. Teachers can use this animation to facilitate discussions about the properties of obtuse triangles. |
Definition of a Triangle |
|
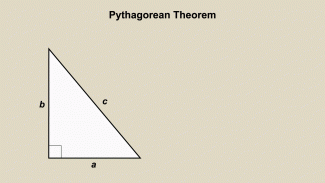
Animated Math Clip Art--Triangles--Pythagorean Theorem 1 |
Animated Math Clip Art--Triangles--Pythagorean Theorem 1TopicTriangles DescriptionThis animation demonstrates the Pythagorean Theorem, showing the relationship between the sides of a right triangle. The animation visually represents the theorem, illustrating how the square of the hypotenuse equals the sum of the squares of the other two sides. This helps students to understand and apply the theorem in solving problems. Animated math clip art is a powerful educational tool, providing a clear and engaging way to learn complex concepts. Teachers can use this animation to explain the Pythagorean Theorem and its applications in geometry. |
Definition of a Triangle |

|
Animated Math Clip Art--Triangles--Pythagorean Theorem 2 |
Animated Math Clip Art--Triangles--Pythagorean Theorem 2TopicTriangles DescriptionThis animation further explores the Pythagorean Theorem, reinforcing the concept with another example. The animation helps students to visualize the theorem in action, making it easier to understand and apply in various contexts. Incorporating animated math clip art into lessons engages students and enhances their understanding of mathematical concepts. Teachers can use this animation to encourage students to explore and apply the Pythagorean Theorem in different scenarios. Teacher’s Script: "Observe how the Pythagorean Theorem is applied in this triangle. How might this help us in real-world situations?" |
Definition of a Triangle |
|
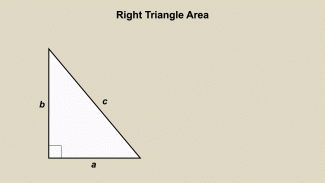
Animated Math Clip Art--Triangles--Right Triangle Area 1 |
Animated Math Clip Art--Triangles--Right Triangle Area 1TopicTriangles DescriptionThis animation shows how to calculate the area of a right triangle. The animation demonstrates the formula for area, emphasizing the base and height, and how they are used to find the area. This visual aid helps students understand the concept of area and its calculation in right triangles. Animated math clip art provides a dynamic way to teach mathematical concepts, making them more engaging and understandable for students. Teachers can use this animation to explain the concept of area and its application in geometry. |
Definition of a Triangle |
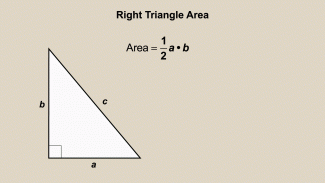
|
Animated Math Clip Art--Triangles--Right Triangle Area 2 |
Animated Math Clip Art--Triangles--Right Triangle Area 2TopicTriangles DescriptionThis animation illustrates another example of calculating the area of a right triangle. The animation reinforces the concept of using the base and height to determine the area, helping students to understand and apply the formula in various contexts. Using animated math clip art in teaching enhances student engagement and understanding by providing a clear and interactive learning experience. Teachers can use this animation to facilitate discussions about the concept of area and its applications. |
Definition of a Triangle |
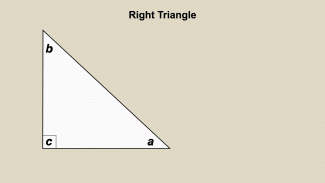
|
Animated Math Clip Art--Triangles--Right Triangles 1 |
Animated Math Clip Art--Triangles--Right Triangles 1TopicTriangles DescriptionThis animation depicts a right triangle, characterized by one 90-degree angle. The animation highlights the right angle, helping students to identify and understand the properties of right triangles. This visual representation is essential for recognizing right triangles and their applications in geometry. Animated math clip art is an effective tool for teaching geometric concepts, making them more engaging and comprehensible for students. Teachers can use this animation to discuss the properties and applications of right triangles. |
Definition of a Triangle |
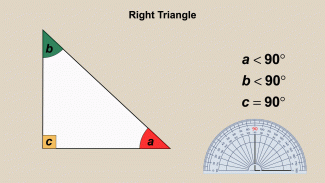
|
Animated Math Clip Art--Triangles--Right Triangles 2 |
Animated Math Clip Art--Triangles--Right Triangles 2TopicTriangles DescriptionThis animation provides another example of a right triangle, emphasizing the 90-degree angle. The animation helps students to visualize and understand the characteristics of right triangles, reinforcing their ability to identify these triangles in various contexts. Incorporating animated math clip art into lessons engages students and enhances their understanding of geometric concepts. Teachers can use this animation to encourage students to explore the properties and applications of right triangles. |
Definition of a Triangle |
|
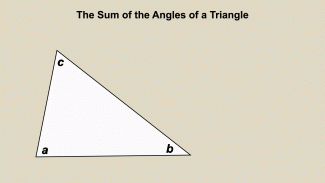
Animated Math Clip Art--Triangles--The Sum of the Angles of a Triangle |
Animated Math Clip Art--Triangles--The Sum of the Angles of a TriangleTopicTriangles DescriptionThis animation demonstrates the concept that the sum of the angles in a triangle is always 180 degrees. The animation visually shows how the angles add up to form a straight line, making it easier for students to understand this fundamental geometric principle. Animated math clip art provides a dynamic way to teach mathematical concepts, making them more engaging and understandable for students. Teachers can use this animation to explain the sum of angles in a triangle and its applications in geometry. |
Definition of a Triangle |
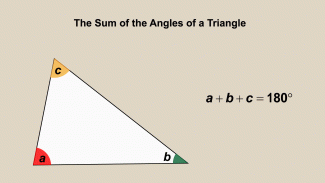
|
Animated Math Clip Art--Triangles--The Sum of the Angles of a Triangle 2 |
Animated Math Clip Art--Triangles--The Sum of the Angles of a Triangle 2TopicTriangles DescriptionThis animation demonstrates the concept that the sum of the angles in a triangle is always 180 degrees. The visual representation shows how the angles combine to form a straight line, reinforcing the understanding of this fundamental geometric principle. Animated math clip art is an effective educational tool as it visually demonstrates mathematical concepts, making them more accessible and engaging for students. By using this animation, teachers can help students visualize and understand the theorem, facilitating a deeper comprehension of triangle properties. |
Definition of a Triangle |
|
Animated Math Clip Art--Triangles--Triangle Area 1 |
Animated Math Clip Art--Triangles--Triangle Area 1TopicTriangles DescriptionThis animation illustrates how to calculate the area of a triangle using the formula 1/2 × base × height. The animation highlights the base and height, helping students understand the components needed to find the area of a triangle. Using animated math clip art enhances student engagement and understanding by providing a dynamic and interactive way to learn. Teachers can use this animation to encourage students to explore and apply the formula in various contexts. Teacher’s Script: "Watch how we calculate the area of this triangle. What do we need to know to find the area?" |
Definition of a Triangle |
|
Animated Math Clip Art--Triangles--Triangle Area 2 |
Animated Math Clip Art--Triangles--Triangle Area 2TopicTriangles DescriptionThis animation provides another example of calculating the area of a triangle, reinforcing the use of the base and height in the formula 1/2 × base × height. The animation helps students visualize and understand how to apply this formula to determine the area. Incorporating animated math clip art into lessons engages students and enhances their understanding of mathematical concepts. Teachers can use this animation to facilitate discussions about the concept of area and its applications. Teacher’s Script: "Look at how we find the area of this triangle. How can we use this knowledge in different situations?" |
Definition of a Triangle |
|
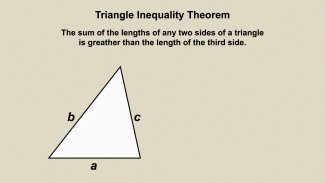
Animated Math Clip Art--Triangles--Triangle Inequality 1 |
Animated Math Clip Art--Triangles--Triangle Inequality 1TopicTriangles DescriptionThis animation illustrates the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. The animation visually demonstrates this principle, helping students to understand and apply it in geometric contexts. Animated math clip art provides a clear and engaging way to learn complex concepts. Teachers can use this animation to explain the Triangle Inequality Theorem and its applications in geometry. |
Definition of a Triangle |
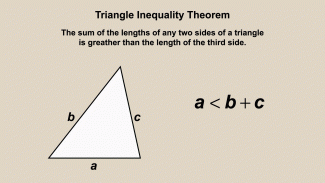
|
Animated Math Clip Art--Triangles--Triangle Inequality 2 |
Animated Math Clip Art--Triangles--Triangle Inequality 2TopicTriangles DescriptionThis animation provides another demonstration of the Triangle Inequality Theorem, reinforcing the concept that the sum of the lengths of any two sides must exceed the length of the third side. The animation helps students visualize and apply this theorem in various scenarios. Using animated math clip art in teaching enhances student engagement and understanding by providing a dynamic and interactive learning experience. Teachers can use this animation to encourage students to explore the properties and applications of the Triangle Inequality Theorem. |
Definition of a Triangle |
|
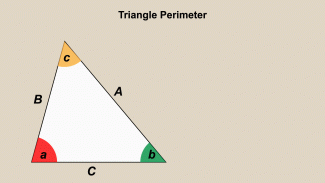
Animated Math Clip Art--Triangles--Triangle Perimeter 1 |
Animated Math Clip Art--Triangles--Triangle Perimeter 1TopicTriangles DescriptionThis animation shows how to calculate the perimeter of a triangle by summing the lengths of its sides. The animation highlights each side, helping students understand the concept of perimeter and its calculation in triangles. Animated math clip art provides a dynamic way to teach mathematical concepts, making them more engaging and understandable for students. Teachers can use this animation to explain the concept of perimeter and its application in geometry. Teacher’s Script: "Watch how we calculate the perimeter of this triangle. What do we need to know to find the perimeter?" |
Definition of a Triangle |
|
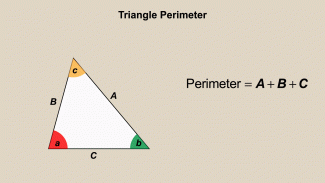
Animated Math Clip Art--Triangles--Triangle Perimeter 2 |
Animated Math Clip Art--Triangles--Triangle Perimeter 2TopicTriangles DescriptionThis animation provides another example of calculating the perimeter of a triangle, reinforcing the concept of summing the side lengths. The animation helps students visualize and understand how to determine the perimeter in different contexts. Incorporating animated math clip art into lessons engages students and enhances their understanding of geometric concepts. Teachers can use this animation to facilitate discussions about the concept of perimeter and its applications. Teacher’s Script: "Look at how we find the perimeter of this triangle. How can we use this knowledge in different situations?" |
Definition of a Triangle |

|
Closed Captioned Video: Geometry Applications: Triangles |
Closed Captioned Video: Geometry Applications: TrianglesTopicTriangles |
Definition of a Triangle and Applications of Triangles |

|
Closed Captioned Video: Geometry Applications: Triangles, 1 |
Closed Captioned Video: Geometry Applications: Triangles, 1TopicTriangles |
Definition of a Triangle and Applications of Triangles |

|
Closed Captioned Video: Geometry Applications: Triangles, 2 |
Closed Captioned Video: Geometry Applications: Triangles, 2TopicTriangles |
Definition of a Triangle and Applications of Triangles |

|
Closed Captioned Video: Geometry Applications: Triangles, 3 |
Closed Captioned Video: Geometry Applications: Triangles, 3TopicTriangles |
Definition of a Triangle and Applications of Triangles |

|
Definition--Geometry Basics--Base |
BaseTopicGeometry Basics DefinitionThe bottom side of a geometric figure from which the height is perpendicular. DescriptionThe base in geometry refers to the bottom side of a geometric figure, from which the height is measured perpendicularly. This concept is crucial in calculating the area and volume of various shapes. For instance, the area of a triangle is calculated using the formula 1/2 × base × height. Understanding the base is essential for solving problems related to dimensions and properties of geometric figures. |
Definition of a Triangle |
|
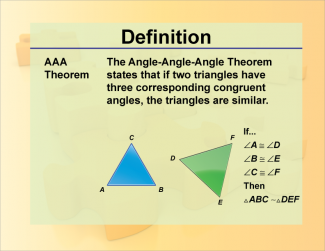
Definition--Theorems and Postulates--AAA Theorem |
Definition--Theorems and Postulates--AAA Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
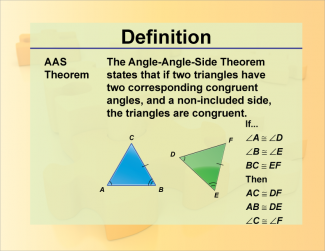
Definition--Theorems and Postulates--AAS Theorem |
Definition--Theorems and Postulates--AAS Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
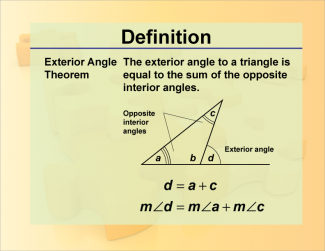
Definition--Theorems and Postulates--Exterior Angle Theorem |
Definition--Theorems and Postulates--Exterior Angle Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
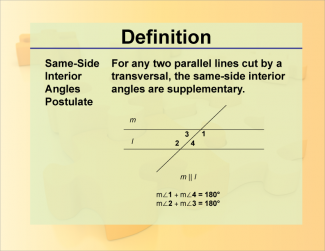
Definition--Theorems and Postulates--Same-Side Interior Angles Postulate |
Definition--Theorems and Postulates--Same-Side Interior Angles Postulate
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
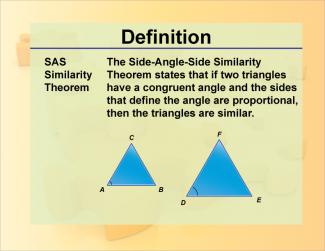
Definition--Theorems and Postulates--SAS Similarity Theorem |
Definition--Theorems and Postulates--SAS Similarity Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
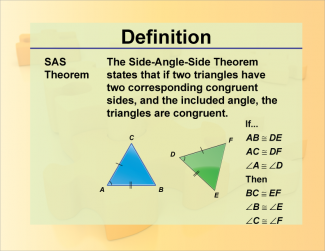
Definition--Theorems and Postulates--SAS Theorem |
Definition--Theorems and Postulates--SAS Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
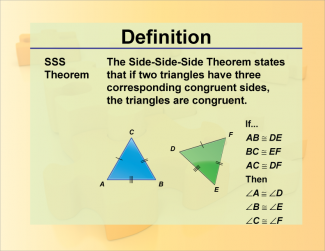
Definition--Theorems and Postulates--SSS Postulate |
Definition--Theorems and Postulates--SSS Postulate
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |

|
Definition--Triangle Concepts--3-4-5 Right Triangle |
3-4-5 Right TriangleTopicTriangles DefinitionA 3-4-5 right triangle is a right triangle with side lengths in the ratio 3:4:5. DescriptionThe 3-4-5 right triangle is a specific type of right triangle where the sides are in a simple integer ratio, making it a Pythagorean triple. This triangle is significant in geometry because it provides a simple example of the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides: 32 + 42 = 52 |
Definition of a Triangle |

|
Definition--Triangle Concepts--30-60-90 Right Triangles |
30-60-90 Right TrianglesTopicTriangles DefinitionA 30-60-90 right triangle is a right triangle with angles of 30 degrees, 60 degrees, and 90 degrees. DescriptionThe 30-60-90 triangle is a special right triangle characterized by its angle measures. The sides of this triangle are in the ratio 1:√3:2, meaning the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is √3 times the length of the shorter leg. This relationship can be derived using trigonometric principles and is fundamental in geometry. |
Definition of a Triangle |

|
Definition--Triangle Concepts--45-45-90 Right Triangles |
45-45-90 Right TrianglesTopicTriangles DefinitionA 45-45-90 right triangle is a right triangle with two 45-degree angles and one 90-degree angle. DescriptionThe 45-45-90 triangle is another special right triangle where the two legs are of equal length, and the hypotenuse is √2 times the length of each leg. This type of triangle is also known as an isosceles right triangle due to its equal legs. |
Definition of a Triangle |

|
Definition--Triangle Concepts--5-12-13 Right Triangle |
5-12-13 Right TriangleTopicTriangles DefinitionA 5-12-13 right triangle is a right triangle with side lengths in the ratio 5:12:13. DescriptionThe 5-12-13 right triangle is another example of a Pythagorean triple, where the sides satisfy the Pythagorean theorem: 52 + 122 = 132 This triangle is useful in various mathematical problems and real-world applications due to its simple integer side lengths. |
Definition of a Triangle |
|
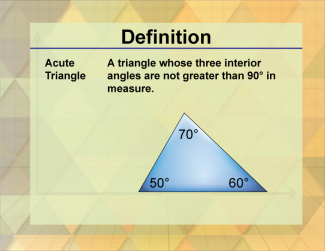
Definition--Triangle Concepts--Acute Triangle |
Acute TriangleTopicTriangles DefinitionAn acute triangle is a triangle where all three angles are less than 90 degrees. DescriptionAn acute triangle is characterized by having all its interior angles less than 90 degrees. This type of triangle is common in various geometric shapes and structures, making it a fundamental concept in geometry. Acute triangles are significant in real-world applications, such as in the design of roofs, bridges, and other structures where stability and aesthetic appeal are important. The properties of acute triangles, such as their angles and side lengths, are used to ensure that structures are both functional and visually pleasing. |
Definition of a Triangle |
|
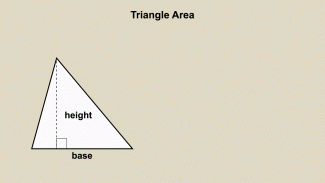
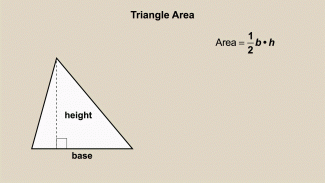
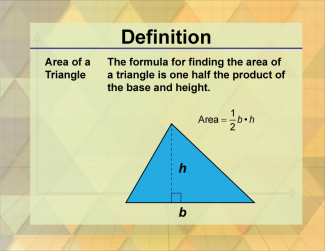
Definition--Triangle Concepts--Area of a Triangle |
Area of a TriangleTopicTriangles DefinitionThe area of a triangle is the amount of space enclosed by the triangle, calculated as 1/2 × base × height. DescriptionThe area of a triangle is a fundamental concept in geometry, representing the amount of space enclosed by the triangle's sides. The formula for the area is 1/2 × base × height where the base is one side of the triangle, and the height is the perpendicular distance from the base to the opposite vertex. |
Definition of a Triangle |
|
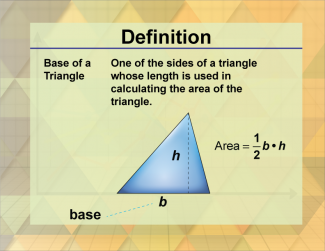
Definition--Triangle Concepts--Base of a Triangle |
Base of a TriangleTopicTriangles DefinitionThe base of a triangle is any one of its sides, typically used as a reference for calculating area. DescriptionThe base of a triangle is an essential concept in geometry, as it serves as a reference side for various calculations, including the area of the triangle. The base can be any one of the triangle's sides, but it is usually chosen for convenience based on the problem at hand. |
Definition of a Triangle |
|
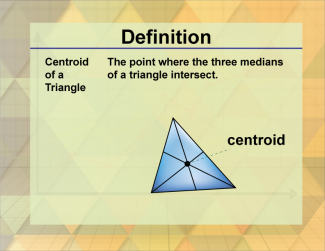
Definition--Triangle Concepts--Centroid of a Triangle |
Centroid of a TriangleTopicTriangles DefinitionThe centroid of a triangle is the point where its three medians intersect, often considered the triangle's center of mass. DescriptionThe centroid of a triangle is a significant point in geometry, representing the intersection of the triangle's medians. Each median is a line segment drawn from a vertex to the midpoint of the opposite side. The centroid is also known as the triangle's center of mass or balance point. |
Definition of a Triangle |
|
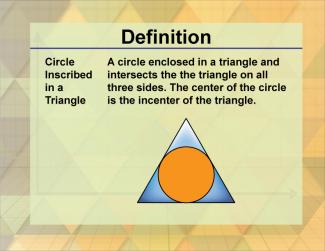
Definition--Triangle Concepts--Circle Inscribed In a Triangle |
Circle Inscribed In a TriangleTopicTriangles DefinitionA circle inscribed in a triangle is a circle that touches all three sides of the triangle from the inside. DescriptionAn inscribed circle in a triangle, also known as an incircle, is a circle that is tangent to all three sides of the triangle. The center of this circle is called the incenter, which is the point where the angle bisectors of the triangle intersect. |
Definition of a Triangle |
|
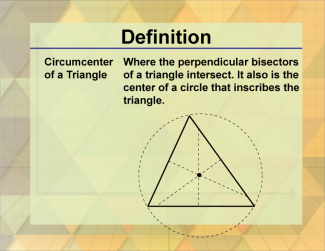
Definition--Triangle Concepts--Circumcenter of a Triangle |
Circumcenter of a TriangleTopicTriangles DefinitionThe circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, and it is the center of the triangle's circumcircle. DescriptionThe circumcenter of a triangle is a crucial concept in geometry, representing the point where the perpendicular bisectors of the triangle's sides intersect. This point is equidistant from all three vertices of the triangle, making it the center of the circumcircle, which is the circle that passes through all three vertices. |
Definition of a Triangle |
|
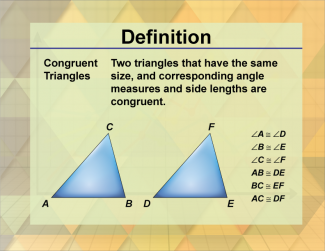
Definition--Triangle Concepts--Congruent Triangles |
Congruent TrianglesTopicTriangles DefinitionCongruent triangles are triangles that have the same size and shape, with corresponding sides and angles that are equal. DescriptionCongruent triangles are fundamental in geometry, representing triangles that are identical in size and shape. This means that all corresponding sides and angles of congruent triangles are equal. The concept of congruence is crucial for proving various geometric theorems and properties. |
Definition of a Triangle |
|
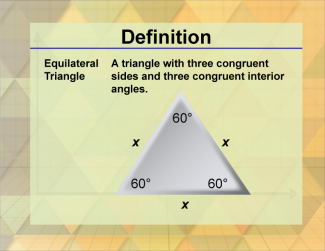
Definition--Triangle Concepts--Equilateral Triangle |
Equilateral TriangleTopicTriangles DefinitionAn equilateral triangle is a triangle with all three sides of equal length and all three angles equal to 60 degrees. DescriptionAn equilateral triangle is a special type of triangle where all three sides are of equal length, and all three interior angles are equal to 60 degrees. This symmetry makes equilateral triangles unique and significant in various geometric constructions. |
Definition of a Triangle |
|
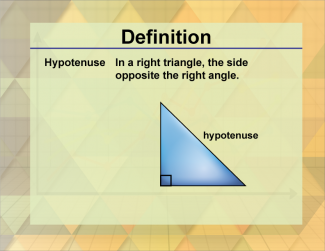
Definition--Triangle Concepts--Hypotenuse |
HypotenuseTopicTriangles DefinitionThe hypotenuse is the longest side of a right triangle, opposite the right angle. DescriptionThe hypotenuse is a crucial concept in geometry, representing the longest side of a right triangle, opposite the right angle. The Pythagorean theorem relates the hypotenuse to the other two sides of the triangle: a2 + b2 = c2 where c is the hypotenuse. |
Definition of a Triangle |
|
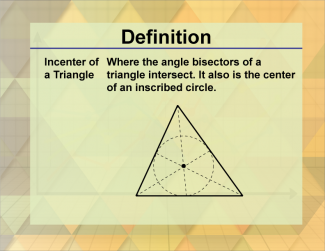
Definition--Triangle Concepts--Incenter of a Triangle |
Incenter of a TriangleTopicTriangles DefinitionThe incenter of a triangle is the point where the angle bisectors of the triangle intersect, and it is the center of the triangle's incircle. DescriptionThe incenter of a triangle is a significant point in geometry, representing the intersection of the triangle's angle bisectors. This point is equidistant from all three sides of the triangle, making it the center of the incircle, which is the circle that is tangent to all three sides. |
Definition of a Triangle |