Illustrative Math Alignment: Grade 6 Unit 8

Data Sets and Distributions

Lesson 2: Statistical Questions

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Nodes
Definition--Charts and Graphs--Categorical Data	Definition--Charts and Graphs--Categorical Data This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Continuous Data	Definition--Charts and Graphs--Continuous Data This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
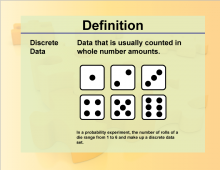
Definition--Charts and Graphs--Discrete Data	Definition--Charts and Graphs--Discrete Data This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
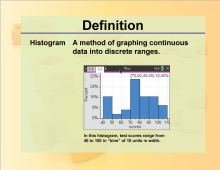
Definition--Charts and Graphs--Histogram	Definition--Charts and Graphs--Histogram This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Two-Way Frequency Table	Definition--Charts and Graphs--Two-Way Frequency Table This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
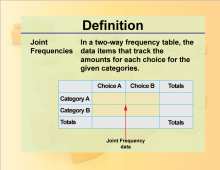
Definition--Charts and Graphs--Joint Frequencies	Definition--Charts and Graphs--Joint Frequencies This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
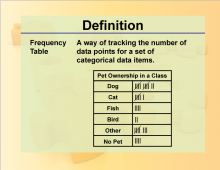
Definition--Charts and Graphs--Frequency Table	Definition--Charts and Graphs--Frequency Table This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Scaled Pictograph	Definition--Charts and Graphs--Scaled Pictograph This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Pictograph	Definition--Charts and Graphs--Pictograph This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Stem-and-Leaf Plot	Definition--Charts and Graphs--Stem-and-Leaf Plot This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
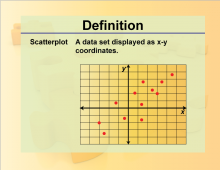
Definition--Charts and Graphs--Scatterplot	Definition--Charts and Graphs--Scatterplot This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
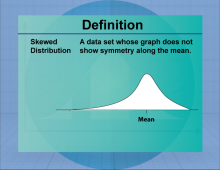
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Histogram	Histogram Topic Statistics Definition A histogram is a graphical representation of data distribution using bars of different heights. Description Histograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Mode of Categorical Data	Mode of Categorical Data Topic Statistics Definition The mode of categorical data is the most frequent item in a categorical data set. Description The Mode of Categorical Data is useful for finding the most frequent data item used with non-numerical data. For example, preferences for discrete characteristics can result in a mode.	Data Analysis
Definition--Measures of Central Tendency--Median of an Even Data Set	Median of an Even Data Set Topic Statistics Definition The median of an even data set is the mean of two of the terms. Description The Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms.	Data Analysis
Definition--Measures of Central Tendency--Median of an Odd Data Set	Median of an Odd Data Set Topic Statistics Definition The median of an odd data set is one of the terms in the data set. Description The Median is the middle term of a data set. If the data set consists of an odd number of terms, no matter how many terms there are, the Median will be the middle term of that set. In mathematics education, understanding median of an odd data set is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
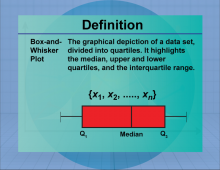
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
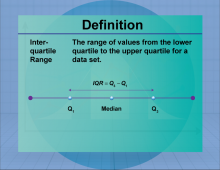
Definition--Measures of Central Tendency--Interquartile Range	Interquartile Range Topic Statistics Definition The interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. Description The IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
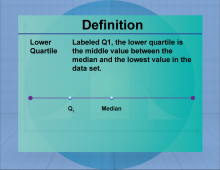
Definition--Measures of Central Tendency--Lower Quartile	Lower Quartile Topic Statistics Definition The lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. Description The lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
Definition--Measures of Central Tendency--Average Speed	Average Speed Topic Statistics Definition Average speed is the total distance traveled divided by the total time taken. Description This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.	Data Analysis
Definition--Measures of Central Tendency--Weighted Mean	Weighted Mean Topic Statistics Definition The weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. Description The weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Average	Average Topic Statistics Definition The average is a measure of central tendency, calculated by dividing the sum of values by their count. Description In statistics, the average is crucial for analyzing data sets, revealing trends, and providing insight into overall performance. It’s applicable in various fields, from school grades to business metrics. For example, if a student scores 80, 90, and 100 on three exams, the average can be calculated as follows: Average = (80 + 90 + 100) / 3 = 90. The average is essential in math education as it forms a foundational concept for more advanced statistical analyses.	Data Analysis
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 5	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 5 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
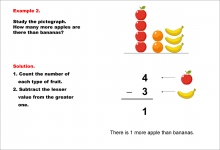
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 1	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 1 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 2	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 2 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 3	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 3 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 4	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 4 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 6	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 6 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 7	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 7 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 9	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 9 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
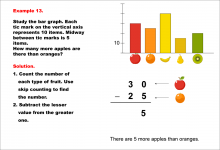
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 13	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 13 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
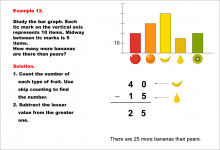
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 12	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 12 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
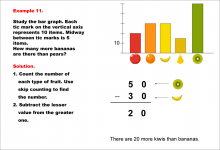
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 11	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 11 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
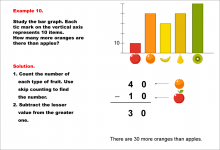
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 8	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 8 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
Math Example--Charts, Graphs, and Plots--Reading and Interpreting Scaled Graphs--Example 10	Math Example--Charts, Graphs, and Plots-- Reading and Interpreting Scaled Graphs--Example 10 In this set of math examples, analyze the behavior of different scatterplots. This includes linear and quadratic models.	Subtraction Facts to 100 and Data Analysis
Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability, 1	Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability, Segment 1 In this Investigation we explore uncertainty and randomness. This video is Segment 1 of a 4 segment series related to Data Analysis and Probability. Segments 1 and 2 are grouped together.	Data Analysis and Data Gathering
Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability, 3	Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability, Segment 3 In this Investigation we look at real-world data involving endangered wolf populations. This video is Segment 3 of a 4 segment series related to Data Analysis and Probability. Segments 3 and 4 are grouped together.	Data Analysis and Data Gathering
Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability	Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability What are the two meanings of statistics? What does it really mean that an event has a 50% probability of occurring? Why are data analysis and probability always taught together? Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video answers these questions and addresses fundamental concepts such as the law of large numbers and the notion of regression analysis. Both engaging investigations are based on true stories and real data, utilize different Nspire applications, and model the seamless connection among various problem representations. Concepts explored: statistics, data analysis, regression analysis.	Data Analysis and Data Gathering
Closed Captioned Video: Algebra Applications: Variables and Equations, 2	Closed Captioned Video: Algebra Applications: Variables and Equations, 2 Topic Equations Description The video investigates the geometry of river meanders using the concept of the meander ratio, calculated as the ratio of a river’s sinuous length to its straight-line length. It uses a TI-Nspire calculator to simulate river paths and compute ratios. Key vocabulary includes meander ratio, sinuous length, and geometric modeling. Applications highlight the mathematical modeling of natural phenomena and the occurrence of pi in nature.	Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions