
Illustrative Math Alignment: Grade 7 Unit 2
Introducing Proportional Relationships
Lesson 10: Introducing Graphs of Proportional Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
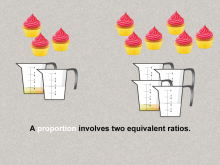
Math Clip Art--Ratios, Proportions, Percents--Proportions 02 | Math Clip Art--Ratios, Proportions, Percents--Proportions 02TopicRatios, Proportions, and Percents DescriptionThis image illustrates proportions using two equivalent ratios, represented by measuring cups and cupcakes. It simplifies proportions to relatable everyday examples. It connects proportions to practical examples, emphasizing the real-world relevance. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 02 | Math Clip Art--Ratios, Proportions, Percents--Proportions 02TopicRatios, Proportions, and Percents DescriptionThis image illustrates proportions using two equivalent ratios, represented by measuring cups and cupcakes. It simplifies proportions to relatable everyday examples. It connects proportions to practical examples, emphasizing the real-world relevance. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 03 | Math Clip Art--Ratios, Proportions, Percents--Proportions 03TopicRatios, Proportions, and Percents DescriptionThis image uses coins to demonstrate proportions. The image compares groups of quarters and nickels to highlight equivalent ratios (3:1 and 6:2). It solidifies the concept of equivalent ratios through another real-life example, reinforcing the idea. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 03 | Math Clip Art--Ratios, Proportions, Percents--Proportions 03TopicRatios, Proportions, and Percents DescriptionThis image uses coins to demonstrate proportions. The image compares groups of quarters and nickels to highlight equivalent ratios (3:1 and 6:2). It solidifies the concept of equivalent ratios through another real-life example, reinforcing the idea. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 04 | Math Clip Art--Ratios, Proportions, Percents--Proportions 04TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportions through a scale model example, comparing the height and width ratios of the Eiffel Tower in two scales. It highlights the application of proportions in scaling and models, bridging abstract and practical understanding. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 04 | Math Clip Art--Ratios, Proportions, Percents--Proportions 04TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportions through a scale model example, comparing the height and width ratios of the Eiffel Tower in two scales. It highlights the application of proportions in scaling and models, bridging abstract and practical understanding. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
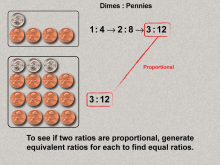
Math Clip Art--Ratios, Proportions, Percents--Proportions 05 | Math Clip Art--Ratios, Proportions, Percents--Proportions 05TopicRatios, Proportions, and Percents DescriptionThis image shows proportionality between dimes and pennies using equivalent ratios (1:4 and 3:12). Mathematical steps verify proportionality. It introduces proportional reasoning and calculation steps to ensure clarity in identifying proportional relationships. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 05 | Math Clip Art--Ratios, Proportions, Percents--Proportions 05TopicRatios, Proportions, and Percents DescriptionThis image shows proportionality between dimes and pennies using equivalent ratios (1:4 and 3:12). Mathematical steps verify proportionality. It introduces proportional reasoning and calculation steps to ensure clarity in identifying proportional relationships. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
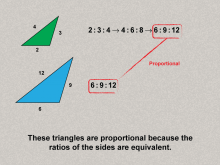
Math Clip Art--Ratios, Proportions, Percents--Proportions 06 | Math Clip Art--Ratios, Proportions, Percents--Proportions 06TopicRatios, Proportions, and Percents DescriptionThis image presents proportional triangles, with side lengths maintaining equivalent ratios (2:3:4 and 6:9:12). It demonstrates geometric applications of proportions, extending the concept to shapes and measurements. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 06 | Math Clip Art--Ratios, Proportions, Percents--Proportions 06TopicRatios, Proportions, and Percents DescriptionThis image presents proportional triangles, with side lengths maintaining equivalent ratios (2:3:4 and 6:9:12). It demonstrates geometric applications of proportions, extending the concept to shapes and measurements. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 07 | Math Clip Art--Ratios, Proportions, Percents--Proportions 07TopicRatios, Proportions, and Percents DescriptionThis image contrasts proportionality with non-proportional groups of coins (dimes and nickels). Ratios differ, clarifying when proportions do not exist. It explains non-proportionality to deepen understanding of proportional relationships. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 07 | Math Clip Art--Ratios, Proportions, Percents--Proportions 07TopicRatios, Proportions, and Percents DescriptionThis image contrasts proportionality with non-proportional groups of coins (dimes and nickels). Ratios differ, clarifying when proportions do not exist. It explains non-proportionality to deepen understanding of proportional relationships. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
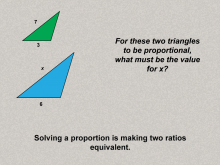
Math Clip Art--Ratios, Proportions, Percents--Proportions 08 | Math Clip Art--Ratios, Proportions, Percents--Proportions 08TopicRatios, Proportions, and Percents DescriptionThis image poses a question about proportional triangles, asking for the missing value (x) to maintain proportionality. It introduces problem-solving involving proportions, encouraging engagement and application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 08 | Math Clip Art--Ratios, Proportions, Percents--Proportions 08TopicRatios, Proportions, and Percents DescriptionThis image poses a question about proportional triangles, asking for the missing value (x) to maintain proportionality. It introduces problem-solving involving proportions, encouraging engagement and application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
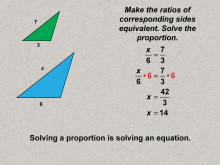
Math Clip Art--Ratios, Proportions, Percents--Proportions 09 | Math Clip Art--Ratios, Proportions, Percents--Proportions 09TopicRatios, Proportions, and Percents DescriptionThis image solves the posed proportion problem by finding the value of x using equivalent ratios (x/6 = 7/3). It breaks down the process of solving proportions, reinforcing mathematical reasoning. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 09 | Math Clip Art--Ratios, Proportions, Percents--Proportions 09TopicRatios, Proportions, and Percents DescriptionThis image solves the posed proportion problem by finding the value of x using equivalent ratios (x/6 = 7/3). It breaks down the process of solving proportions, reinforcing mathematical reasoning. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 10 | Math Clip Art--Ratios, Proportions, Percents--Proportions 10TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportionality in coins by calculating the number of nickels required for proportional groups (2/5 = 6/x). It closes the sequence with a real-world problem, consolidating the topic and providing a practical application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 10 | Math Clip Art--Ratios, Proportions, Percents--Proportions 10TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportionality in coins by calculating the number of nickels required for proportional groups (2/5 = 6/x). It closes the sequence with a real-world problem, consolidating the topic and providing a practical application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
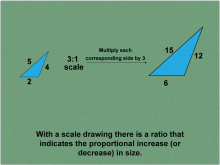
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
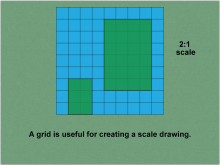
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
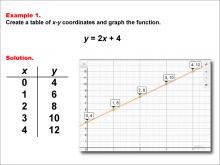
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 1 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 1TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 2x + 4. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 4), (1, 6), (2, 8), (3, 10), and (4, 12), illustrating how the y-value increases by 2 for each unit increase in x. |
Graphs of Linear Functions |
|
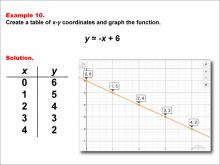
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 10 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 10TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -x + 6. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 6), (1, 5), (2, 4), (3, 3), and (4, 2), illustrating how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
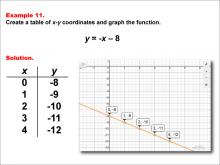
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 11 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 11TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = -x - 8. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -8), (1, -9), (2, -10), (3, -11), and (4, -12), showing how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
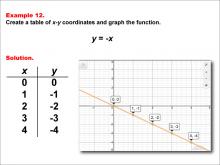
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 12 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 12TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = -x. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -1), (2, -2), (3, -3), and (4, -4), illustrating how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
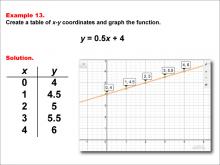
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 13 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 13TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0.5x + 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 4), (1, 4.5), (2, 5), (3, 5.5), and (4, 6), showing how the y-value increases by 0.5 for each unit increase in x. |
Graphs of Linear Functions |
|
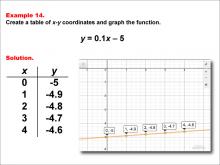
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 14 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 14TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 0.1x - 5. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, -5), (1, -4.9), (2, -4.8), (3, -4.7), and (4, -4.6), illustrating how the y-value increases by 0.1 for each unit increase in x. |
Graphs of Linear Functions |

|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 15 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 15TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0.2x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 0.2), (2, 0.4), (3, 0.6), and (4, 0.8), showing how the y-value increases by 0.2 for each unit increase in x. |
Graphs of Linear Functions |
|
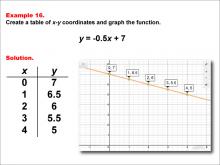
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 16 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 16TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -0.5x + 7. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 7), (1, 6.5), (2, 6), (3, 5.5), and (4, 5), illustrating how the y-value decreases by 0.5 for each unit increase in x. |
Graphs of Linear Functions |
|
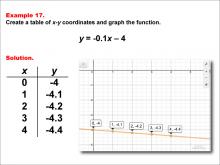
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 17 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 17TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = -0.1x - 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -4), (1, -4.1), (2, -4.2), (3, -4.3), and (4, -4.4), showing how the y-value decreases by 0.1 for each unit increase in x. |
Graphs of Linear Functions |
|
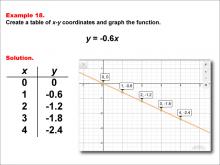
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 18 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 18TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -0.6x. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -0.6), (2, -1.2), (3, -1.8), and (4, -2.4), illustrating how the y-value decreases by 0.6 for each unit increase in x. |
Graphs of Linear Functions |
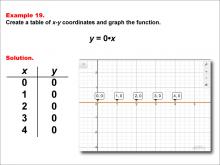
|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 19 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 19TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 0), (2, 0), (3, 0), and (4, 0), showing how the y-value remains constant at 0 for all values of x. |
Graphs of Linear Functions |
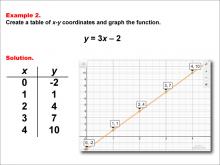
|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 2 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 2TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 3x - 2. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -2), (1, 1), (2, 4), (3, 7), and (4, 10), showing how the y-value increases by 3 for each unit increase in x. |
Graphs of Linear Functions |
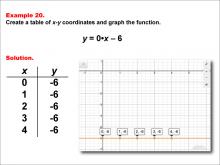
|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 20 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 20TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 0x - 6. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, -6), (1, -6), (2, -6), (3, -6), and (4, -6), illustrating how the y-value remains constant at -6 for all values of x. |
Graphs of Linear Functions |
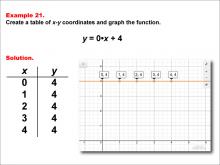
|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 21 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 21TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0 * x + 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 4), (1, 4), (2, 4), (3, 4), and (4, 4), showing how the y-value remains constant at 4 for all values of x. |
Graphs of Linear Functions |
|
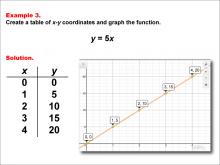
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 3 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 3TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = 5x. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, 5), (2, 10), (3, 15), and (4, 20), illustrating how the y-value increases by 5 for each unit increase in x. |
Graphs of Linear Functions |
|
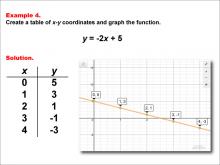
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 4 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 4TopicLinear Functions DescriptionThis example showcases the process of creating a table of x-y coordinates and graphing the linear function y = -2x + 5. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 5), (1, 3), (2, 1), (3, -1), and (4, -3), demonstrating how the y-value decreases by 2 for each unit increase in x. |
Graphs of Linear Functions |
|
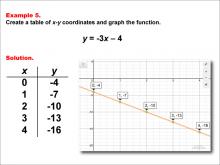
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 5 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 5TopicLinear Functions DescriptionThis example illustrates the creation of a table of x-y coordinates and the graphing of the linear function y = -3x - 4. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, -4), (1, -7), (2, -10), (3, -13), and (4, -16), showing how the y-value decreases by 3 for each unit increase in x. |
Graphs of Linear Functions |
|
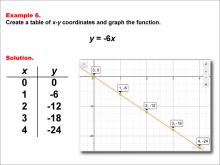
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 6 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 6TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -6x. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -6), (2, -12), (3, -18), and (4, -24), illustrating how the y-value decreases by 6 for each unit increase in x. |
Graphs of Linear Functions |
|
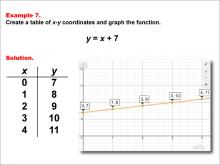
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 7 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 7TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = x + 7. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 7), (1, 8), (2, 9), (3, 10), and (4, 11), showing how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
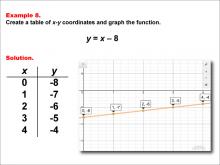
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 8 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 8TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = x - 8. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, -8), (1, -7), (2, -6), (3, -5), and (4, -4), illustrating how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
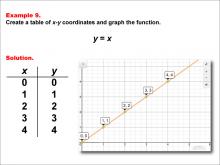
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 9 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 9TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 1), (2, 2), (3, 3), and (4, 4), showing how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
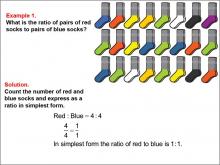
Math Example--Ratios and Rates--Example 1 | Math Example--Ratios and Rates--Example 1TopicRatios and Rates DescriptionThis math example focuses on understanding ratios using colored socks. The image displays a collection of red and blue socks, and students are asked to determine the ratio of red socks to blue socks. The solution demonstrates that there are 4 pairs of red socks and 4 pairs of blue socks, resulting in a ratio of 4 : 4, which simplifies to 1 : 1. |
Ratios and Rates |
|
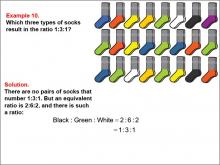
Math Example--Ratios and Rates--Example 10 | Math Example--Ratios and Rates--Example 10TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 3 : 1. |
Ratios and Rates |
|
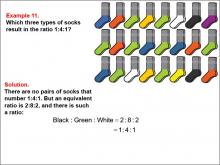
Math Example--Ratios and Rates--Example 11 | Math Example--Ratios and Rates--Example 11TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 4 : 1. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 12 | Math Example--Ratios and Rates--Example 12TopicRatios and Rates DescriptionThis example explores the concept of similar triangles using ratios. The image shows a right triangle with sides labeled as 9, 12, and 15 units. Students are asked to determine if this triangle is similar to a standard 3-4-5 Pythagorean triplet triangle. Understanding similar triangles is an important application of ratios in geometry. This example demonstrates how ratios can be used to compare the sides of triangles and determine similarity. By scaling the sides of a known triangle (3-4-5) and comparing them to the given triangle, students can see how ratios maintain proportionality in similar shapes. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 13 | Math Example--Ratios and Rates--Example 13TopicRatios and Rates DescriptionThis example focuses on verifying the similarity of triangles using ratios. The image shows a right triangle with sides labeled 25, 60, and 65 units. Students are guided through a step-by-step process to determine if this triangle is similar to a 5-12-13 right triangle. |
Ratios and Rates |