
Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 2: Adjacent Angles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Example--Area and Perimeter--Triangles: Example 18 | Math Example--Area and Perimeter--Triangles: Example 18TopicGeometry DescriptionThis example combines the concept of a 3-4-5 right triangle with algebraic expressions. The triangle's sides are labeled as 3(x + 4), 4(x + 4), and 5(x + 4). Students are challenged to express the area formula using these algebraic terms, applying their knowledge of both special right triangles and algebraic manipulation. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 19 | Math Example--Area and Perimeter--Triangles: Example 19TopicGeometry DescriptionThis example focuses on calculating the area of a right triangle with sides 5, 12, and 13 units. Students are guided through applying the area formula to this specific case, which involves a right triangle with integer side lengths that satisfy the Pythagorean theorem. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 2 | Math Example--Area and Perimeter--Triangles: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a scalene triangle's area using algebraic expressions. The triangle has sides labeled x, y, z, with a height labeled w from the base x. To find the area, we use the formula A = 1/2 * b * h. In this case, A = 1/2 * x * w = xw / 2. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 20 | Math Example--Area and Perimeter--Triangles: Example 20TopicGeometry DescriptionThis example combines the concept of a 5-12-13 right triangle with algebraic expressions. The triangle's sides are labeled as 5(x - 7), 12(x - 7), and 13(x - 7). Students are challenged to express the area formula using these algebraic terms, applying their knowledge of both special right triangles and algebraic manipulation. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 21 | Math Example--Area and Perimeter--Triangles: Example 21TopicGeometry DescriptionThis example introduces the concept of perimeter calculation for a scalene triangle. The triangle has sides measuring 5, 7, and 9 units. Students are guided through the process of calculating the perimeter by simply adding the lengths of all sides. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 22 | Math Example--Area and Perimeter--Triangles: Example 22TopicGeometry DescriptionThis example introduces the concept of perimeter calculation for a scalene triangle using algebraic expressions. The triangle has sides labeled x, y, and z. Students are guided through the process of expressing the perimeter using these variables. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 23 | Math Example--Area and Perimeter--Triangles: Example 23TopicGeometry DescriptionThis example focuses on calculating the perimeter of an acute triangle with specific side lengths. The triangle has sides measuring 10, 11, and 12 units, with angles of 50 and 60 degrees. Students are guided through the process of adding these side lengths to find the perimeter. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 24 | Math Example--Area and Perimeter--Triangles: Example 24TopicGeometry DescriptionThis example combines the concept of perimeter calculation for an acute triangle with algebraic expressions. The triangle has sides labeled as x - 3, x - 4, and x. Students are challenged to express the perimeter formula using these algebraic terms, applying their knowledge of both geometry and algebraic manipulation. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 25 | Math Example--Area and Perimeter--Triangles: Example 25TopicGeometry DescriptionThis example focuses on calculating the perimeter of an obtuse triangle with specific side lengths. The triangle has sides measuring 15, 6, and 18 units, with an obtuse angle of 120 degrees. Students are guided through the process of adding these side lengths to find the perimeter. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 26 | Math Example--Area and Perimeter--Triangles: Example 26TopicGeometry DescriptionThis example combines the concept of perimeter calculation for an obtuse triangle with algebraic expressions. The triangle has sides labeled as x + 1, x + 2, and x + 4, with an obtuse angle of 120 degrees. Students are challenged to express the perimeter formula using these algebraic terms, applying their knowledge of both geometry and algebraic manipulation. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 27 | Math Example--Area and Perimeter--Triangles: Example 27TopicGeometry DescriptionThis example focuses on calculating the perimeter of an isosceles triangle with specific side lengths. The triangle has two equal sides measuring 10 units and a base of 8 units. Students are guided through the process of adding these side lengths to find the perimeter. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 28 | Math Example--Area and Perimeter--Triangles: Example 28TopicGeometry DescriptionThis example combines the concept of perimeter calculation for an isosceles triangle with algebraic expressions. The triangle has two equal sides labeled as x + 4 and a base of x - 3. Students are challenged to express the perimeter formula using these algebraic terms, applying their knowledge of both geometry and algebraic manipulation. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 29 | Math Example--Area and Perimeter--Triangles: Example 29TopicGeometry DescriptionThis example focuses on calculating the perimeter of an equilateral triangle with specific side lengths. The triangle has all sides measuring 15 units. Students are guided through the process of adding these side lengths to find the perimeter, emphasizing the simplicity of calculations for equilateral triangles. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 3 | Math Example--Area and Perimeter--Triangles: Example 3TopicGeometry DescriptionThis example demonstrates how to calculate the area of an acute triangle. The triangle has angles labeled as 50° and 60°, with a base measuring 12 units and a height of 8 units. To find the area, we use the formula A = 1/2 * b * h. In this case, A = 1/2 * 12 * 8 = 48 square units. Understanding the area of triangles is a fundamental concept in geometry that applies to various real-world situations. This collection of examples helps students visualize different types of triangles and compute their areas accurately using given dimensions. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 30 | Math Example--Area and Perimeter--Triangles: Example 30TopicGeometry DescriptionThis example combines the concept of perimeter calculation for an equilateral triangle with algebraic expressions. The triangle has all sides labeled as 2x + 3. Students are challenged to express the perimeter formula using this algebraic term, applying their knowledge of both geometry and algebraic manipulation. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 31 | Math Example--Area and Perimeter--Triangles: Example 31TopicGeometry DescriptionThis example demonstrates the process of finding the perimeter of a right triangle when only two sides are given. The triangle has sides measuring 7 and 12 units. Students are guided through using the Pythagorean Theorem to find the length of the hypotenuse before calculating the perimeter. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 32 | Math Example--Area and Perimeter--Triangles: Example 32TopicGeometry DescriptionThis example demonstrates the process of finding the perimeter of a right triangle with algebraic expressions for its sides. The triangle has legs labeled as x - 2 and 2x. Students are guided through using the Pythagorean Theorem to find the hypotenuse and then calculating the perimeter using algebraic manipulation. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 33 | Math Example--Area and Perimeter--Triangles: Example 33TopicGeometry DescriptionThis example focuses on calculating the perimeter of an isosceles right triangle. The triangle has two equal sides of length 12 units and angles of 45 degrees. Students are guided through the process of using the Pythagorean Theorem to find the hypotenuse and then calculating the perimeter. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 34 | Math Example--Area and Perimeter--Triangles: Example 34TopicGeometry DescriptionThis example combines the concept of isosceles right triangles with algebraic expressions. The triangle has two equal sides labeled as x + 2 and angles of 45 degrees. Students are challenged to use the Pythagorean Theorem to find the hypotenuse and then express the perimeter using algebraic terms. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 35 | Math Example--Area and Perimeter--Triangles: Example 35TopicGeometry DescriptionThis example focuses on calculating the perimeter of a 30-60-90 right triangle. The triangle has sides of 12 and 24 units, with angles of 30 and 60 degrees. Students are guided through the process of using the Pythagorean Theorem to find the third side and then calculating the perimeter. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 36 | Math Example--Area and Perimeter--Triangles: Example 36TopicGeometry DescriptionThis example combines the concept of 30-60-90 right triangles with algebraic expressions. The triangle has sides labeled as x - 10 and 2(x - 10), with angles of 30 and 60 degrees. Students are challenged to use the Pythagorean Theorem to find the third side and then express the perimeter using algebraic terms. |
Area and Perimeter of Triangles |
|
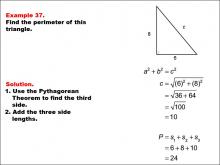
Math Example--Area and Perimeter--Triangles: Example 37 | Math Example--Area and Perimeter--Triangles: Example 37TopicGeometry DescriptionThis example demonstrates the process of finding the perimeter of a right triangle with sides of 6 and 8 units. Students are guided through using the Pythagorean Theorem to find the hypotenuse and then calculating the perimeter by adding all three sides. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 38 | Math Example--Area and Perimeter--Triangles: Example 38TopicGeometry DescriptionThis example combines the concept of right triangle perimeter with algebraic expressions. The triangle has sides labeled as 3(x + 4) and 4(x + 4). Students are challenged to use the Pythagorean Theorem to find the hypotenuse and then express the perimeter using algebraic terms. |
Area and Perimeter of Triangles |
|
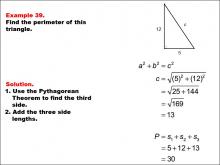
Math Example--Area and Perimeter--Triangles: Example 39 | Math Example--Area and Perimeter--Triangles: Example 39TopicGeometry DescriptionThis example demonstrates the process of finding the perimeter of a right triangle with sides of 5 and 12 units. Students are guided through using the Pythagorean Theorem to find the hypotenuse and then calculating the perimeter by adding all three sides. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 4 | Math Example--Area and Perimeter--Triangles: Example 4TopicGeometry DescriptionThis example introduces students to calculating the area of an acute triangle using algebraic expressions. The triangle has angles of 50 and 60 degrees, with the base labeled as x and the height as x - 4. Students are tasked with expressing the area formula using these variables. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 40 | Math Example--Area and Perimeter--Triangles: Example 40TopicGeometry DescriptionThis example combines the concept of right triangle perimeter with complex algebraic expressions. The triangle has sides labeled as 5(x + 10) and 12(x + 10). Students are challenged to use the Pythagorean Theorem to find the hypotenuse and then express the perimeter using algebraic terms. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 5 | Math Example--Area and Perimeter--Triangles: Example 5TopicGeometry DescriptionThis example demonstrates the calculation of area for an obtuse triangle. The triangle has a base of 15 units, a height of 8 units, and includes a 120-degree angle. Students are guided through the process of applying the area formula for this specific case. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 6 | Math Example--Area and Perimeter--Triangles: Example 6TopicGeometry DescriptionThis example combines the concepts of obtuse triangles and algebraic expressions. The triangle has a base of x + 1 and a height of x - 1, with a 120-degree angle. Students are challenged to express the area formula using these algebraic terms. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 7 | Math Example--Area and Perimeter--Triangles: Example 7TopicGeometry DescriptionThis example focuses on calculating the area of an isosceles triangle. The triangle has two equal angles of 65° and a base angle of 50°. The base is 8 units long, and the height is 10 units. Students are guided through applying the standard area formula to this specific case. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 8 | Math Example--Area and Perimeter--Triangles: Example 8TopicGeometry DescriptionThis example combines isosceles triangles with algebraic expressions. The triangle has two equal angles of 65° and a base angle of 50°. The base is expressed as x - 3, and the height as x + 3. Students are challenged to formulate the area using these algebraic terms. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 9 | Math Example--Area and Perimeter--Triangles: Example 9TopicGeometry DescriptionThis example focuses on calculating the area of an equilateral triangle. The triangle has all angles equal to 60°, a base of 12 units, and a height of 6√3 units. Students are guided through applying the area formula using these specific dimensions, which involve a square root. |
Area and Perimeter of Triangles |
|
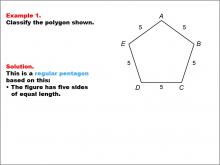
Math Example--Polygons--Polygon Classification: Example 1 | Math Example--Polygons--Polygon Classification: Example 1TopicPolygons DescriptionThis example showcases a pentagon with all sides labeled as 5. It demonstrates a regular pentagon, characterized by five sides of equal length. This visual representation helps students understand the concept of regular polygons and their defining characteristics. The topic of polygon classification is crucial in geometry. This collection of examples provides a comprehensive look at various types of pentagons, both regular and irregular. By examining different configurations of sides and angles, students can develop a deeper understanding of polygon properties and classification criteria. |
Definition of a Polygon |
|
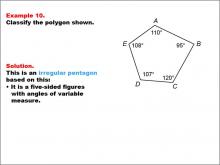
Math Example--Polygons--Polygon Classification: Example 10 | Math Example--Polygons--Polygon Classification: Example 10TopicPolygons DescriptionThis example showcases a pentagon labeled with vertices A, B, C, D, E, where the angles are marked as 110°, 95°, 120°, 107°, and 108°. It demonstrates an irregular pentagon based on the variation in angle measures, highlighting that regularity depends on both side lengths and angle measures. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples emphasizes the importance of both side lengths and angle measures in determining the regularity of pentagons. |
Definition of a Polygon |
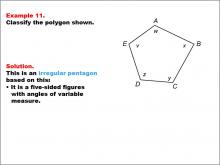
|
Math Example--Polygons--Polygon Classification: Example 11 | Math Example--Polygons--Polygon Classification: Example 11TopicPolygons DescriptionThis example presents a pentagon labeled with vertices A, B, C, D, E, where the sides are marked with variables w, x, y, z, and v. It illustrates an irregular pentagon by using different variables to represent potentially different side lengths, emphasizing that side length variation results in irregularity. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various types of pentagons, highlighting the importance of side length equality in determining regularity. |
Definition of a Polygon |
|
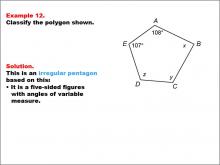
Math Example--Polygons--Polygon Classification: Example 12 | Math Example--Polygons--Polygon Classification: Example 12TopicPolygons DescriptionThis example features a pentagon labeled with vertices A, B, C, D, E, where the angles are marked as 108°, x, y, z, and 107°. It demonstrates an irregular pentagon based on the variation in angle measures, highlighting that regularity depends on all angles being equal. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples emphasizes the importance of angle measures in determining the regularity of pentagons, showing that even one different angle makes the polygon irregular. |
Definition of a Polygon |
|
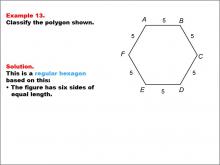
Math Example--Polygons--Polygon Classification: Example 13 | Math Example--Polygons--Polygon Classification: Example 13TopicPolygons DescriptionThis example showcases a hexagon with all sides labeled as 5, indicating equal length. It demonstrates a regular hexagon, characterized by six sides of equal length. This visual representation helps students understand the concept of regular polygons and their defining characteristics. The topic of polygon classification is crucial in geometry. This collection of examples provides a comprehensive look at various types of hexagons, both regular and irregular. By examining different configurations of sides and angles, students can develop a deeper understanding of polygon properties and classification criteria. |
Definition of a Polygon |
|
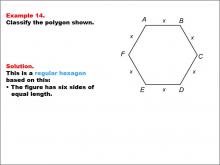
Math Example--Polygons--Polygon Classification: Example 14 | Math Example--Polygons--Polygon Classification: Example 14TopicPolygons DescriptionThis example presents a hexagon with all sides labeled as x, indicating equal length. It illustrates another instance of a regular hexagon, reinforcing the concept that a regular polygon has all sides of equal length, even when represented by a variable. Polygon classification is a fundamental topic in geometry that helps students understand the properties and characteristics of different shapes. This collection of examples provides a comprehensive overview of various hexagon types, allowing students to distinguish between regular and irregular polygons based on their side lengths and angle measures. |
Definition of a Polygon |
|
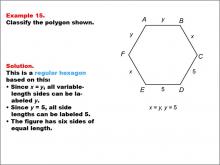
Math Example--Polygons--Polygon Classification: Example 15 | Math Example--Polygons--Polygon Classification: Example 15TopicPolygons DescriptionThis example features a hexagon with sides labeled y, x, and 5, showing that x = y = 5, making all sides equal in length. It demonstrates a regular hexagon by using a combination of variables and numeric values to represent equal side lengths. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights different ways to represent regular hexagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
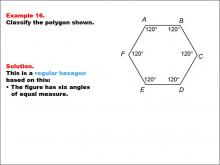
Math Example--Polygons--Polygon Classification: Example 16 | Math Example--Polygons--Polygon Classification: Example 16TopicPolygons DescriptionThis example showcases a hexagon with all interior angles labeled as 120 degrees, indicating equal angles. It demonstrates that a regular hexagon can be identified not only by equal side lengths but also by equal angle measures, reinforcing the dual criteria for regularity in polygons. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various aspects of regular hexagons, emphasizing both side length and angle measure as defining characteristics. |
Definition of a Polygon |
|
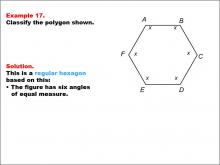
Math Example--Polygons--Polygon Classification: Example 17 | Math Example--Polygons--Polygon Classification: Example 17TopicPolygons DescriptionThis example presents a hexagon with six equal sides labeled as x and equal angles, indicating a regular hexagon. It reinforces the concept of a regular polygon by visually representing both the equality of all sides and angles. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples provides various representations of regular hexagons, emphasizing the importance of both side length and angle measure equality in classification. |
Definition of a Polygon |
|
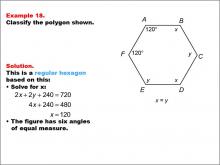
Math Example--Polygons--Polygon Classification: Example 18 | Math Example--Polygons--Polygon Classification: Example 18TopicPolygons DescriptionThis example features a hexagon with two angles labeled as 120 degrees and sides labeled x and y, where x = y. It demonstrates how to determine if a hexagon is regular by solving for the unknown angle measures and confirming equal side lengths. Polygon classification is a crucial topic in geometry that helps students distinguish between regular and irregular shapes. This collection of examples provides a comprehensive look at various types of hexagons, highlighting the importance of both angle measures and side lengths in determining regularity. |
Definition of a Polygon |
|
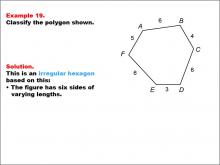
Math Example--Polygons--Polygon Classification: Example 19 | Math Example--Polygons--Polygon Classification: Example 19TopicPolygons DescriptionThis example showcases a hexagon with sides labeled with varying lengths: AB = 6, BC = 4, CD = 6, DE = 3, EF = 6, and FA = 5. It demonstrates an irregular hexagon, emphasizing that side length variation results in irregularity. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights the differences between regular and irregular hexagons, focusing on side length as a key determining factor. |
Definition of a Polygon |
|
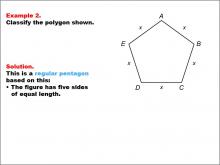
Math Example--Polygons--Polygon Classification: Example 2 | Math Example--Polygons--Polygon Classification: Example 2TopicPolygons DescriptionThis example presents a pentagon with all sides labeled as x, indicating equal length. It illustrates another instance of a regular pentagon, reinforcing the concept that a regular polygon has all sides of equal length. Polygon classification is a fundamental topic in geometry that helps students understand the properties and characteristics of different shapes. This collection of examples provides a comprehensive overview of various pentagon types, allowing students to distinguish between regular and irregular polygons based on their side lengths and angle measures. |
Definition of a Polygon |
|
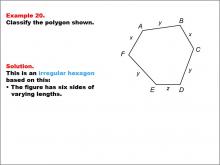
Math Example--Polygons--Polygon Classification: Example 20 | Math Example--Polygons--Polygon Classification: Example 20TopicPolygons DescriptionThis example presents a hexagon with sides labeled as x, y, and z, indicating varying lengths. It illustrates another case of an irregular hexagon, demonstrating that the presence of different variables for side lengths suggests irregularity. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various types of hexagons, emphasizing the importance of side length equality in determining regularity. |
Definition of a Polygon |
|
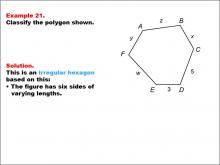
Math Example--Polygons--Polygon Classification: Example 21 | Math Example--Polygons--Polygon Classification: Example 21
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Polygon |
|
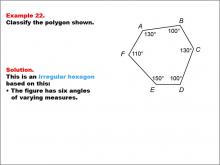
Math Example--Polygons--Polygon Classification: Example 22 | Math Example--Polygons--Polygon Classification: Example 22
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Polygon |
|
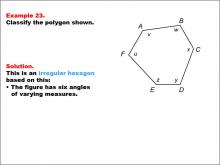
Math Example--Polygons--Polygon Classification: Example 23 | Math Example--Polygons--Polygon Classification: Example 23
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Polygon |
|
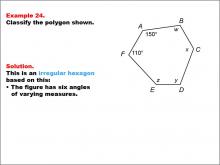
Math Example--Polygons--Polygon Classification: Example 24 | Math Example--Polygons--Polygon Classification: Example 24
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Polygon |
|
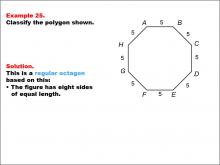
Math Example--Polygons--Polygon Classification: Example 25 | Math Example--Polygons--Polygon Classification: Example 25TopicPolygons DescriptionThis example showcases an octagon with all sides labeled as 5, indicating equal length. It demonstrates a regular octagon, characterized by eight sides of equal length. This visual representation helps students understand the concept of regular polygons and their defining characteristics. The topic of polygon classification is crucial in geometry. This collection of examples provides a comprehensive look at various types of octagons, both regular and irregular. By examining different configurations of sides and angles, students can develop a deeper understanding of polygon properties and classification criteria. |
Definition of a Polygon |
|
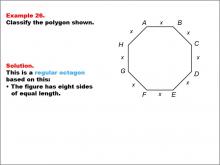
Math Example--Polygons--Polygon Classification: Example 26 | Math Example--Polygons--Polygon Classification: Example 26TopicPolygons DescriptionThis example presents an octagon with all sides labeled as x, indicating equal length. It illustrates another instance of a regular octagon, reinforcing the concept that a regular polygon has all sides of equal length, even when represented by a variable. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples provides various representations of regular octagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |