
Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 2: Adjacent Angles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
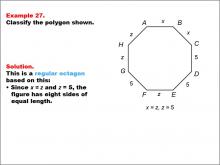
Math Example--Polygons--Polygon Classification: Example 27 | Math Example--Polygons--Polygon Classification: Example 27TopicPolygons DescriptionThis example features an octagon with sides labeled as x, z, and 5, showing that x = z = 5, indicating equal length for all sides. It demonstrates a regular octagon by using a combination of variables and numeric values to represent equal side lengths. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various aspects of regular octagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
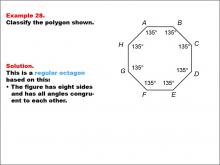
Math Example--Polygons--Polygon Classification: Example 28 | Math Example--Polygons--Polygon Classification: Example 28TopicPolygons DescriptionThis example showcases an octagon with all angles labeled as 135 degrees, indicating congruent angles. It demonstrates that a regular octagon can be identified not only by equal side lengths but also by equal angle measures, reinforcing the dual criteria for regularity in polygons. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights different aspects of regular octagons, emphasizing both side length and angle measure as defining characteristics. |
Definition of a Polygon |
|
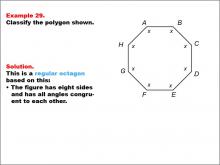
Math Example--Polygons--Polygon Classification: Example 29 | Math Example--Polygons--Polygon Classification: Example 29TopicPolygons DescriptionThis example presents an octagon with all angles labeled as "x," indicating a regular polygon. It illustrates a regular octagon by visually representing the equality of all angles using a single variable. This reinforces the concept that a regular polygon has all angles of equal measure. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various aspects of regular octagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
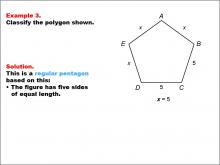
Math Example--Polygons--Polygon Classification: Example 3 | Math Example--Polygons--Polygon Classification: Example 3TopicPolygons DescriptionThis example features a pentagon with sides labeled x and two sides labeled as 5, with x = 5, demonstrating that all sides are equal. It reinforces the concept of a regular pentagon by showing how different notations can represent the same length. The study of polygon classification helps students develop critical thinking skills in geometry. This collection of examples illustrates various ways to represent and identify regular pentagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
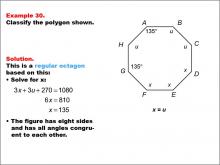
Math Example--Polygons--Polygon Classification: Example 30 | Math Example--Polygons--Polygon Classification: Example 30TopicPolygons DescriptionThis example features an octagon with angles labeled as 135° and angles labeled as "u" and "x." It demonstrates how to determine if an octagon is regular by solving for the unknown angle measures and confirming equal side lengths. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples provides insights into how partial information about angle measures and side lengths can be used to determine the regularity of octagons. |
Definition of a Polygon |
|
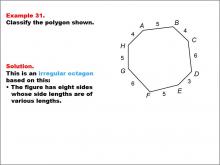
Math Example--Polygons--Polygon Classification: Example 31 | Math Example--Polygons--Polygon Classification: Example 31TopicPolygons DescriptionThis example showcases an irregular octagon with sides of varying lengths labeled as 4, 5, 6, and 3. It demonstrates that not all eight-sided figures are regular, emphasizing the importance of equal side lengths in the classification of regular polygons. Polygon classification is a crucial topic in geometry that helps students distinguish between regular and irregular shapes. This collection of examples provides a comprehensive look at various types of octagons, highlighting the differences between regular and irregular polygons based on side lengths. |
Definition of a Polygon |
|
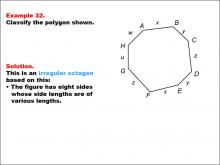
Math Example--Polygons--Polygon Classification: Example 32 | Math Example--Polygons--Polygon Classification: Example 32TopicPolygons DescriptionThis example presents an irregular octagon with sides labeled as w, x, y, z, and u, indicating varying lengths. It illustrates another case of an irregular octagon, demonstrating that the presence of different variables for side lengths suggests irregularity. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights the importance of considering side lengths when determining the regularity of octagons. |
Definition of a Polygon |
|
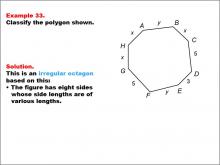
Math Example--Polygons--Polygon Classification: Example 33 | Math Example--Polygons--Polygon Classification: Example 33TopicPolygons DescriptionThis example features an octagon with sides labeled as x, y, 5, and 3. The sides are of varying lengths, indicating it is irregular. It demonstrates how a combination of variables and specific numeric values can be used to show irregularity in polygons. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides insights into how partial information about side lengths can be used to determine the irregularity of octagons. |
Definition of a Polygon |
|
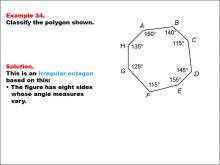
Math Example--Polygons--Polygon Classification: Example 34 | Math Example--Polygons--Polygon Classification: Example 34TopicPolygons DescriptionThis example showcases an octagon with angles labeled as 150°, 140°, 115°, 145°, 155°, 115°, 125°, and 135°. The angles vary, indicating it is irregular. It demonstrates that irregularity in polygons can be determined by examining angle measures alone. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights the importance of angle measures in determining the regularity of octagons, showing that even if side lengths are not given, angle information can be sufficient for classification. |
Definition of a Polygon |
|
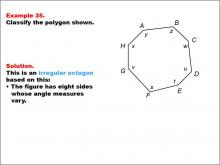
Math Example--Polygons--Polygon Classification: Example 35 | Math Example--Polygons--Polygon Classification: Example 35TopicPolygons DescriptionThis example presents an octagon with sides labeled as x, y, z, w, u, t, s, and v. The sides are of varying lengths and angles, indicating it is irregular. It illustrates how using different variables for both side lengths and angles can suggest irregularity in a polygon. Polygon classification is a crucial topic in geometry that helps students distinguish between regular and irregular shapes. This collection of examples provides a comprehensive look at various types of octagons, highlighting the importance of considering both side lengths and angle measures in determining regularity. |
Definition of a Polygon |
|
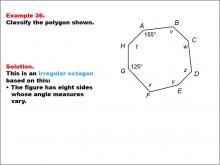
Math Example--Polygons--Polygon Classification: Example 36 | Math Example--Polygons--Polygon Classification: Example 36TopicPolygons DescriptionThis example features an octagon with angles labeled as 155° and 125°, and other angles labeled with variables t, v, w, x, y, and z. The angles vary, indicating it is irregular. It demonstrates how a combination of specific angle measures and variables can be used to show irregularity in polygons. Understanding polygon classification is essential in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights the importance of angle measures in determining the regularity of octagons, showing that even partial information can be sufficient for classification. |
Definition of a Polygon |
|
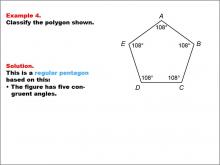
Math Example--Polygons--Polygon Classification: Example 4 | Math Example--Polygons--Polygon Classification: Example 4TopicPolygons DescriptionThis example showcases a pentagon with each angle labeled as 108 degrees, indicating congruent angles. It demonstrates that a regular pentagon can be identified not only by equal side lengths but also by equal angle measures. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights different aspects of regular pentagons, emphasizing both side length and angle measure as defining characteristics. |
Definition of a Polygon |
|
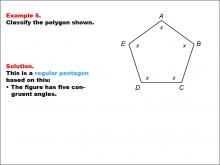
Math Example--Polygons--Polygon Classification: Example 5 | Math Example--Polygons--Polygon Classification: Example 5TopicPolygons DescriptionThis example presents a pentagon labeled with vertices A, B, C, D, and E, with each side marked with an "x" to indicate equal length. It reinforces the concept of a regular pentagon by visually representing the equality of all sides. Polygon classification is a fundamental topic in geometry that helps students understand the properties and relationships of different shapes. This collection of examples provides various representations of regular pentagons, emphasizing the importance of side length equality in classification. |
Definition of a Polygon |
|
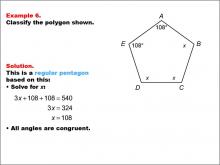
Math Example--Polygons--Polygon Classification: Example 6 | Math Example--Polygons--Polygon Classification: Example 6TopicPolygons DescriptionThis example features a pentagon labeled with vertices A, B, C, D, and E, where two angles are marked as 108 degrees, and the other angles are marked as "x". It demonstrates how to determine if a pentagon is regular by solving for the unknown angle measures. Understanding polygon classification is essential in geometry as it helps students analyze and categorize shapes based on their properties. This collection of examples highlights different aspects of regular pentagons, emphasizing both side length and angle measure as defining characteristics. |
Definition of a Polygon |
|
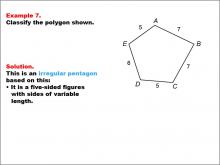
Math Example--Polygons--Polygon Classification: Example 7 | Math Example--Polygons--Polygon Classification: Example 7TopicPolygons DescriptionThis example showcases a pentagon labeled with vertices A, B, C, D, and E, where the sides have different lengths: 5, 7, 7, 5, and 6 units. It illustrates an irregular pentagon, demonstrating that not all five-sided figures are regular. Polygon classification is a crucial topic in geometry that helps students distinguish between regular and irregular shapes. This collection of examples provides a comprehensive look at various types of pentagons, highlighting the differences between regular and irregular polygons based on side lengths and angle measures. |
Definition of a Polygon |
|
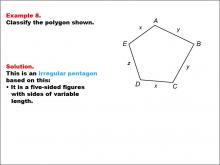
Math Example--Polygons--Polygon Classification: Example 8 | Math Example--Polygons--Polygon Classification: Example 8TopicPolygons DescriptionThis example presents a pentagon labeled with vertices A, B, C, D, and E, where the sides are marked with variables x, y, and z, indicating different lengths. It demonstrates another instance of an irregular pentagon, emphasizing that side length variation results in irregularity. Understanding polygon classification is crucial in geometry as it helps students recognize and categorize shapes based on their properties. This collection of examples highlights the differences between regular and irregular pentagons, focusing on side length as a key determining factor. |
Definition of a Polygon |
|
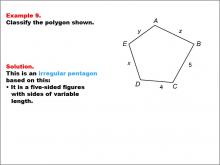
Math Example--Polygons--Polygon Classification: Example 9 | Math Example--Polygons--Polygon Classification: Example 9TopicPolygons DescriptionThis example features a pentagon labeled with vertices A, B, C, D, E, where the sides are labeled as y, z, 5, 4, and x. It illustrates another case of an irregular pentagon, demonstrating that the presence of different side lengths, including both numeric and variable representations, results in irregularity. Polygon classification is a fundamental concept in geometry that helps students analyze and categorize shapes based on their properties. This collection of examples provides a comprehensive look at various types of pentagons, emphasizing the importance of side length equality in determining regularity. |
Definition of a Polygon |

|
Math Example--Polygons--Quadrilateral Classification: Example 1 | Math Example--Polygons--Quadrilateral Classification: Example 1TopicGeometry DescriptionThis example presents a quadrilateral with labeled sides: AB = 5, BC = 4, CD = 3, and DA = 6. The task is to classify the quadrilateral based on these measurements. Since none of the sides are congruent and no specific relationships among the sides can be determined, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 10 | Math Example--Polygons--Quadrilateral Classification: Example 10TopicGeometry DescriptionThis example showcases a quadrilateral with right angles labeled with variable x at two corners, labeled as A, B, C, and D. To classify this shape, we need to solve for x: 90 + 90 + 2x = 360, which gives us x = 90. This means all angles are 90 degrees. Since opposite sides are parallel and congruent, we can classify this shape as a rectangle. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 11 | Math Example--Polygons--Quadrilateral Classification: Example 11TopicGeometry DescriptionThis example presents a square with all sides congruent and right angles, labeled as A, B, C, and D. The task is to classify the quadrilateral based on these characteristics. As all interior angles are 90 degrees and all sides are congruent, this shape is confirmed to be a square. |
Definition of a Quadrilateral |
|
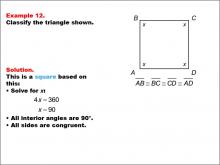
Math Example--Polygons--Quadrilateral Classification: Example 12 | Math Example--Polygons--Quadrilateral Classification: Example 12TopicGeometry DescriptionThis example features a quadrilateral with all sides labeled x and marked congruent, labeled as A, B, C, and D. To classify this shape, we need to solve for x: 4x = 360, which gives us x = 90. This means all angles are 90 degrees. Since all sides are congruent and all angles are right angles, we can classify this shape as a square. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 13 | Math Example--Polygons--Quadrilateral Classification: Example 13TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. The side lengths are indicated with x. To classify this shape, we solve for x: 90 + 90 + 2x = 360, which gives us x = 90. This confirms that all interior angles are 90 degrees. Since all sides are congruent and all angles are right angles, we can classify this shape as a square. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 14 | Math Example--Polygons--Quadrilateral Classification: Example 14TopicGeometry DescriptionThis example showcases a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. Each side is labeled with a length of 1. Based on these characteristics, we can classify this shape as a square. All sides are congruent, which means opposite sides are parallel. Angle ABC is 90 degrees, and its adjacent angles are supplementary, confirming that all interior angles are 90 degrees. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 15 | Math Example--Polygons--Quadrilateral Classification: Example 15TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. The side lengths are indicated with x. Based on these characteristics, we can classify this shape as a square. Because all sides are congruent, opposite sides are parallel. Angle ABC is 90 degrees, and its adjacent angles are supplementary, confirming that all interior angles are 90 degrees. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 16 | Math Example--Polygons--Quadrilateral Classification: Example 16TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with two sides labeled with lengths of 5 and x, and angles marked as right angles. The diagram shows perpendicular lines and parallel lines. Based on these characteristics, we can classify this shape as a square. Because angle ABC and angle BAD are supplementary, BC and AD are parallel. Since AB and CD are congruent, angle BAD and angle ADC are supplementary. Therefore, all interior angles are 90 degrees, and all sides are congruent. |
Definition of a Quadrilateral |
|
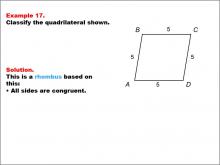
Math Example--Polygons--Quadrilateral Classification: Example 17 | Math Example--Polygons--Quadrilateral Classification: Example 17TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with all sides marked as 5 units, indicating congruence. Based on this characteristic, we can classify this shape as a rhombus. The key property that defines a rhombus is that all sides are congruent, which is clearly demonstrated in this example. |
Definition of a Quadrilateral |
|
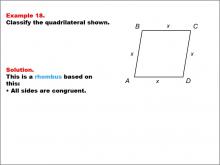
Math Example--Polygons--Quadrilateral Classification: Example 18 | Math Example--Polygons--Quadrilateral Classification: Example 18TopicGeometry DescriptionThis example showcases a quadrilateral labeled ABCD with all sides marked as x, indicating congruence. Based on this characteristic, we can classify this shape as a rhombus. The defining property of a rhombus is that all sides are congruent, which is clearly demonstrated in this example by using the variable x for all side lengths. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 19 | Math Example--Polygons--Quadrilateral Classification: Example 19TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides AB and CD marked as x, and BC and AD marked as 5. Opposite sides are noted to be parallel. Based on these characteristics, we can classify this shape as a rhombus. The key properties that define this as a rhombus are: opposite sides are parallel, and opposite sides are congruent. Since x = 5, all sides are congruent, which is a defining property of a rhombus. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 2 | Math Example--Polygons--Quadrilateral Classification: Example 2TopicGeometry DescriptionThis example showcases a quadrilateral with sides labeled as variables: x, y, z, and w. The task is to classify the quadrilateral based on this information. As no specific relationships between the sides are given, and no sides are stated to be congruent, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |
|
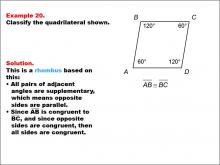
Math Example--Polygons--Quadrilateral Classification: Example 20 | Math Example--Polygons--Quadrilateral Classification: Example 20TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with angles B and D marked as 120 degrees, and angles A and C as 60 degrees. Sides AB and BC are marked as congruent. Based on these characteristics, we can classify this shape as a rhombus. All pairs of adjacent angles are supplementary (120° + 60° = 180°), which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent in a parallelogram, all sides must be congruent, defining this shape as a rhombus. |
Definition of a Quadrilateral |
|
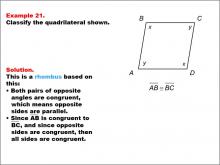
Math Example--Polygons--Quadrilateral Classification: Example 21 | Math Example--Polygons--Quadrilateral Classification: Example 21TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides marked as x and y. The opposite sides are noted to be congruent, and there's an additional note indicating AB is congruent to BC. Based on these characteristics, we can classify this shape as a rhombus. Both pairs of opposite angles are congruent, which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent, all sides must be congruent, defining this shape as a rhombus. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 22 | Math Example--Polygons--Quadrilateral Classification: Example 22TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with angles marked as 70° and sides marked as x. Opposite angles are noted to be congruent, and there's an additional note indicating AB is congruent to BC. Based on these characteristics, we can classify this shape as a rhombus. Both pairs of opposite angles are congruent, which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent in a parallelogram, all sides must be congruent, defining this shape as a rhombus. |
Definition of a Quadrilateral |
|
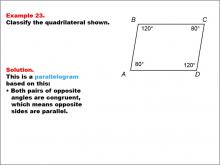
Math Example--Polygons--Quadrilateral Classification: Example 23 | Math Example--Polygons--Quadrilateral Classification: Example 23TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with angles marked as 120° and 80°. Opposite angles are noted to be congruent. Based on these characteristics, we can classify this shape as a parallelogram. Both pairs of opposite angles are congruent, which means opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |
|
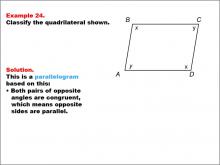
Math Example--Polygons--Quadrilateral Classification: Example 24 | Math Example--Polygons--Quadrilateral Classification: Example 24TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides marked as x and y. The opposite sides are noted to be congruent. Based on these characteristics, we can classify this shape as a parallelogram. Both pairs of opposite sides are congruent, which means opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |
|
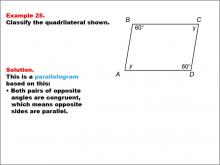
Math Example--Polygons--Quadrilateral Classification: Example 25 | Math Example--Polygons--Quadrilateral Classification: Example 25TopicGeometry DescriptionThis example showcases a quadrilateral labeled ABCD with angles at B and D marked as 60 degrees. Sides AD and BC are labeled y. The shape is identified as a parallelogram. This classification is based on the fact that both pairs of opposite angles are congruent, which means opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |
|
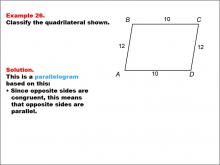
Math Example--Polygons--Quadrilateral Classification: Example 26 | Math Example--Polygons--Quadrilateral Classification: Example 26TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides AB and CD measuring 10, and sides BC and AD measuring 12. The shape is identified as a parallelogram. This classification is based on the fact that opposite sides are congruent, which means that opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |
|
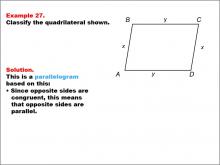
Math Example--Polygons--Quadrilateral Classification: Example 27 | Math Example--Polygons--Quadrilateral Classification: Example 27TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with sides AB and CD labeled y, and sides AD and BC labeled x. The shape is identified as a parallelogram. This classification is based on the fact that opposite sides are congruent, which means that opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 28 | Math Example--Polygons--Quadrilateral Classification: Example 28TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides BC and AD parallel, and AB and CD parallel. Side BC is marked as 5, and side AD is marked as x. Based on these characteristics, we can classify this shape as a parallelogram. Opposite sides are parallel (BC // AD, AB // CD), which is the defining property of a parallelogram. However, adjacent sides are not necessarily congruent, as BC is 5 and AD is x. |
Definition of a Quadrilateral |
|
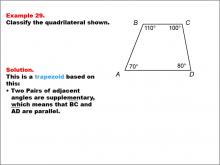
Math Example--Polygons--Quadrilateral Classification: Example 29 | Math Example--Polygons--Quadrilateral Classification: Example 29TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with angles marked as 110°, 100°, 70°, and 80°. Two pairs of adjacent angles are supplementary. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel. |
Definition of a Quadrilateral |
|
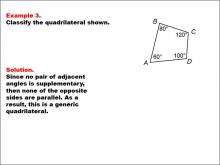
Math Example--Polygons--Quadrilateral Classification: Example 3 | Math Example--Polygons--Quadrilateral Classification: Example 3TopicGeometry DescriptionThis example presents a quadrilateral with labeled angles: A = 60°, B = 80°, C = 120°, and D = 100°. The task is to classify the quadrilateral based on these angle measurements. Since no pair of adjacent angles is supplementary (adds up to 180°), none of the opposite sides are parallel. As a result, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |
|
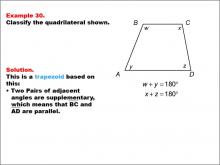
Math Example--Polygons--Quadrilateral Classification: Example 30 | Math Example--Polygons--Quadrilateral Classification: Example 30TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with angles marked as w, x, y, and z. It states that w + y = 180° and x + z = 180°. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel. |
Definition of a Quadrilateral |
|
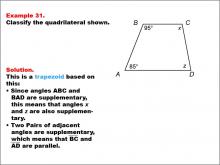
Math Example--Polygons--Quadrilateral Classification: Example 31 | Math Example--Polygons--Quadrilateral Classification: Example 31TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with angles ABC = 95° and BAD = 85°. It states that angles x and z are also supplementary due to two pairs of adjacent angles being supplementary. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel. |
Definition of a Quadrilateral |
|
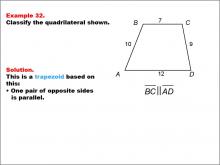
Math Example--Polygons--Quadrilateral Classification: Example 32 | Math Example--Polygons--Quadrilateral Classification: Example 32TopicGeometry DescriptionThis example showcases a trapezoid with vertices labeled A, B, C, D. The side lengths are given as AB = 10, BC = 7, CD = 9, and AD = 12. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel. |
Definition of a Quadrilateral |
|
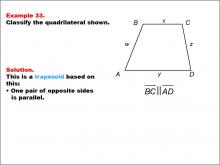
Math Example--Polygons--Quadrilateral Classification: Example 33 | Math Example--Polygons--Quadrilateral Classification: Example 33TopicGeometry DescriptionThis example presents a trapezoid with vertices labeled A, B, C, D. The sides are labeled as w, x, y, and z. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel. |
Definition of a Quadrilateral |
|
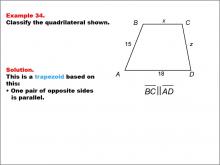
Math Example--Polygons--Quadrilateral Classification: Example 34 | Math Example--Polygons--Quadrilateral Classification: Example 34TopicGeometry DescriptionThis example features a trapezoid with vertices labeled A, B, C, D. The side lengths are given as AB = 15, BC = x, CD = z, and AD = 18. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 4 | Math Example--Polygons--Quadrilateral Classification: Example 4TopicGeometry DescriptionThis example features a quadrilateral with angles labeled as variables: x, y, z, and w. The task is to classify the quadrilateral based on this information. As no specific relationships between the angles are given, and no angles are stated to be congruent or supplementary, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 5 | Math Example--Polygons--Quadrilateral Classification: Example 5TopicGeometry DescriptionThis example presents a quadrilateral with no right angles or congruent sides, labeled with angles and side lengths. The task is to classify the quadrilateral based on these characteristics. Since no adjacent angles are supplementary and no sides are parallel, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 6 | Math Example--Polygons--Quadrilateral Classification: Example 6TopicGeometry DescriptionThis example showcases a rectangle with opposite sides labeled as 3 and 1, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. As the shape has opposite sides that are congruent and all interior angles are 90 degrees, it is identified as a rectangle. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 7 | Math Example--Polygons--Quadrilateral Classification: Example 7TopicGeometry DescriptionThis example presents a rectangle with opposite sides labeled x and y, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. Due to the congruent opposite sides and all interior angles being 90 degrees, this shape is identified as a rectangle. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 8 | Math Example--Polygons--Quadrilateral Classification: Example 8TopicGeometry DescriptionThis example features a rectangle with sides labeled 7 and 5, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. As all interior angles are 90 degrees and opposite sides are parallel and congruent, this shape is confirmed to be a rectangle. |
Definition of a Quadrilateral |