
Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 2: Adjacent Angles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Example--Area and Perimeter--Quadrilaterals: Example 16 | Math Example--Area and Perimeter--Quadrilaterals: Example 16TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's perimeter using algebraic expressions. The rectangle ABCD has a length of x + 25 units and a width of x - 7 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2[(x + 25) + (x - 7)] = 2(2x + 18) = 4x + 36 units. |
Area and Perimeter of Quadrilaterals |
|
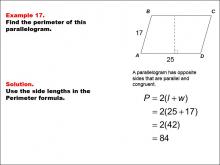
Math Example--Area and Perimeter--Quadrilaterals: Example 17 | Math Example--Area and Perimeter--Quadrilaterals: Example 17TopicGeometry DescriptionThis example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units. |
Area and Perimeter of Quadrilaterals |
|
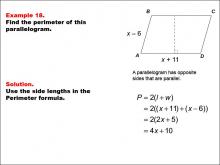
Math Example--Area and Perimeter--Quadrilaterals: Example 18 | Math Example--Area and Perimeter--Quadrilaterals: Example 18TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 19 | Math Example--Area and Perimeter--Quadrilaterals: Example 19TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 2 | Math Example--Area and Perimeter--Quadrilaterals: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units. Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 20 | Math Example--Area and Perimeter--Quadrilaterals: Example 20TopicGeometry DescriptionThis example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 21 | Math Example--Area and Perimeter--Quadrilaterals: Example 21TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 22 | Math Example--Area and Perimeter--Quadrilaterals: Example 22TopicGeometry DescriptionThis example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 23 | Math Example--Area and Perimeter--Quadrilaterals: Example 23TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a kite. The kite ABCD has two pairs of equal sides: AB and AD measure 22 units each, while BC and CD measure 11 units each. To find the perimeter, we add all four side lengths. In this case, P = 22 + 22 + 11 + 11 = 66 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 24 | Math Example--Area and Perimeter--Quadrilaterals: Example 24TopicGeometry DescriptionThis example illustrates the calculation of a kite's perimeter using algebraic expressions. The kite ABCD has two pairs of equal sides: AB and AD measure x + 11 units each, while BC and CD measure x - 5 units each. To find the perimeter, we add all four side lengths. In this case, P = (x + 11) + (x + 11) + (x - 5) + (x - 5) = 4x + 12 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 3 | Math Example--Area and Perimeter--Quadrilaterals: Example 3TopicGeometry DescriptionThis example demonstrates how to calculate the area of a rectangle. The rectangle ABCD has a length of 12 units and a width of 8 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = 12 × 8 = 96 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 4 | Math Example--Area and Perimeter--Quadrilaterals: Example 4TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's area using algebraic expressions. The rectangle ABCD has a length of x + 10 units and a width of x - 3 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = (x + 10)(x - 3) = x² + 7x - 30 square units. |
Area and Perimeter of Quadrilaterals |
|
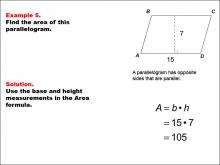
Math Example--Area and Perimeter--Quadrilaterals: Example 5 | Math Example--Area and Perimeter--Quadrilaterals: Example 5TopicGeometry DescriptionThis example illustrates how to calculate the area of a parallelogram. The parallelogram ABCD has a base of 15 units and a height of 7 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 15 × 7 = 105 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 6 | Math Example--Area and Perimeter--Quadrilaterals: Example 6TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's area using algebraic expressions. The parallelogram ABCD has a base of x + 9 units and a height of x - 4 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 9)(x - 4) = x² + 5x - 36 square units. |
Area and Perimeter of Quadrilaterals |
|
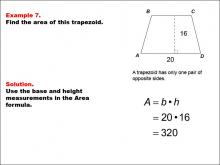
Math Example--Area and Perimeter--Quadrilaterals: Example 7 | Math Example--Area and Perimeter--Quadrilaterals: Example 7TopicGeometry DescriptionThis example illustrates how to calculate the area of a trapezoid. The trapezoid ABCD has a base of 20 units and a height of 16 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 20 × 16 = 320 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 8 | Math Example--Area and Perimeter--Quadrilaterals: Example 8TopicGeometry DescriptionThis example demonstrates the calculation of a trapezoid's area using algebraic expressions. The trapezoid ABCD has a base of x + 12 units and a height of x - 5 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 12)(x - 5) = x² + 7x - 60 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 9 | Math Example--Area and Perimeter--Quadrilaterals: Example 9TopicGeometry DescriptionThis example illustrates how to calculate the area of a rhombus. The rhombus ABCD has a side length of 25 units and a height (perpendicular distance between parallel sides) of 19 units. To find the area, we use the formula A = b × h, where b is the base (which is the same as the side length in a rhombus) and h is the height. In this case, A = 25 × 19 = 475 square units. |
Area and Perimeter of Quadrilaterals |
|
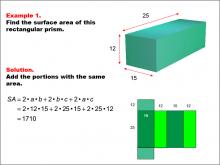
Math Example--Area and Perimeter--Surface Area: Example 1 | Math Example--Area and Perimeter--Surface Area: Example 1TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular prism. The prism has dimensions of 25, 15, and 12 units. The surface area is determined by summing the areas of all faces, which is represented by the formula SA = 2ab + 2bc + 2ac. For this specific prism, the calculation yields a surface area of 1710 square units. |
Surface Area |
|
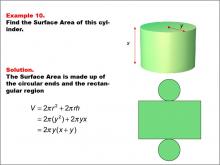
Math Example--Area and Perimeter--Surface Area: Example 10 | Math Example--Area and Perimeter--Surface Area: Example 10TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cylinder with radius y and height x. The surface area consists of two circular ends and the rectangular region forming the curved surface. The formula used is SA = 2πr2 + 2πrh, which simplifies to SA = 2πy(x + y), where y is the radius and x is the height of the cylinder. |
Surface Area |
|
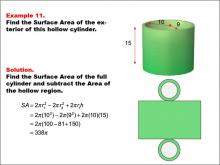
Math Example--Area and Perimeter--Surface Area: Example 11 | Math Example--Area and Perimeter--Surface Area: Example 11TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The surface area is determined by subtracting the area of the hollow region from the full cylinder's surface area. The formula used is SA = 2πr12 - 2πr22 + 2πr1h, where r1 is the outer radius and r2 is the inner radius. For this specific hollow cylinder, the calculation yields a surface area of 338π square units. |
Surface Area |
|
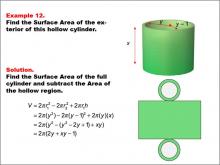
Math Example--Area and Perimeter--Surface Area: Example 12 | Math Example--Area and Perimeter--Surface Area: Example 12TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow cylinder with an outer radius y, an inner radius y - 1, and a height x. The surface area is determined by subtracting the hollow region's area from the full cylinder's surface area. The formula used is SA = 2πr12 - 2πr22 + 2πr1h, which simplifies to SA = 2π(2y + xy - 1), where r1 is the outer radius (y) and r2 is the inner radius (y - 1). |
Surface Area |
|
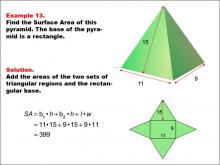
Math Example--Area and Perimeter--Surface Area: Example 13 | Math Example--Area and Perimeter--Surface Area: Example 13TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular-based pyramid with dimensions 11, 9, and 15 units. The pyramid is depicted with its net unfolded, showing two triangular faces and a rectangular base. The surface area is calculated using the formula SA = b1 * h + b2 * h + l * w, where b1 and b2 are the bases of the triangular faces, h is the height of the triangular faces, and l and w are the length and width of the rectangular base. For this specific pyramid, the calculation yields a surface area of 399 square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 14 | Math Example--Area and Perimeter--Surface Area: Example 14TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a rectangular-based pyramid with dimensions labeled as x, y, and z. The pyramid is depicted with its net unfolded into two triangular faces and one rectangular base. The surface area is calculated using the formula SA = b1 * h + b2 * h + l * w, which simplifies to SA = xz + yz + xy, where x and y are the dimensions of the rectangular base, and z is the height of the triangular faces. |
Surface Area |
|
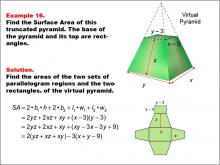
Math Example--Area and Perimeter--Surface Area: Example 15 | Math Example--Area and Perimeter--Surface Area: Example 15TopicSurface Area |
Surface Area |
|
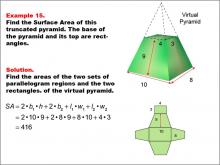
Math Example--Area and Perimeter--Surface Area: Example 16 | Math Example--Area and Perimeter--Surface Area: Example 16TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a truncated rectangular-based pyramid with dimensions labeled as x - 3, y - 3, z, x, and y. The virtual pyramid is shown with its net unfolded into four parallelogram regions and two rectangles. The surface area is calculated using the formula SA = 2yz + 2xz + xy + (x - 3)(y - 3), which simplifies to SA = (yz + xz + xy) - (x + y - 9). |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 17 | Math Example--Area and Perimeter--Surface Area: Example 17TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a sphere with a radius of 3 units. The surface area is calculated using the formula SA = 4πr2, where r is the radius of the sphere. For this specific sphere, the calculation yields a surface area of 36π square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 18 | Math Example--Area and Perimeter--Surface Area: Example 18TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a sphere with an unknown radius labeled as "x". The surface area is calculated using the formula SA = 4πr2, which in this case becomes SA = 4πx2, where x is the radius of the sphere. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 19 | Math Example--Area and Perimeter--Surface Area: Example 19TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cube with a side length of 7 units. The surface area is calculated using the formula SA = 6s2, where s is the length of one side of the cube. For this specific cube, the calculation yields a surface area of 294 square units. |
Surface Area |
|
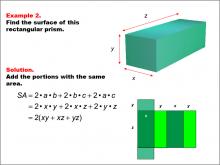
Math Example--Area and Perimeter--Surface Area: Example 2 | Math Example--Area and Perimeter--Surface Area: Example 2TopicSurface Area DescriptionThis example introduces a general formula for calculating the surface area of a rectangular prism with dimensions x, y, and z. The surface area is computed using the formula SA = 2xy + 2xz + 2yz, which can be simplified to 2(xy + xz + yz). This generalized approach allows for easy application to prisms of various sizes. Surface area calculations are fundamental in mathematics, with applications ranging from manufacturing to environmental science. This collection of examples aids in teaching the topic by presenting both specific and general cases, helping students understand how to apply formulas flexibly to different scenarios. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 20 | Math Example--Area and Perimeter--Surface Area: Example 20TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cube with an unknown side length labeled as "x". The surface area is calculated using the formula SA = 6s2, which in this case becomes SA = 6x2, where x is the length of one side of the cube. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 21 | Math Example--Area and Perimeter--Surface Area: Example 21TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow cube with an outer side length of 9 units and an inner hollow square side length of 7 units. The surface area is calculated using the formula SA = 6 * s12 - 2 * s22, where s1 is the outer side length and s2 is the inner side length. For this specific hollow cube, the calculation yields a surface area of 388 square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 22 | Math Example--Area and Perimeter--Surface Area: Example 22TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow cube with variable dimensions. The outer side length is labeled as "x" and the inner hollow side length as "x - 2". The surface area is calculated using the formula SA = 6 * s12 - 2 * s22, where s1 = x and s2 = x - 2. After expanding and simplifying, the result is SA = 4(x2 + 2x - 2) square units. |
Surface Area |
|
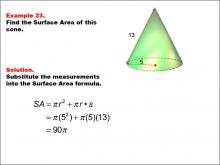
Math Example--Area and Perimeter--Surface Area: Example 23 | Math Example--Area and Perimeter--Surface Area: Example 23TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cone with a radius of 5 units and a slant height of 13 units. The surface area is calculated using the formula SA = π * r2 + π * r * s, where r is the radius and s is the slant height. For this specific cone, the calculation yields a surface area of 90π square units. |
Surface Area |

|
Math Example--Area and Perimeter--Surface Area: Example 24 | Math Example--Area and Perimeter--Surface Area: Example 24TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a cone with variable dimensions. The radius is labeled as "x" and the slant height as "y". The surface area is calculated using the formula SA = π * r2 + π * r * s, where r = x and s = y. This simplifies to SA = π * x(x + y) square units. |
Surface Area |
|
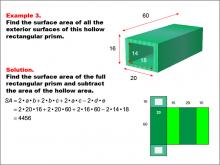
Math Example--Area and Perimeter--Surface Area: Example 3 | Math Example--Area and Perimeter--Surface Area: Example 3TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow rectangular prism. The outer dimensions are 60, 20, and 16 units, while the inner dimensions are 18 and 14 units. The surface area is determined by subtracting the area of the hollow region from the surface area of the full rectangular prism, resulting in a surface area of 4456 square units. |
Surface Area |
|
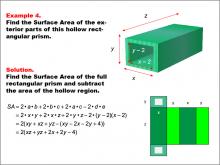
Math Example--Area and Perimeter--Surface Area: Example 4 | Math Example--Area and Perimeter--Surface Area: Example 4TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow rectangular prism. The outer dimensions are represented by x, y, and z, while the hollow dimensions are represented by (y - 2) and (x - 2). The surface area is determined by subtracting the hollow region's surface area from that of the full rectangular prism, resulting in the formula SA = 2(xz + yz + 2x + 2y - 4). |
Surface Area |
|
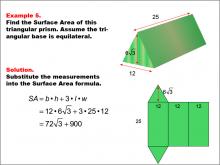
Math Example--Area and Perimeter--Surface Area: Example 5 | Math Example--Area and Perimeter--Surface Area: Example 5TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a triangular prism with an equilateral triangular base. The base is 12 units, the height is 6 * √(3), and the length of the prism is 25 units. The surface area is calculated using the formula SA = b * h + 3 * l * w, where b is the base, h is the height of the triangle, l is the length of the prism, and w is the width of the triangle. The final result is 72 * √(3) + 900 square units. |
Surface Area |
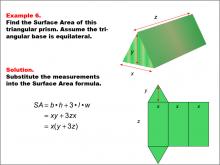
|
Math Example--Area and Perimeter--Surface Area: Example 6 | Math Example--Area and Perimeter--Surface Area: Example 6TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a triangular prism with an equilateral triangular base. The dimensions are represented by x for the base, y for the height of the triangle, and z for the length of the prism. The surface area is determined using the formula SA = b * h + 3 * l * w, which simplifies to SA = xy + 3zx = x(y + 3z). |
Surface Area |
|
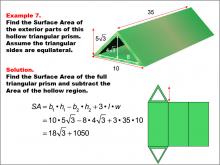
Math Example--Area and Perimeter--Surface Area: Example 7 | Math Example--Area and Perimeter--Surface Area: Example 7TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a hollow triangular prism with an equilateral triangular base. The outer triangle has a base of 10 units and a height of 5 * √(3), while the inner triangle has a base of 8 units and a height of 4 * √(3). The length of the prism is 35 units. The surface area is calculated by subtracting the area of the hollow region from the full prism's surface area, resulting in SA = b1 * h1 - b2 * h2 + 3 * l * w = (18 * √(3)) + 1050 square units. |
Surface Area |
|
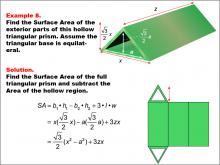
Math Example--Area and Perimeter--Surface Area: Example 8 | Math Example--Area and Perimeter--Surface Area: Example 8TopicSurface Area DescriptionThis example presents a general formula for calculating the surface area of a hollow triangular prism with an equilateral triangular base. The outer triangle has a base labeled as x, and the inner triangle has a base labeled as a. The heights are given as √(3)/2 for both triangles, and the length of the prism is z units. The surface area is determined by subtracting the area of the hollow region from the full prism's surface area, resulting in the formula SA = (√(3)/2) (x2 - a2) + 3zx. |
Surface Area |
|
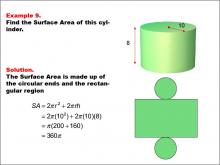
Math Example--Area and Perimeter--Surface Area: Example 9 | Math Example--Area and Perimeter--Surface Area: Example 9TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a cylinder with a radius of 10 units and a height of 8 units. The surface area consists of two circular ends and the rectangular region forming the curved surface. The formula used is SA = 2πr2 + 2πrh, where r is the radius and h is the height. For this specific cylinder, the calculation yields a surface area of 360π square units. |
Surface Area |

|
Math Example--Area and Perimeter--Triangles: Example 1 | Math Example--Area and Perimeter--Triangles: Example 1TopicGeometry DescriptionThis example demonstrates how to calculate the area of a scalene triangle. The triangle has sides measuring 5, 7, and 9 units, with a height of 3 units from the base of 7. To find the area, we use the formula A = 1/2 * b * h. In this case, A = 1/2 * 7 * 3 = 10.5 square units. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 10 | Math Example--Area and Perimeter--Triangles: Example 10TopicGeometry DescriptionThis example explores the area calculation of an equilateral triangle using algebraic expressions. The triangle has all sides labeled as x, with the height expressed as (√3/2) * x. Students are guided through the process of deriving and applying the area formula for this general case of an equilateral triangle. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 11 | Math Example--Area and Perimeter--Triangles: Example 11TopicGeometry DescriptionThis example demonstrates the calculation of area for a right triangle with specific dimensions. The triangle has legs measuring 8 and 15 units. Students are guided through the process of applying the area formula to this straightforward case. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 12 | Math Example--Area and Perimeter--Triangles: Example 12TopicGeometry DescriptionThis example introduces algebraic expressions in the context of right triangle area calculations. The triangle's legs are labeled x and y, challenging students to express the area formula using these variables. Integrating algebra into geometric problems is a key skill in advanced mathematics. This collection of examples helps teach this topic by demonstrating how algebraic expressions can represent right triangle dimensions. Students learn to manipulate these expressions within the area formula, deepening their understanding of both algebra and geometry. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 13 | Math Example--Area and Perimeter--Triangles: Example 13TopicGeometry DescriptionThis example focuses on calculating the area of an isosceles right triangle. The triangle has two equal legs measuring 13 units each, with angles of 45 degrees. Students are guided through applying the area formula to this specific case, which combines properties of both isosceles and right triangles. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 14 | Math Example--Area and Perimeter--Triangles: Example 14TopicGeometry DescriptionThis example combines the concepts of isosceles right triangles and algebraic expressions. The triangle has two equal legs labeled as x, with angles of 45 degrees. Students are challenged to express the area formula using this variable, applying their knowledge of both triangle properties and algebraic manipulation. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 15 | Math Example--Area and Perimeter--Triangles: Example 15TopicGeometry DescriptionThis example focuses on calculating the area of a 30-60-90 right triangle. The triangle has a base of 16 units and a height of 8√3 units. Students are guided through applying the area formula to this specific case, which involves working with irrational numbers. |
Area and Perimeter of Triangles |

|
Math Example--Area and Perimeter--Triangles: Example 16 | Math Example--Area and Perimeter--Triangles: Example 16TopicGeometry DescriptionThis example combines the properties of 30-60-90 right triangles with algebraic expressions. The triangle has a base of x + 5 and a height of (x + 5)/2 * √3. Students are challenged to express the area formula using these algebraic terms, applying their knowledge of both special right triangles and algebraic manipulation. |
Area and Perimeter of Triangles |
|
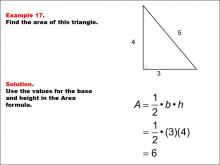
Math Example--Area and Perimeter--Triangles: Example 17 | Math Example--Area and Perimeter--Triangles: Example 17TopicGeometry DescriptionThis example focuses on calculating the area of a 3-4-5 right triangle. This triangle is a special case of right triangles with integer side lengths. Students are guided through applying the area formula to this specific case, which is straightforward due to its simple dimensions. |
Area and Perimeter of Triangles |