
Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 2: Adjacent Angles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Lesson Plan: Cross-Sections of 3D Figures, Part 3 | Lesson Plan: Cross-Sections of Triangular Prisms, Antiprisms, and Tetrahedrons In this engaging geometry lesson, students will explore cross-sections of triangular prisms, antiprisms, and tetrahedrons. Through hands-on activities, real-world examples, and animated visuals, students will investigate how different slicing planes impact three-dimensional figures. By analyzing horizontal, vertical, and diagonal cross-sections, students will develop a deeper understanding of geometric properties and spatial reasoning. |
Applications of 3D Geometry |

|
Lesson Plan: Nets of 3D Figures, Part 1 | Lesson Plan: Introduction to Nets and Basic 3D Shapes In this engaging and interactive lesson, students explore the connection between 2D nets and 3D geometric figures. Through animations, printable foldable nets, and hands-on activities, students will develop a deeper understanding of how nets transform into solid figures such as cubes, rectangular prisms, and triangular prisms. This lesson also reinforces key geometry concepts, including faces, edges, and vertices, while guiding students through surface area calculations using nets. |
3-Dimensional Figures |

|
Lesson Plan: Nets of 3D Figures, Part 2 | Lesson Plan: Pyramids, Tetrahedra, and Octahedra In this engaging lesson, students explore the geometry of pyramids, tetrahedra, and octahedra using 2D nets and 3D models. Through interactive animations, printable foldable nets, and hands-on activities, students develop a deeper understanding of how pyramids differ from prisms and why their triangular faces provide structural stability. This lesson covers key geometry concepts, including faces, edges, vertices, and surface area calculations. |
3-Dimensional Figures |

|
Lesson Plan: Nets of 3D Figures, Part 3 | Lesson Plan: Advanced Polyhedra and Cylindrical Shapes In this interactive lesson, students explore the geometry of cylinders and advanced polyhedra, including the dodecahedron and icosahedron. Using 2D nets and 3D models, students will construct these shapes, analyze their faces, edges, and vertices, and compare their properties to simpler geometric figures. This lesson emphasizes the differences between curved-surface shapes, like cylinders, and flat-faced polyhedra. |
3-Dimensional Figures |
|
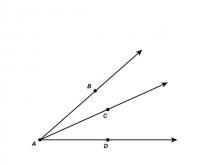
Math Clip Art--Angle Illustrations--Adjacent Angles--Labeled | Math Clip Art--Angle Illustrations--Adjacent Angles--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
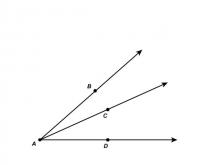
Math Clip Art--Angle Illustrations--Adjacent Angles--Unlabeled | Math Clip Art--Angle Illustrations--Adjacent Angles--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
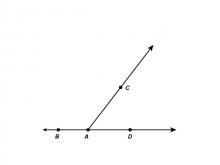
Math Clip Art--Angle Illustrations--Supplementary Angles--Labeled | Math Clip Art--Angle Illustrations--Supplementary Angles--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
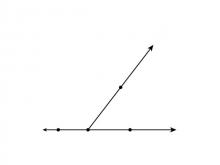
Math Clip Art--Angle Illustrations--Supplementary Angles--Unlabeled | Math Clip Art--Angle Illustrations--Supplementary Angles--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
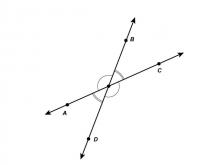
Math Clip Art--Angle Illustrations--Vertical Angles--Labeled | Math Clip Art--Angle Illustrations--Vertical Angles--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
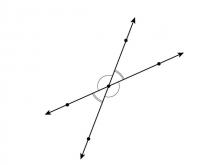
Math Clip Art--Angle Illustrations--Vertical Angles--Unlabeled | Math Clip Art--Angle Illustrations--Vertical Angles--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
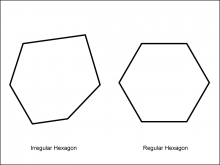
Math Clip Art--Geometry Concepts--Polygons--Hexagon | Math Clip Art--Polygons--HexagonTopicGeometry Concepts DescriptionThis image illustrates two hexagons: one regular and one irregular. A hexagon is a six-sided polygon. In a regular hexagon, all sides and angles are equal, with each interior angle measuring 120 degrees. This symmetry gives it a balanced and uniform appearance. An irregular hexagon, by contrast, has sides and angles that are not all equal. This lack of uniformity means that the hexagon can take on a variety of shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
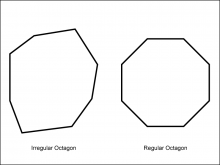
Math Clip Art--Geometry Concepts--Polygons--Octagon | Math Clip Art--Polygons--OctagonTopicGeometry Concepts DescriptionThis image shows two octagons: one regular and one irregular. An octagon is an eight-sided polygon. In a regular octagon, all sides and angles are equal, with each interior angle measuring 135 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular octagon, on the other hand, has sides and angles that are not all equal. This asymmetry means that the octagon can have a variety of shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
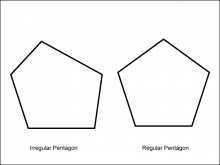
Math Clip Art--Geometry Concepts--Polygons--Pentagon | Math Clip Art--Polygons--PentagonTopicGeometry Concepts DescriptionThis image depicts two pentagons: one regular and one irregular. A pentagon is a five-sided polygon. In a regular pentagon, all sides and angles are equal, with each interior angle measuring 108 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular pentagon, however, has sides and angles that are not all equal. This asymmetry allows the pentagon to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
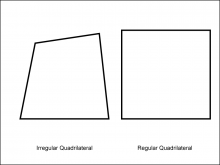
Math Clip Art--Geometry Concepts--Polygons--Quadrilateral | Math Clip Art--Polygons--QuadrilateralTopicGeometry Concepts DescriptionThis image illustrates two quadrilaterals: one regular and one irregular. A quadrilateral is a four-sided polygon. In a regular quadrilateral, such as a square, all sides and angles are equal, with each interior angle measuring 90 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular quadrilateral, however, has sides and angles that are not all equal. This asymmetry allows the quadrilateral to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
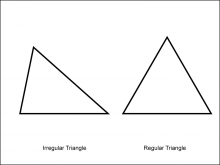
Math Clip Art--Geometry Concepts--Polygons--Triangle | Math Clip Art--Polygons--TriangleTopicGeometry Concepts DescriptionThis image shows two triangles: one regular and one irregular. A triangle is a three-sided polygon. In a regular triangle, also known as an equilateral triangle, all sides and angles are equal, with each interior angle measuring 60 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular triangle, however, has sides and angles that are not all equal. This asymmetry allows the triangle to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
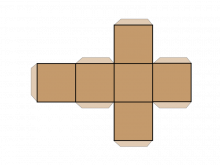
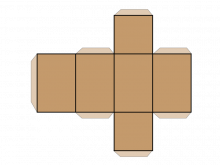
Math Clip Art--Net for a Cube | Math Clip Art--Net for a CubeTopicGeometry DescriptionThis math clip art image is part of a series showcasing 2D nets of 3D figures, specifically focusing on the net for a cube. The image displays a flattened representation of a cube, consisting of six connected squares arranged in a cross-like pattern. This visual aid is crucial for students to understand the relationship between 2D shapes and their 3D counterparts. |
3-Dimensional Figures |
|
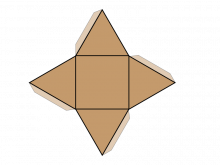
Math Clip Art--Net for a Pyramid | Math Clip Art--Net for a PyramidTopicGeometry DescriptionThis math clip art image is part of a series illustrating 2D nets of 3D figures, with this particular image focusing on the net for a pyramid. The image shows a flattened representation of a square-based pyramid, consisting of a square base surrounded by four triangular faces. This visual aid is essential for students to comprehend how a 3D pyramid can be unfolded into a 2D pattern. |
3-Dimensional Figures |
|
Math Clip Art--Net for a Rectangular Prism | Math Clip Art--Net for a Rectangular PrismTopicGeometry DescriptionThis math clip art image is part of a series showcasing 2D nets of 3D figures, specifically illustrating the net for a rectangular prism. The image displays a flattened representation of a rectangular prism, consisting of six connected rectangles arranged in a cross-like pattern. This visual aid is crucial for students to understand how a 3D rectangular prism can be unfolded into a 2D shape. |
3-Dimensional Figures |
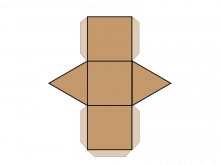
|
Math Clip Art--Net for a Triangular Prism | Math Clip Art--Net for a Triangular PrismTopicGeometry DescriptionThis math clip art image is part of a series illustrating 2D nets of 3D figures, with this particular image focusing on the net for a triangular prism. The image shows a flattened representation of a triangular prism, consisting of two triangular bases and three rectangular faces. This visual aid is essential for students to comprehend how a 3D triangular prism can be unfolded into a 2D pattern. |
3-Dimensional Figures |
|
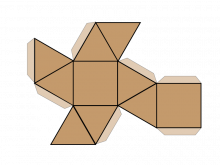
Math Clip Art--Net for an Antiprism | Math Clip Art--Net for an AntiprismTopicGeometry DescriptionThis math clip art image is part of a series showcasing 2D nets of 3D figures, specifically illustrating the net for an antiprism. The image displays a flattened representation of an antiprism, consisting of two polygonal bases (typically regular polygons) connected by a band of triangles. This visual aid is crucial for students to understand how a 3D antiprism can be unfolded into a 2D shape. |
3-Dimensional Figures |
|
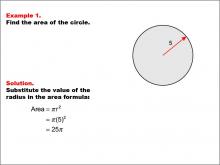
Math Example--Area and Perimeter--Circular Area and Circumference: Example 1 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 1TopicGeometry DescriptionThis example presents a circle with a radius of 5 units. The task is to calculate the area of the circle using the given radius. The solution involves substituting the radius value into the area formula: A = π * r^2 = π * (5)^2 = 25π. Understanding circular area and circumference is integral to mastering geometry. Concepts such as calculating areas and circumferences of circles are fundamental, and exercises like these examples not only provide practice but also deepen the understanding of theoretical concepts in a practical way. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 10TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 11TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π. |
Area and Circumference |
|
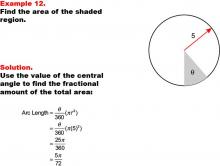
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 12TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 13TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π. |
Area and Circumference |
|
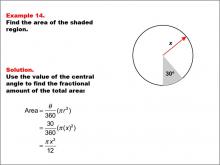
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 14TopicGeometry DescriptionThis example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 15 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 15TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the arc length of the shaded region in terms of x. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * (2 * π * x) = x / 6 * π. |
Area and Circumference |
|
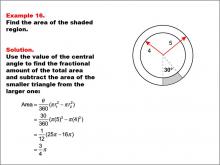
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 16TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4. |
Area and Circumference |
|
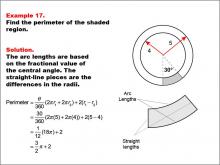
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 17TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 18 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 18TopicGeometry DescriptionThis example features two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x, y, and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * y2) = (θπ / 360) * (x2 - y2). |
Area and Circumference |
|
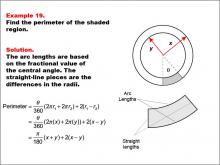
Math Example--Area and Perimeter--Circular Area and Circumference: Example 19 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 19TopicGeometry DescriptionThis example presents two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x, y, and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2πx + 2πy) + 2(x - y) = π/180 * θ(x + y) + 2(x - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 2 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 2TopicGeometry DescriptionThis example features a circle with a radius of 5 units. The objective is to calculate the circumference of the circle using the given radius. The solution involves applying the circumference formula: C = 2 * π * r = 2 * π * (5) = 10π. Circular area and circumference calculations are fundamental in geometry. These examples provide students with practical applications of theoretical concepts, helping them understand the relationship between a circle's radius and its circumference. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 20 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 20TopicGeometry DescriptionThis example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded region in terms of y. The solution involves calculating the difference between the areas of the larger and smaller circles, accounting for the central angle: Area = π/12 * (25 - y2). |
Area and Circumference |
|
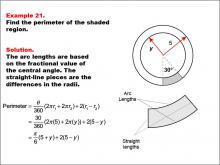
Math Example--Area and Perimeter--Circular Area and Circumference: Example 21 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 21TopicGeometry DescriptionThis example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. Given a central angle of 30 degrees, radius 5, and unknown radius y, the perimeter is calculated as: Perimeter = π/6 * (5 + y) + 2(5 - y). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 22 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 22TopicGeometry DescriptionThis example presents two concentric circles with radii 4 and x, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * 42) = (θ * π / 360) * (x2 - 16). |
Area and Circumference |
|
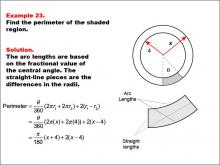
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 23TopicGeometry DescriptionThis example features two concentric circles with radii x and 4, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * x + 2 * π * 4) + 2 * (x - 4) = (π / 180) * θ(x + 4) + 2(x - 4). |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 3 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 3TopicGeometry DescriptionThis example introduces a circle with an unknown radius represented by x. The task is to express the area of the circle in terms of x. The solution demonstrates how to use the area formula with a variable radius: A = π * r2 = π * (x)2 = π * x2. Working with variable expressions in geometry helps students transition from concrete to abstract thinking. This example bridges the gap between numerical calculations and algebraic representations, a crucial skill in advanced mathematics. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 4 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 4TopicGeometry DescriptionThis example presents a circle with an unknown radius represented by x. The task is to express the circumference of the circle in terms of x. The solution demonstrates how to use the circumference formula with a variable radius: C = 2 * π * r = 2 * π * x = 2πx. Understanding circular area and circumference is crucial in geometry. This example helps students transition from concrete numerical values to abstract algebraic expressions, fostering a deeper comprehension of the relationship between a circle's radius and its circumference. |
Area and Circumference |
|
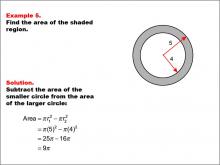
Math Example--Area and Perimeter--Circular Area and Circumference: Example 5 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 5TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units. The task is to calculate the area of the shaded region between these circles. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * (4)2 = 25π - 16π = 9π. Concentric circles and shaded regions introduce students to more complex geometric concepts. This example builds upon basic circular area calculations, encouraging students to think about the relationships between different circles and how to find areas of composite shapes. |
Area and Circumference |
|
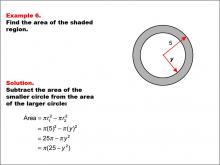
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 6TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2). |
Area and Circumference |
|
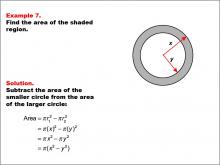
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 7TopicGeometry DescriptionThis example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2). |
Area and Circumference |
|
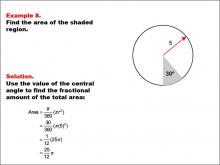
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 8TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12. |
Area and Circumference |

|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 9TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6. |
Area and Circumference |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 1 | Math Example--Area and Perimeter--Quadrilaterals: Example 1TopicGeometry DescriptionThis example demonstrates how to calculate the area of a square. The square ABCD has sides measuring 3 units each. To find the area, we use the formula A = s², where s is the length of a side. In this case, A = 3² = 9 square units. Understanding area and perimeter of quadrilaterals is a fundamental concept in geometry. This collection of examples helps students grasp these concepts by providing visual representations and step-by-step calculations for various quadrilaterals. By exploring different shapes and sizes, students develop a deeper understanding of how dimensions relate to area and perimeter. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 10 | Math Example--Area and Perimeter--Quadrilaterals: Example 10TopicGeometry DescriptionThis example demonstrates the calculation of a rhombus's area using algebraic expressions. The rhombus has a base of x + 6 units and a height of x - 2 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 6)(x - 2) = x² + 4x - 12 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 11 | Math Example--Area and Perimeter--Quadrilaterals: Example 11TopicGeometry DescriptionThis example illustrates how to calculate the area of a kite using its diagonals. The kite has diagonals measuring 25 units and 19 units. To find the area of a kite, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = (25 × 19) ÷ 2 = 475 ÷ 2 = 237.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 12 | Math Example--Area and Perimeter--Quadrilaterals: Example 12TopicGeometry DescriptionThis example demonstrates the calculation of a kite's area using algebraic expressions for its diagonals. The kite has diagonals measuring x + 11 units and x - 5 units. To find the area, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = [(x + 11)(x - 5)] ÷ 2 = (x² + 6x - 55) ÷ 2 = ½x² + 3x - 27.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 13 | Math Example--Area and Perimeter--Quadrilaterals: Example 13TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a square. The square ABCD has sides measuring 6 units each. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 6 = 24 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 14 | Math Example--Area and Perimeter--Quadrilaterals: Example 14TopicGeometry DescriptionThis example illustrates the calculation of a square's perimeter using an algebraic expression. The square ABCD has sides measuring x + 15 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 15) = 4x + 60 units. Incorporating algebra into geometry problems helps students connect different mathematical concepts and develop more advanced problem-solving skills. This collection of examples bridges the gap between basic geometry and algebraic thinking, preparing students for more complex mathematical challenges they will encounter in higher-level courses. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 15 | Math Example--Area and Perimeter--Quadrilaterals: Example 15TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rectangle. The rectangle ABCD has a length of 18 units and a width of 12 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2(18 + 12) = 2(30) = 60 units. |
Area and Perimeter of Quadrilaterals |