
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 4: Tables, Equations, and Graphs of Functions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
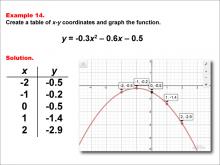
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 14 | Quadratic Functions in Tabular and Graph Form: Example 14TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. This example shows the symmetry of the parabola and how the vertex acts as a turning point, which is critical for graph analysis and interpretation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
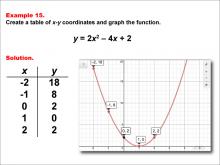
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 15 | Quadratic Functions in Tabular and Graph Form: Example 15TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The graph clearly shows the parabola's opening direction and the impact of the quadratic term, aiding in the comprehension of graph transformations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
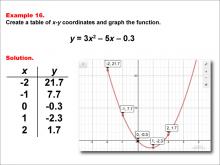
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 16 | Quadratic Functions in Tabular and Graph Form: Example 16TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The example demonstrates how the vertex form of the equation can be used to predict the graph's position and shape, enhancing understanding of vertex transformations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
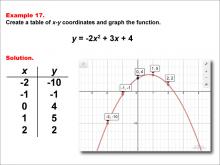
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 17 | Quadratic Functions in Tabular and Graph Form: Example 17TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The graphic representation is useful for identifying roots and how they correspond to the x-intercepts of the graph, which is fundamental for solving quadratic equations graphically. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
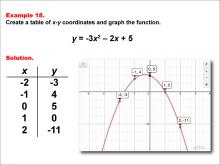
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 18 | Quadratic Functions in Tabular and Graph Form: Example 18TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The graphical representation is useful for determining the kind of discriminant and the number of roots, which is visually represented by the points where the graph intersects the x-axis. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
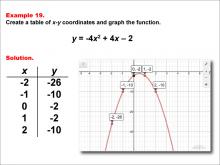
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 19 | Quadratic Functions in Tabular and Graph Form: Example 19TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. These representations are useful to show the axis of symmetry can be used to find the vertex and how this symmetry is reflected in the graph. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
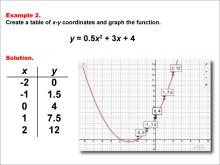
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 2 | Quadratic Functions in Tabular and Graph Form: Example 3TopicQuadratics DescriptionThis example demonstrates the concept of quadratic functions through a table of values and its graph. It emphasizes how the quadratic function translates into a parabolic graph, showcasing the vertex and symmetry. This visual representation aids in comprehending the impact of coefficients on the graph's curvature and direction. Mastery of this concept involves skills in graphing, interpreting quadratic equations, and identifying key features such as intercepts and vertex. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
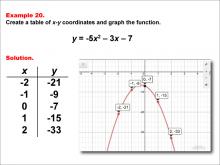
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 20 | Quadratic Functions in Tabular and Graph Form: Example 20TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. This example shows a downwardly opening parabola and you can see the relationship between the parameters of the function and how they are displayed graphically. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
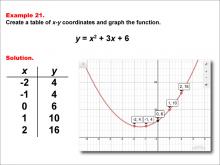
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 21 | Quadratic Functions in Tabular and Graph Form: Example 21TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The example shows an upwardly opening parabola. Make a note of the parameters of the function and how they are reflected in the table and graph. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
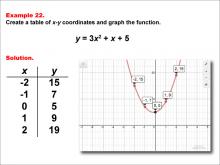
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 22 | Quadratic Functions in Tabular and Graph Form: Example 22TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The focus is on understanding how the graph's vertex and axis of symmetry relate to the equation, enhancing skills in graph interpretation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
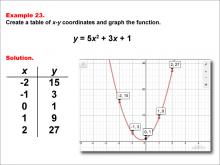
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 23 | Quadratic Functions in Tabular and Graph Form: Example 23TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. It demonstrates the role of the quadratic terms in determining the graph's curvature and the significance of intercepts in solving quadratic equations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
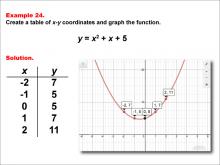
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 24 | Quadratic Functions in Tabular and Graph Form: Example 24TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The example shows an upwardly opening parabola and you can see the graph's symmetry and how it can be used to predict the function's behavior and solve equations graphically. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
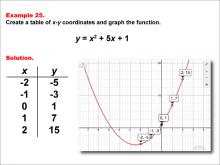
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 25 | Quadratic Functions in Tabular and Graph Form: Example 25TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. It highlights the alternative to the quadratic formula in finding roots and how these roots are represented graphically as x-intercepts. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
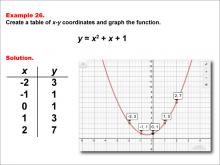
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 26 | Quadratic Functions in Tabular and Graph Form: Example 26TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The example shows a function with no roots, since the graph does not intersect the x-axis. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
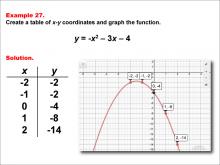
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 27 | Quadratic Functions in Tabular and Graph Form: Example 27TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The focus is on understanding how the graph's vertex and axis of symmetry relate to the equation, enhancing skills in graph interpretation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
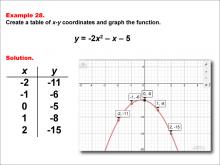
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 28 | Quadratic Functions in Tabular and Graph Form: Example 28TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. It demonstrates the role of the quadratic terms in determining the graph's curvature and the significance of intercepts in solving quadratic equations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
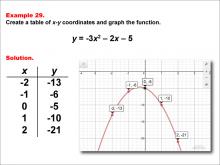
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 29 | Quadratic Functions in Tabular and Graph Form: Example 29TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. This example demonstrates the relationship between the quadratic equation and its graph, highlighting the vertex and axis of symmetry, which are key to understanding the function's behavior. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
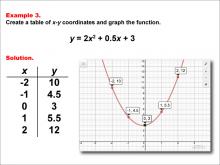
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 3 | Quadratic Functions in Tabular and Graph Form: Example 3TopicQuadratics DescriptionThis example illustrates a quadratic function through both a tabular data set and its corresponding graph. The table presents specific input-output pairs that, when plotted, form a parabolic curve on the graph. This visual representation highlights the quadratic function's key features, such as the vertex, axis of symmetry, and intercepts. The table allows for a clear understanding of how each value corresponds to a point on the graph, demonstrating the function's behavior over a range of inputs. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
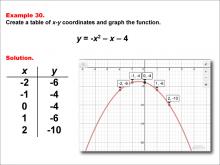
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 30 | Quadratic Functions in Tabular and Graph Form: Example 30TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The example illustrates how changes in coefficients affect the parabola's direction and width, providing insight into graph transformations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
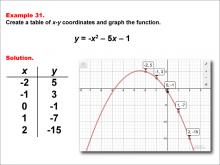
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 31 | Quadratic Functions in Tabular and Graph Form: Example 31TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. This example shows a downwardly opening parabola. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
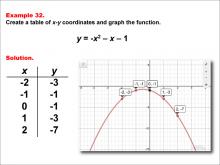
|
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 32 | Quadratic Functions in Tabular and Graph Form: Example 32TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The graph and table illustrate the importance of intercepts and how they relate to the roots of the quadratic equation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
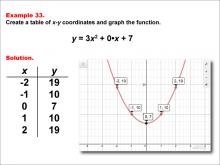
|
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 33 | Quadratic Functions in Tabular and Graph Form: Example 33TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. This example shows an upwardly opening parabola that doesn't intersect the x-axis. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
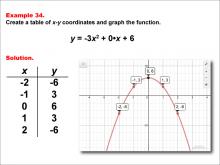
|
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 34 | Quadratic Functions in Tabular and Graph Form: Example 34TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. This example shows a downwardly opening parabola that intersects the x-axis at two points. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
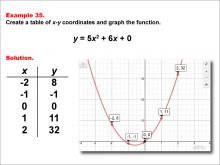
|
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 35 | Quadratic Functions in Tabular and Graph Form: Example 35TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The example shows an upwardly opening parabola that intersects the x-axis at two points. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
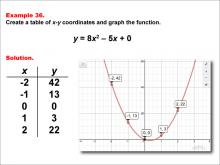
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 36 | Quadratic Functions in Tabular and Graph Form: Example 36TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. It demonstrates the role of the quadratic terms in determining the graph's curvature and the significance of intercepts in solving quadratic equations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
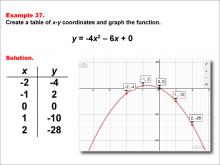
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 37 | Quadratic Functions in Tabular and Graph Form: Example 37TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. This example shows a downwardly opening parabola that has two roots, one of them shown in the table. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
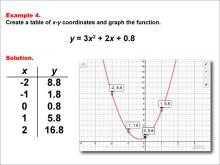
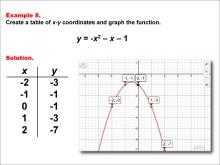
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 4 | Quadratic Functions in Tabular and Graph Form: Example 4TopicQuadratics |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
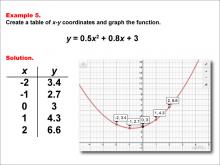
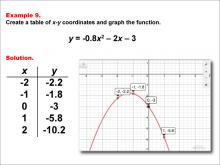
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 5 | Quadratic Functions in Tabular and Graph Form: Example 5TopicQuadratics DescriptionThis example provides a quadratic function displayed in both tabular and graphical forms. The table lists values that, when plotted, create a parabolic curve on the graph. This visual representation helps in identifying key features such as the vertex, axis of symmetry, and roots. By analyzing these features, students can understand the impact of different coefficients on the shape and position of the parabola. Skills involved include interpreting data from tables, graphing functions, and understanding the vertex and standard forms of quadratic equations. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 6 | Quadratic Functions in Tabular and Graph Form: Example 6TopicQuadratics DescriptionIn this example, a quadratic function is presented through both tabular and graphical forms. The accompanying image provides a visual interpretation of the function, emphasizing the relationship between the x-values and their corresponding y-values. This representation allows learners to recognize the nature of quadratic functions, particularly how changes to the function parameters affect the shape and position of the graph. The skills required include critical graph analysis, understanding symmetry in parabolas, and solving for x-intercepts. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 7 | Quadratic Functions in Tabular and Graph Form: Example 7TopicQuadratics DescriptionA detailed view of a quadratic function is depicted here, where the data table and graph work in conjunction to showcase the solution process for the function. Analyzing this illustration aids in comprehending how the quadratic function applies to specific scenarios and enhances one’s ability to derive equations from graphs. Such comparative analysis of multiple representations bolsters problem-solving skills and equips students with the tools to tackle different forms of quadratic equations. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 8 | Quadratic Functions in Tabular and Graph Form: Example 8TopicQuadratics DescriptionThis image presents a quadratic function in tabular and graphic format. The graph reflects the nature of parabolic functions, while the table reinforces the numerical data needed for graphing. By exploring both representations, students can appreciate the convergence of algebra and geometry, honing their capacity for critical thinking and analysis. Understanding the properties of the parabola is essential for mastery in quadratic equations by applying skills such as completing the square or using the quadratic formula. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
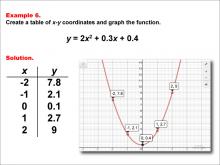
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 9 | Quadratic Functions in Tabular and Graph Form: Example 9TopicQuadratics DescriptionThis example consolidates the properties of quadratic functions by using a table to present values and a graph to illustrate their relationship. The significance of identifying intercepts, the vertex, and axis of symmetry becomes apparent when viewed together. Mastering these concepts through multiple formats allows for invaluable preparation for advanced algebraic topics, thereby enhancing overall mathematical comprehension and problem-solving abilities. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
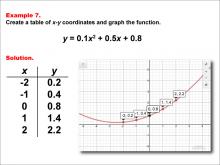
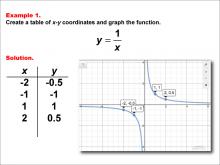
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 1 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 1TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / x. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph is a hyperbola with branches in the first and third quadrants, illustrating the characteristic shape of this basic rational function. |
Rational Functions and Equations |
|
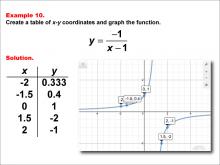
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 10 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 10TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = -1 / (x - 1). The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph includes labeled points at certain coordinates, illustrating how the negative sign in the numerator and the constant in the denominator affect the graph's shape and position. |
Rational Functions and Equations |
|
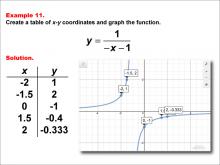
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 11 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 11TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x - 1). The image showcases both the table of x-y coordinates and the resulting graph. The graph is plotted with labeled points at given coordinates, illustrating how the negative sign and constant in the denominator affect the graph's shape and position. |
Rational Functions and Equations |
|
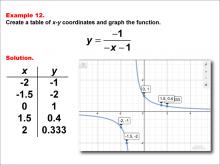
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 12 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 12TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x - 1). The image presents both the table of x-y coordinates and the resulting graph. The graph includes points labeled at specified coordinates, demonstrating how the negative signs in both the numerator and denominator, along with the constant, affect the graph's shape and position. |
Rational Functions and Equations |
|
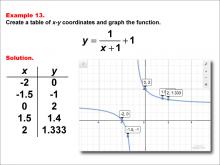
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 13 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 13TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (x + 1) + 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The table contains specific x-y coordinates: (-2, 0), (-1.5, -1), (0, 2), (1.5, 1.4), (2, 1.333), which are plotted on the graph. This example illustrates how adding a constant to a rational function affects its graph. |
Rational Functions and Equations |
|
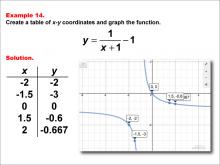
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 14 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 14TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (x + 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, -2), (-1.5, -3), (0, 0), (1.5, -0.6), (2, -0.667), which are plotted on the graph. This example illustrates how subtracting a constant from a rational function affects its graph. |
Rational Functions and Equations |
|
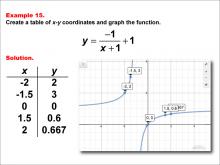
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 15 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 15TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (x + 1) + 1. The image presents both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, 2), (-1.5, 3), (0, 0), (1.5, 0.6), (2, 0.667), which are plotted on the graph. This example demonstrates how negating the numerator of a rational function and adding a constant affects its graph. |
Rational Functions and Equations |
|
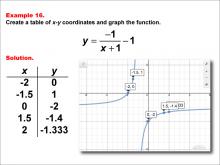
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 16 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 16TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = -1 / (x + 1) - 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The table contains specific x-y coordinates: (-2, 0), (-1.5, 1), (0, -2), (1.5, -1.4), (2, -1.333), which are plotted on the graph. This example illustrates how negating the numerator of a rational function and subtracting a constant affects its graph. |
Rational Functions and Equations |
|
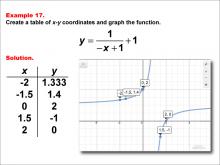
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 17 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 17TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x + 1) + 1. The image showcases both the table of x-y coordinates and the resulting graph. Points plotted include (-2, 1.333), (-1.5, 1.4), (0, 2), (1.5, -1), and (2, 0). The graph features a hyperbola with asymptotes, illustrating how negating the x-term in the denominator and adding a constant affects the graph's shape and position. |
Rational Functions and Equations |
|
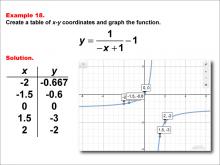
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 18 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 18TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x + 1) - 1. The image presents both the table of x-y coordinates and the resulting graph. Points plotted include (-2, -0.667), (-1.5, -0.6), (0, 0), (1.5, -3), and (2, -2). The graph shows a hyperbola with vertical and horizontal shifts, demonstrating how negating the x-term in the denominator and subtracting a constant affects the graph's shape and position. |
Rational Functions and Equations |
|
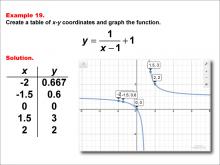
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 19 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 19TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (x - 1) + 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. Points include (-2, 0.667), (-1.5, 0.6), (0, 0), (1.5, 3), and (2, 2). The graph is a hyperbola with asymptotes at x = 1 and y = 1, illustrating how subtracting a constant in the denominator and adding a constant to the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
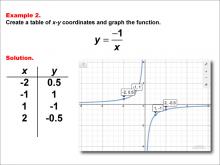
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 2 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 2TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / x. The image showcases both the table of x-y coordinates and the resulting graph. The graph is a hyperbola with branches in the second and fourth quadrants, illustrating how the negative sign affects the function's shape compared to the previous example. |
Rational Functions and Equations |
|
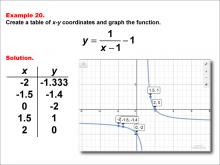
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 20 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 20TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (x - 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, -1.333), (-1.5, -1.4), (0, -2), (1.5, 1), and (2, 0). The graph is a hyperbola with shifted asymptotes at x = 1 and y = -1, illustrating how subtracting a constant in the denominator and from the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
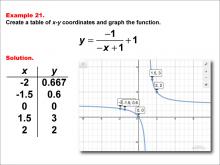
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 21 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 21TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = (-1) / (-x + 1) + 1. The image presents both the table of x-y coordinates and the resulting graph. It includes a table of x-y coordinates: (-2, 0.667), (-1.5, 0.6), (0, 0), (1.5, 3), and (2, 2). The graph is plotted on a grid, demonstrating how negating both the numerator and x-term in the denominator, while adding a constant to the entire fraction, affects the graph's shape and position. |
Rational Functions and Equations |
|
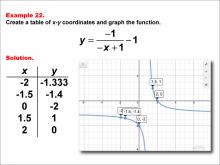
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 22 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 22TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = (-1) / (-x + 1) - 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. It includes a table of x-y coordinates: (-2, -1.333), (-1.5, -1.4), (0, -2), (1.5, 1), and (2, 0). The graph is plotted on a grid, illustrating how negating both the numerator and x-term in the denominator, while subtracting a constant from the entire fraction, affects the graph's shape and position. |
Rational Functions and Equations |
|
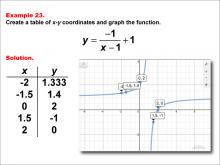
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 23 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 23TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = (-1) / (x - 1) + 1. The image shows both a table of x-y coordinates and the corresponding graph. The table includes points such as (-2, 1.333), (-1.5, 1.4), (0, 2), (1.5, -1), and (2, 0). The graph is plotted on a grid, illustrating how subtracting a constant in the denominator and adding a constant to the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
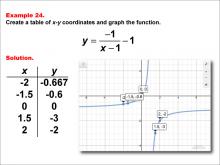
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 24 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 24TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = (-1) / (x - 1) - 1. The image shows both a table of x-y coordinates and the corresponding graph. The table includes points such as (-2, -0.667), (-1.5, -0.6), (0, 0), (1.5, -3), and (2, -2). The graph is plotted on a grid, illustrating how subtracting constants both in the denominator and from the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
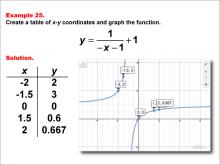
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 25 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 25TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x - 1) + 1. The image showcases both the table of x-y coordinates and the resulting graph. The graph shows points plotted at (-2, 2), (-1.5, 3), (0, 0), (1.5, 0.6), and (2, 0.667), illustrating how negating both terms inside the parentheses and adding a constant to the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |