
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 4: Tables, Equations, and Graphs of Functions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
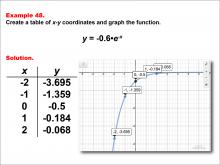
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 48 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 48TopicExponential Functions DescriptionThis example presents the exponential function y = -0.5 * e-x through a graph and table of x-y coordinates. The table provides points (-2, -3.695), (-1, -1.359), (0, -0.5), (1, -0.184), and (2, -0.068), which are plotted on the accompanying graph. Students are tasked with creating this table and graph to visualize the function's behavior. |
Graphs of Exponential and Logarithmic Functions |
|
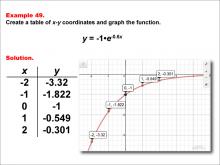
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 49 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 49TopicExponential Functions DescriptionThis example illustrates the exponential function y = -1 * e-0.6x through a graph and table of x-y coordinates. The table provides points (-2, -3.32), (-1, -1.822), (0, -1), (1, -0.549), and (2, -0.301), which are plotted on the accompanying graph. Students are challenged to create this table and graph to visualize the function's behavior. |
Graphs of Exponential and Logarithmic Functions |
|
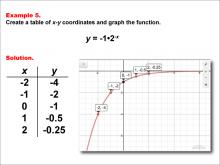
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 5 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 5TopicExponential Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the exponential function y = -1 * 2-x. The image presents both a table of values and a graph plotted on a coordinate plane, with points labeled for x values from -2 to 2. This representation helps students visualize the behavior of a decreasing exponential function with a negative coefficient. |
Graphs of Exponential and Logarithmic Functions |
|
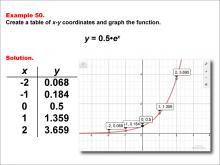
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 50 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 50TopicExponential Functions DescriptionThis example showcases the exponential function y = 0.5 * ex through a graph and table of x-y coordinates. The table provides points (-2, 0.068), (-1, 0.184), (0, 0.5), (1, 1.359), and (2, 3.695), which are plotted on the accompanying graph. Students are tasked with creating this table and graph to visualize the function's behavior. |
Graphs of Exponential and Logarithmic Functions |
|
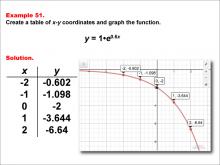
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 51 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 51TopicExponential Functions DescriptionThis example illustrates the exponential function y = e0.6x through a graph and table of x-y coordinates. The table provides points (-2, -0.602), (-1, -1.098), (0, -2), (1, -3.644), and (2, -6.64), which are plotted on the accompanying graph. Students are challenged to create this table and graph to visualize the function's behavior. |
Graphs of Exponential and Logarithmic Functions |
|
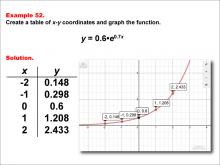
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 52 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 52TopicExponential Functions DescriptionThis example showcases the exponential function y = 0.6 * e0.7x through a graph and table of x-y coordinates. The table provides points (-2, 0.148), (-1, 0.298), (0, 0.6), (1, 1.208), and (2, 2.433), which are plotted on the accompanying graph. Students are tasked with creating this table and graph to visualize the function's behavior. |
Graphs of Exponential and Logarithmic Functions |
|
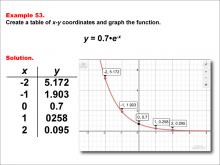
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 53 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 53TopicExponential Functions DescriptionThis example illustrates the exponential function y = 0.7 * e-x through a graph and table of x-y coordinates. The table provides points (-2, 5.172), (-1, 1.903), (0, 0.7), (1, 0.258), and (2, 0.095), which are plotted on the accompanying graph showing a decreasing curve. Students are challenged to create this table and graph to visualize the function's behavior. |
Graphs of Exponential and Logarithmic Functions |
|
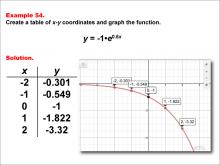
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 54 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 54TopicExponential Functions DescriptionThis example presents the exponential function y = -1 * e0.6x through a graph and table of x-y coordinates. The table provides points (-2, -0.301), (-1, -0.549), (0, -1), (1, -1.822), and (2, -3.32), which are plotted on the accompanying graph showing a decreasing curve. Students are tasked with creating this table and graph to visualize the function's behavior. |
Graphs of Exponential and Logarithmic Functions |
|
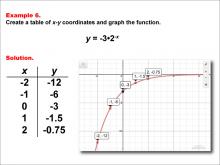
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 6 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 6TopicExponential Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the exponential function y = -3 * 2-x. The image provides both a table of values and a graph plotted on a coordinate plane, with points labeled for x values ranging from -2 to 2. This representation helps students visualize the behavior of a decreasing exponential function with a negative coefficient and a larger magnitude. |
Graphs of Exponential and Logarithmic Functions |
|
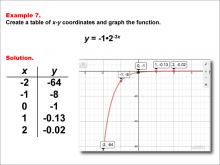
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 7 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 7TopicExponential Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the exponential function y = -1 * 2-3x. The image presents both a table of values and a graph plotted on a coordinate plane, with points labeled for x values from -2 to 2. This representation helps students visualize the behavior of a decreasing exponential function with a negative coefficient and a factor in the exponent. |
Graphs of Exponential and Logarithmic Functions |
|
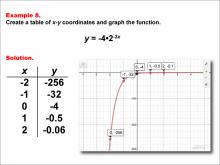
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 8 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 8TopicExponential Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the exponential function y = -4 * 2-3x. The image provides both a table of values and a graph plotted on a coordinate plane, with points labeled for x values ranging from -2 to 2. This representation helps students visualize the behavior of a decreasing exponential function with a negative coefficient, a larger magnitude, and a factor in the exponent. |
Graphs of Exponential and Logarithmic Functions |
|
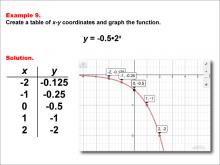
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 9 | Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 9TopicExponential Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the exponential function y = -0.5 * 2x. The image presents both a table of values and a graph, displaying the function's behavior. The table lists x-y coordinates for x values from -2 to 2, with corresponding y values calculated using the given function. This representation helps students visualize an exponential function with a negative fractional coefficient. |
Graphs of Exponential and Logarithmic Functions |
|
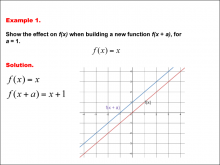
Math Example--Function Concepts--Building Functions: Example 1 | Math Example--Function Concepts--Building Functions: Example 1TopicArithmetic DescriptionAnalyze the effect of building a new function f(x + a) from f(x) = x, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x shifts horizontally by adding a to the input. substituting a = 1, the new function becomes f(x + a) = x + 1. the graph shifts one unit up. |
Relations and Functions |
|
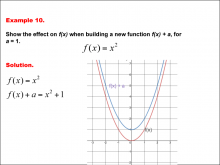
Math Example--Function Concepts--Building Functions: Example 10 | Math Example--Function Concepts--Building Functions: Example 10TopicArithmetic DescriptionAnalyze the effect of building a new function f(x) + a from f(x) = x2, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x2 shifts vertically by adding a to the output. substituting a = 1, the new function becomes f(x) + a = x2 + 1. the graph shifts one unit upward. |
Relations and Functions |
|
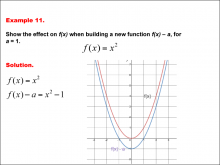
Math Example--Function Concepts--Building Functions: Example 11 | Math Example--Function Concepts--Building Functions: Example 11TopicArithmetic DescriptionThe problem involves analyzing the effect on the function f(x) = x2 when a constant a is subtracted. The specific scenario is for a = 1. The goal is to determine how the graph of f(x) is transformed. This example shows the effect on the function when subtracting a constant a from f(x) shifts the graph of f(x) downward by a units. for a = 1, the function becomes f(x) - a = x2 - 1. this results in a vertical shift down, as shown by the new graph in blue compared to the original in red. |
Relations and Functions |
|
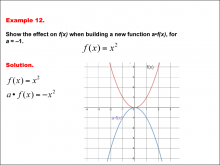
Math Example--Function Concepts--Building Functions: Example 12 | Math Example--Function Concepts--Building Functions: Example 12TopicArithmetic DescriptionThe problem examines the effect on the function f(x) = x2 when it is scaled by a constant a. The specific case here is a = -1. The goal is to describe the transformation caused by the scaling. This example shows the effect on the function when multiplying f(x) by a constant a reflects the graph across the x-axis if a < 0. for a = -1, the function becomes a * f(x) = -x2. this results in a reflection of the original graph (in red) to the inverted graph (in blue). |
Relations and Functions |
|
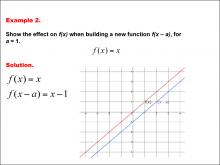
Math Example--Function Concepts--Building Functions: Example 2 | Math Example--Function Concepts--Building Functions: Example 2TopicArithmetic DescriptionAnalyze the effect of building a new function f(x - a) from f(x) = x, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x shifts horizontally by subtracting a from the input. substituting a = 1, the new function becomes f(x - a) = x - 1. the graph shifts one unit down. |
Relations and Functions |
|
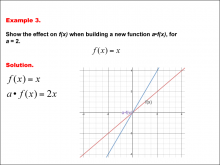
Math Example--Function Concepts--Building Functions: Example 3 | Math Example--Function Concepts--Building Functions: Example 3TopicArithmetic DescriptionAnalyze the effect of building a new function a * f(x) from f(x) = x, where a = 2. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x scales vertically by multiplying the output by a. substituting a = 2, the new function becomes a * f(x) = 2x. the graph is stretched vertically. |
Relations and Functions |
|
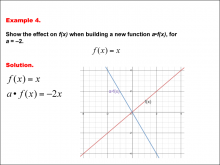
Math Example--Function Concepts--Building Functions: Example 4 | Math Example--Function Concepts--Building Functions: Example 4TopicArithmetic DescriptionAnalyze the effect of building a new function a * f(x) from f(x) = x, where a = -2. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x scales vertically and reflects across the x-axis due to the negative value of a. substituting a = -2, the new function becomes a * f(x) = -2x. the graph is reflected and stretched vertically. |
Relations and Functions |
|
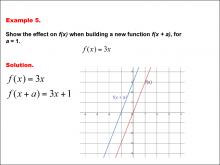
Math Example--Function Concepts--Building Functions: Example 5 | Math Example--Function Concepts--Building Functions: Example 5TopicArithmetic DescriptionAnalyze the effect of building a new function f(x + a) from f(x) = 3x, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = 3x shifts horizontally by adding a to the input. substituting a = 1, the new function becomes f(x + a) = 3x + 1. the graph shifts one unit up. |
Relations and Functions |
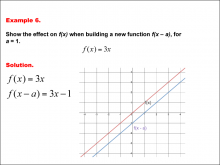
|
Math Example--Function Concepts--Building Functions: Example 6 | Math Example--Function Concepts--Building Functions: Example 6TopicArithmetic DescriptionAnalyze the effect of building a new function f(x - a) from f(x) = 3x, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = 3x shifts horizontally by subtracting a from the input. substituting a = 1, the new function becomes f(x - a) = 3x - 1. the graph shifts one unit down. |
Relations and Functions |
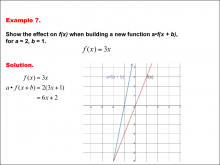
|
Math Example--Function Concepts--Building Functions: Example 7 | Math Example--Function Concepts--Building Functions: Example 7TopicArithmetic DescriptionAnalyze the effect of building a new function a * f(x + b) from f(x) = 3x, where a = 2 and b = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = 3x first shifts horizontally by adding b to the input, and then scales vertically by a. substituting a = 2 and b = 1, the new function becomes a * f(x + b) = 6x + 2. the graph is shifted and stretched vertically. |
Relations and Functions |
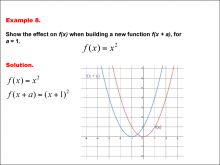
|
Math Example--Function Concepts--Building Functions: Example 8 | Math Example--Function Concepts--Building Functions: Example 8TopicArithmetic DescriptionAnalyze the effect of building a new function f(x + a) from f(x) = x2, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x2 shifts horizontally by adding a to the input. substituting a = 1, the new function becomes f(x + a) = (x + 1)2. the graph shifts one unit to the left. |
Relations and Functions |
|
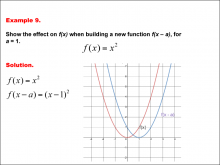
Math Example--Function Concepts--Building Functions: Example 9 | Math Example--Function Concepts--Building Functions: Example 9TopicArithmetic DescriptionAnalyze the effect of building a new function f(x - a) from f(x) = x2, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x2 shifts horizontally by subtracting a from the input. substituting a = 1, the new function becomes f(x - a) = (x - 1)2. the graph shifts one unit to the right. |
Relations and Functions |
|
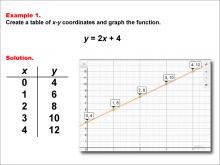
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 1 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 1TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 2x + 4. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 4), (1, 6), (2, 8), (3, 10), and (4, 12), illustrating how the y-value increases by 2 for each unit increase in x. |
Graphs of Linear Functions |
|
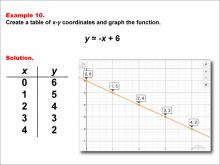
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 10 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 10TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -x + 6. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 6), (1, 5), (2, 4), (3, 3), and (4, 2), illustrating how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
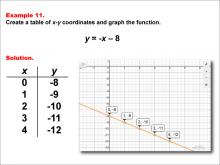
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 11 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 11TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = -x - 8. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -8), (1, -9), (2, -10), (3, -11), and (4, -12), showing how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
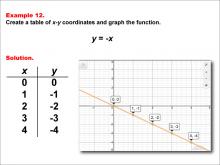
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 12 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 12TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = -x. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -1), (2, -2), (3, -3), and (4, -4), illustrating how the y-value decreases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
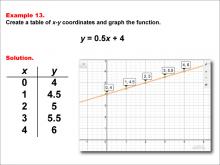
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 13 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 13TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0.5x + 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 4), (1, 4.5), (2, 5), (3, 5.5), and (4, 6), showing how the y-value increases by 0.5 for each unit increase in x. |
Graphs of Linear Functions |
|
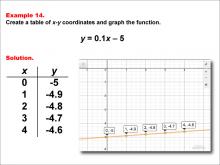
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 14 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 14TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 0.1x - 5. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, -5), (1, -4.9), (2, -4.8), (3, -4.7), and (4, -4.6), illustrating how the y-value increases by 0.1 for each unit increase in x. |
Graphs of Linear Functions |

|
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 15 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 15TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0.2x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 0.2), (2, 0.4), (3, 0.6), and (4, 0.8), showing how the y-value increases by 0.2 for each unit increase in x. |
Graphs of Linear Functions |
|
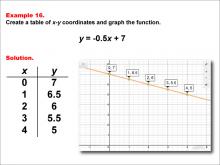
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 16 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 16TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -0.5x + 7. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 7), (1, 6.5), (2, 6), (3, 5.5), and (4, 5), illustrating how the y-value decreases by 0.5 for each unit increase in x. |
Graphs of Linear Functions |
|
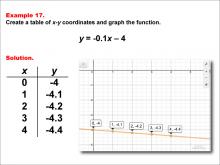
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 17 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 17TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = -0.1x - 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -4), (1, -4.1), (2, -4.2), (3, -4.3), and (4, -4.4), showing how the y-value decreases by 0.1 for each unit increase in x. |
Graphs of Linear Functions |
|
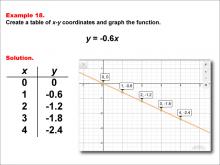
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 18 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 18TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -0.6x. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -0.6), (2, -1.2), (3, -1.8), and (4, -2.4), illustrating how the y-value decreases by 0.6 for each unit increase in x. |
Graphs of Linear Functions |
|
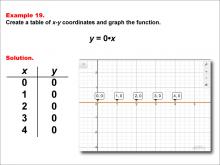
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 19 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 19TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 0), (2, 0), (3, 0), and (4, 0), showing how the y-value remains constant at 0 for all values of x. |
Graphs of Linear Functions |
|
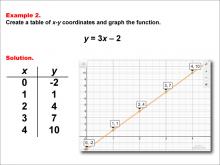
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 2 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 2TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 3x - 2. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, -2), (1, 1), (2, 4), (3, 7), and (4, 10), showing how the y-value increases by 3 for each unit increase in x. |
Graphs of Linear Functions |
|
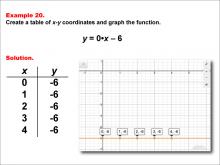
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 20 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 20TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = 0x - 6. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, -6), (1, -6), (2, -6), (3, -6), and (4, -6), illustrating how the y-value remains constant at -6 for all values of x. |
Graphs of Linear Functions |
|
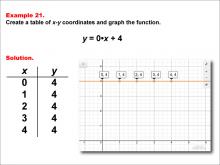
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 21 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 21TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = 0 * x + 4. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 4), (1, 4), (2, 4), (3, 4), and (4, 4), showing how the y-value remains constant at 4 for all values of x. |
Graphs of Linear Functions |
|
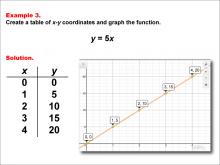
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 3 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 3TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = 5x. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, 5), (2, 10), (3, 15), and (4, 20), illustrating how the y-value increases by 5 for each unit increase in x. |
Graphs of Linear Functions |
|
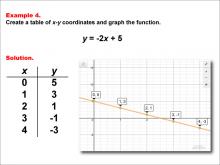
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 4 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 4TopicLinear Functions DescriptionThis example showcases the process of creating a table of x-y coordinates and graphing the linear function y = -2x + 5. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 5), (1, 3), (2, 1), (3, -1), and (4, -3), demonstrating how the y-value decreases by 2 for each unit increase in x. |
Graphs of Linear Functions |
|
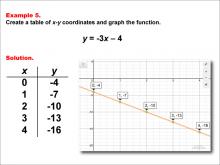
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 5 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 5TopicLinear Functions DescriptionThis example illustrates the creation of a table of x-y coordinates and the graphing of the linear function y = -3x - 4. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, -4), (1, -7), (2, -10), (3, -13), and (4, -16), showing how the y-value decreases by 3 for each unit increase in x. |
Graphs of Linear Functions |
|
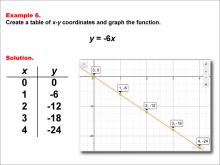
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 6 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 6TopicLinear Functions DescriptionThis example demonstrates how to create a table of x-y coordinates and graph the linear function y = -6x. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -6), (2, -12), (3, -18), and (4, -24), illustrating how the y-value decreases by 6 for each unit increase in x. |
Graphs of Linear Functions |
|
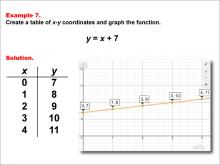
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 7 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 7TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = x + 7. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 7), (1, 8), (2, 9), (3, 10), and (4, 11), showing how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
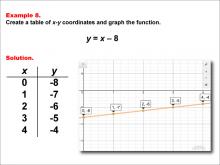
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 8 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 8TopicLinear Functions DescriptionThis example demonstrates the creation of a table of x-y coordinates and the graphing of the linear function y = x - 8. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, -8), (1, -7), (2, -6), (3, -5), and (4, -4), illustrating how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
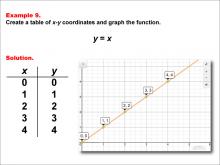
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 9 | Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 9TopicLinear Functions DescriptionThis example illustrates the process of creating a table of x-y coordinates and graphing the linear function y = x. The image presents both a graph and a table for this function. The table includes coordinate pairs (0, 0), (1, 1), (2, 2), (3, 3), and (4, 4), showing how the y-value increases by 1 for each unit increase in x. |
Graphs of Linear Functions |
|
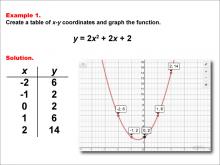
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 1 | Quadratic Functions in Tabular and Graph Form: Example 2TopicQuadratics DescriptionThis example illustrates the relationship between quadratic functions and their graphical representations. The image shows a table of values and the corresponding graph of a quadratic function, highlighting how changes in the equation affect the graph's shape and position. Understanding this relationship is crucial for interpreting and predicting the behavior of quadratic functions. Skills involved include plotting points, recognizing parabolic shapes, and analyzing vertex and axis of symmetry. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
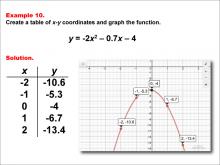
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 10 | Quadratic Functions in Tabular and Graph Form: Example 10TopicQuadratics |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
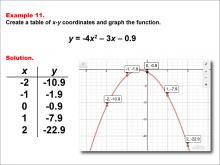
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 11 | Quadratic Functions in Tabular and Graph Form: Example 11TopicQuadratics |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
|
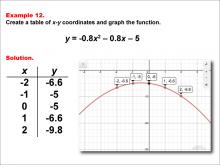
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 12 | Quadratic Functions in Tabular and Graph Form: Example 12TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. This example highlights the relationship between the equation and its graph, showing the parabolic curve and how it opens downward. Key features such as the vertex and intercepts are easily identifiable, which are crucial for understanding the function's behavior. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |
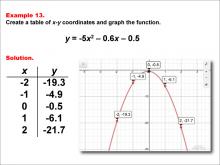
|
Math Example--Quadratics--Quadratic Functions in Tabular and Graph Form: Example 13 | Quadratic Functions in Tabular and Graph Form: Example 13TopicQuadratics DescriptionIn this example, a quadratic function is shown in tabular and graphic format. Analyzing these different representations of a function is important and provides relevant information about the quadratic function. The example illustrates how the coefficients in the quadratic equation affect the graph's shape and direction, allowing for a deeper understanding of the function's properties. |
Graphs of Quadratic Functions and Quadratic Equations and Functions |