
Illustrative Math Alignment: Grade 8 Unit 8
Pythagorean Theorem and Irrational Numbers
Lesson 7: A Proof of the Pythagorean Theorem
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
Math Examples Collection: Right Triangles | OverviewThe Media4Math collection on Right Triangles offers a comprehensive set of examples designed to enhance students' understanding of this fundamental geometric concept. These examples cover a wide range of skills, including applying the Pythagorean theorem, using trigonometric ratios, and solving real-world problems involving right triangles. |
Right Triangles |
|
Math Definitions Collection: Geometry Theorems and Postulates |
OverviewThis collection aggregates all the definition image cards around the topic of Theorems and Postulates terms and vocabulary. There are a total of 18 terms. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation.
|
Definition of a Triangle, Definition of an Angle, Right Triangles and Definition of a Line |

|
Math in the News Collection: Applications of Exponential Functions |
OverviewThis is a collection of Math in the News stories that focus on the topic of Exponential Functions.
|
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions, Data Analysis and Sequences |

|
Math in the News Collection: Business Math |
OverviewThis is a collection of issues of Math in the News that deal with business applications.
|
Applications of Exponential and Logarithmic Functions, Data Analysis and Volume |

|
Definition--Geometry Basics--Distance Formula | Distance FormulaTopicGeometry Basics DefinitionThe distance formula is used to determine the distance between two points in a coordinate plane. DescriptionThe distance formula is derived from the Pythagorean Theorem and is given by |
The Distance Formula |

|
Definition--Theorems and Postulates--Converse of the Pythagorean Theorem | Definition--Theorems and Postulates--Converse of the Pythagorean Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Right Triangles |

|
Definition--Theorems and Postulates--HL Theorem | Definition--Theorems and Postulates--HL Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Right Triangles |
|
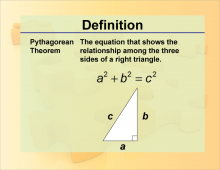
Definition--Theorems and Postulates--Pythagorean Theorem | Definition--Theorems and Postulates--Pythagorean Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Right Triangles |

|
INSTRUCTIONAL RESOURCE: Math Examples 46 | INSTRUCTIONAL RESOURCE: Math Examples--Right Triangles
This set of tutorials provides 26 examples of how to find the length of a side of a triangle using given angle or side measurements. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Right Triangles |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Constructing an Isosceles Triangle | In this Slide Show, we show how to construct an isosceles triangle. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Definition of a Triangle and Geometric Constructions with Triangles |

|
INSTRUCTIONAL RESOURCE: TI-Nspire App Activity: Constructing an Isosceles Triangle | In this Slide Show, learn how to use the TI-Nspire App to construct an isosceles triangle. Note: The download is a PPT file. |
Definition of a Triangle and Geometric Constructions with Triangles |

|
Interactive Crossword Puzzle--Quadrilaterals | Interactive Crossword Puzzle--Quadrilaterals
This interactive crossword puzzle tests knowledge of key terms on the topic of quadrilaterals. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Quadrilateral |

|
Interactive Crossword Puzzle--Triangles | Interactive Crossword Puzzle--Triangles
This interactive crossword puzzle tests knowledge of key terms on the topic of triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |
|
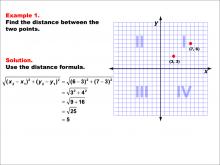
Math Example--Coordinate Geometry--Distance Formula: Example 1 | Math Example--Coordinate Geometry--Distance Formula: Example 1TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (3, 3) and (7, 6) are plotted on a graph, and the distance between them is calculated using the formula: √((6 - 3)2 + (7 - 3)2) = 5. |
The Distance Formula |
|
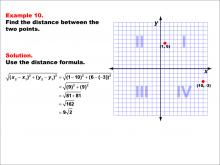
Math Example--Coordinate Geometry--Distance Formula: Example 10 | Math Example--Coordinate Geometry--Distance Formula: Example 10TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (1, 6) and (10, -3) are plotted on a graph, and the distance between them is determined using the formula: √((1 - 10)2 + (6 - (-3))2) = √(9^2 + 9^2) = √162 = 9√2. |
The Distance Formula |
|
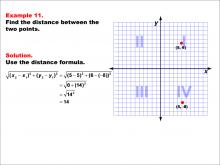
Math Example--Coordinate Geometry--Distance Formula: Example 11 | Math Example--Coordinate Geometry--Distance Formula: Example 11TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the vertical distance between two points on a coordinate plane. The points (5, 6) and (5, -8) are plotted on a graph, and the distance between them is calculated using the formula: √((5 - 5)2 + (6 - (-8))2) = √(0 + (14)2) = 14. |
The Distance Formula |
|
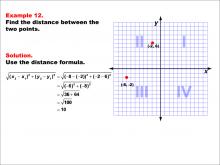
Math Example--Coordinate Geometry--Distance Formula: Example 12 | Math Example--Coordinate Geometry--Distance Formula: Example 12TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-8, -2) and (-2, 6) are plotted on a graph, and the distance between them is determined using the formula: √((-8 - (-2))2 + (-2 - 6)2) = √((-6)2 + (-8)2) = 10. |
The Distance Formula |
|
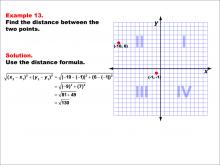
Math Example--Coordinate Geometry--Distance Formula: Example 13 | Math Example--Coordinate Geometry--Distance Formula: Example 13TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-10, 6) and (-1, -1) are plotted on a graph, and the distance between them is calculated using the formula: √((-10 - (-1))2 + (6 - (-1))2) = √((-9)2 + 72) = √130. |
The Distance Formula |
|
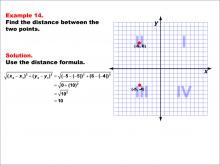
Math Example--Coordinate Geometry--Distance Formula: Example 14 | Math Example--Coordinate Geometry--Distance Formula: Example 14TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the vertical distance between two points on a coordinate plane. The points (-5, 6) and (-5, -4) are plotted on a graph, and the distance between them is determined using the formula: √((-5 - (-5))2 + (6 - (-4))2) = √(0 + 102) = 10. |
The Distance Formula |
|
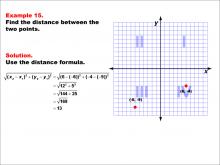
Math Example--Coordinate Geometry--Distance Formula: Example 15 | Math Example--Coordinate Geometry--Distance Formula: Example 15TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-6, -9) and (6, -4) are plotted on a graph, and the distance between them is calculated using the formula: √((6 - (-6))2 + (-4 - (-9))2) = √(122 + 52) = 13. |
The Distance Formula |
|
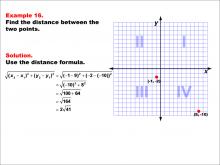
Math Example--Coordinate Geometry--Distance Formula: Example 16 | Math Example--Coordinate Geometry--Distance Formula: Example 16TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-1, -2) and (9, -10) are plotted on a graph, and the distance between them is determined using the formula: √((-1 - 9)2 + (-2 - (-10))2) = √((-10)2 + 82) = 2√41. |
The Distance Formula |
|
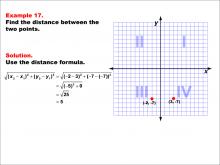
Math Example--Coordinate Geometry--Distance Formula: Example 17 | Math Example--Coordinate Geometry--Distance Formula: Example 17TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the horizontal distance between two points on a coordinate plane. The points (-2, -7) and (3, -7) are plotted on a graph, and the distance between them is calculated using the formula: √((-2 - 3)2 + (-7 + 7)2) = √((-5)2 + 0) = 5. |
The Distance Formula |
|
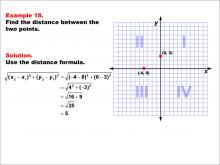
Math Example--Coordinate Geometry--Distance Formula: Example 18 | Math Example--Coordinate Geometry--Distance Formula: Example 18TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-4, 0) and (0, 3) are plotted on a graph, and the distance between them is determined using the formula: √((4 - 0)2 + (0 - 3)2) = √(16 + 9) = 5. |
The Distance Formula |
|
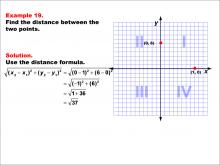
Math Example--Coordinate Geometry--Distance Formula: Example 19 | Math Example--Coordinate Geometry--Distance Formula: Example 19TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (0, 6) and (1, 0) are plotted on a graph, and the distance between them is calculated using the formula: √((0 - 1)2 + (6 - 0)2) = √(1 + 36) = √37. |
The Distance Formula |
|
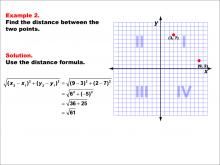
Math Example--Coordinate Geometry--Distance Formula: Example 2 | Math Example--Coordinate Geometry--Distance Formula: Example 2TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (3, 7) and (9, 2) are plotted on a graph, and the distance between them is determined using the formula: √((9 - 3)2 + (2 - 7)2) = √(61). |
The Distance Formula |
|
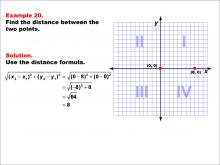
Math Example--Coordinate Geometry--Distance Formula: Example 20 | Math Example--Coordinate Geometry--Distance Formula: Example 20TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the horizontal distance between two points on a coordinate plane. The points (0, 0) and (8, 0) are plotted on a graph, and the distance between them is determined using the formula: √((0 - 8)2 + (0 - 0)2) = √64 = 8. |
The Distance Formula |
|
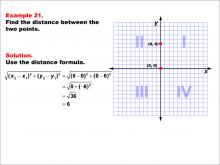
Math Example--Coordinate Geometry--Distance Formula: Example 21 | Math Example--Coordinate Geometry--Distance Formula: Example 21TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the vertical distance between two points on a coordinate plane. The points (0, 0) and (0, 6) are plotted on a graph, and the distance between them is calculated using the formula: √((0 - 0)2 + (0 - 6)2) = √(0 + (-6)2) = 6. |
The Distance Formula |
|
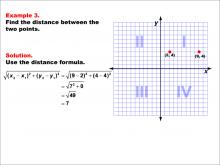
Math Example--Coordinate Geometry--Distance Formula: Example 3 | Math Example--Coordinate Geometry--Distance Formula: Example 3TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (2, 4) and (9, 4) are plotted on a graph, and the distance between them is calculated using the formula: √((9 - 2)2 + (4 - 4)2) = 7. |
The Distance Formula |
|
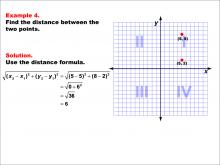
Math Example--Coordinate Geometry--Distance Formula: Example 4 | Math Example--Coordinate Geometry--Distance Formula: Example 4TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the vertical distance between two points on a coordinate plane. The points (5, 8) and (5, 2) are plotted on a graph, and the distance between them is determined using the formula: √((5 - 5)2 + (8 - 2)2) = 6. |
The Distance Formula |
|
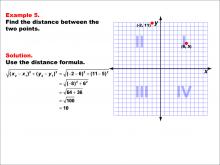
Math Example--Coordinate Geometry--Distance Formula: Example 5 | Math Example--Coordinate Geometry--Distance Formula: Example 5TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-2, 11) and (6, 5) are plotted on a graph, and the distance between them is calculated using the formula: √((-2 - 6)2 + (11 - 5)2) = 10. |
The Distance Formula |
|
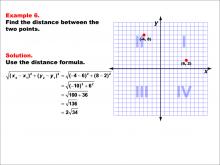
Math Example--Coordinate Geometry--Distance Formula: Example 6 | Math Example--Coordinate Geometry--Distance Formula: Example 6TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-4, 8) and (6, 2) are plotted on a graph, and the distance between them is determined using the formula: √((-4 - 6)2 + (8 - 2)2) = 2 √(34). |
The Distance Formula |
|
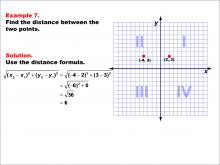
Math Example--Coordinate Geometry--Distance Formula: Example 7 | Math Example--Coordinate Geometry--Distance Formula: Example 7TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-4, 3) and (2, 3) are plotted on a graph, and the distance between them is calculated using the formula: √((-4 - 2)2 + (3 - 3)2) = 6. |
The Distance Formula |
|
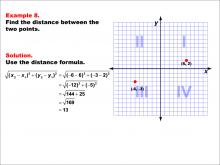
Math Example--Coordinate Geometry--Distance Formula: Example 8 | Math Example--Coordinate Geometry--Distance Formula: Example 8TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-6, -3) and (6, 2) are plotted on a graph, and the distance between them is determined using the formula: √((-6 - 6)2 + (-3 - 2)2) = 13. |
The Distance Formula |
|
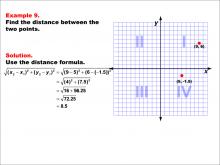
Math Example--Coordinate Geometry--Distance Formula: Example 9 | Math Example--Coordinate Geometry--Distance Formula: Example 9TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (9, 6) and (5, -1.5) are plotted on a graph, and the distance between them is calculated using the formula: √((9 - 5)2 + (6 - (-1.5))2) = √(4^2 + 7.5^2) = √72.25 = 8.5. |
The Distance Formula |
|
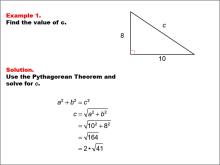
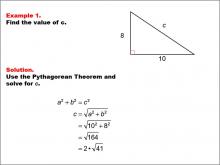
Math Example--Right Triangles-- Example 1 | Math Example--Right Triangles-- Example 1TopicRight Triangles DescriptionThis example presents a right triangle with sides of length 8 and 10, and an unknown hypotenuse labeled c. The task is to find the value of c using the Pythagorean Theorem. By applying the formula a2 + b2 = c2, we can calculate that c = √(102 + 82) = √(164) = 2 * √(41). |
Right Triangles |
|
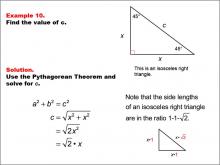
Math Example--Right Triangles-- Example 10 | Math Example--Right Triangles-- Example 10TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 11 | Math Example--Right Triangles-- Example 11TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 12 | Math Example--Right Triangles-- Example 12TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 13 | Math Example--Right Triangles-- Example 13TopicRight Triangles |
Right Triangles |
|
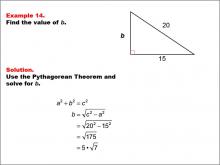
Math Example--Right Triangles-- Example 14 | Math Example--Right Triangles-- Example 14TopicRight Triangles |
Right Triangles |
|
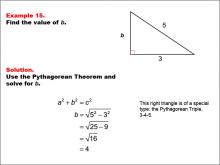
Math Example--Right Triangles-- Example 15 | Math Example--Right Triangles-- Example 15TopicRight Triangles |
Right Triangles |
|
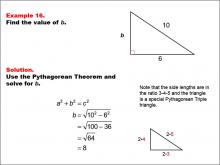
Math Example--Right Triangles-- Example 16 | Math Example--Right Triangles-- Example 16TopicRight Triangles |
Right Triangles |
|
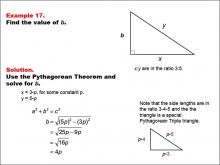
Math Example--Right Triangles-- Example 17 | Math Example--Right Triangles-- Example 17TopicRight Triangles |
Right Triangles |
|
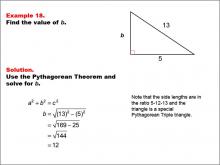
Math Example--Right Triangles-- Example 18 | Math Example--Right Triangles-- Example 18TopicRight Triangles |
Right Triangles |
|
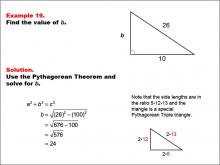
Math Example--Right Triangles-- Example 19 | Math Example--Right Triangles-- Example 19TopicRight Triangles |
Right Triangles |
|
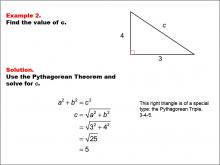
Math Example--Right Triangles-- Example 2 | Math Example--Right Triangles-- Example 2TopicRight Triangles DescriptionIn this example, we have a right triangle with sides of length 3 and 4, and an unknown hypotenuse labeled c. The goal is to determine the value of c using the Pythagorean Theorem. By applying the formula a2 + b2 = c2, we can calculate that c = √(32 + 42) = √(25) = 5. This example builds upon the previous one, reinforcing the application of the Pythagorean Theorem in right triangles. It demonstrates how the theorem can be used with different side lengths, helping students understand its versatility in solving various right triangle problems. |
Right Triangles |
|
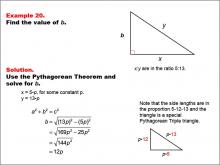
Math Example--Right Triangles-- Example 20 | Math Example--Right Triangles-- Example 20TopicRight Triangles |
Right Triangles |
|
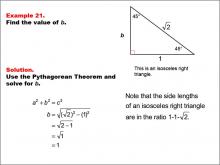
Math Example--Right Triangles-- Example 21 | Math Example--Right Triangles-- Example 21TopicRight Triangles |
Right Triangles |
|
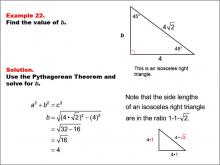
Math Example--Right Triangles-- Example 22 | Math Example--Right Triangles-- Example 22TopicRight Triangles |
Right Triangles |
|
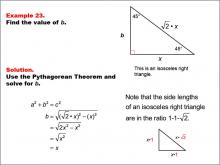
Math Example--Right Triangles-- Example 23 | Math Example--Right Triangles-- Example 23TopicRight Triangles |
Right Triangles |