
Illustrative Math Alignment: Grade 8 Unit 8
Pythagorean Theorem and Irrational Numbers
Lesson 9: The Converse
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
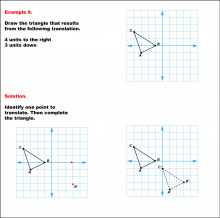
Math Example--Geometric Transformation--Translating Triangles--Example 9 | Math Example--Geometric Transformation--Translating Triangles--Example 9TopicTransformations DescriptionA triangle is translated 4 units to the right and 3 units down. The image shows both the original and the new triangle positions. Example 9: "Draw the triangle that results from the following translation: 4 units to the right, 3 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
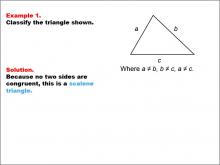
Math Example--Polygons--Triangle Classification: Example 1 | Math Example--Polygons--Triangle Classification: Example 1TopicTriangles DescriptionThis image shows a triangle with side lengths labeled as a, b, and c, where all sides are unequal. Based on the length of each side, the triangle is classified as scalene, as no two sides are congruent. Triangles are categorized based on side length (scalene, isosceles, equilateral) or angle measures (acute, obtuse, right). In this example, the scalene classification is determined by identifying that each side is a different length. The examples in this collection illustrate various classification rules based on both side and angle properties. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 10 | Math Example--Polygons--Triangle Classification: Example 10TopicTriangles DescriptionThis example presents a triangle with side lengths of 10, 10, and 8. Since two sides are congruent, the triangle is classified as isosceles. Triangle classification can be determined by side lengths or angle measures. Isosceles triangles have two equal sides or angles. Reviewing different examples assists students in identifying these types based on side or angle properties. Seeing multiple worked-out examples reinforces students’ ability to classify triangles by consistently applying classification rules. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 11 | Math Example--Polygons--Triangle Classification: Example 11TopicTriangles DescriptionThis example shows a triangle with two sides labeled as x and a third side labeled y. Because two sides are congruent, the triangle is classified as isosceles. Triangles can be classified by their side lengths or angle measures. An isosceles triangle has two equal sides or angles, as seen in this example. Reviewing a series of examples helps students understand these classifications and recognize patterns in triangles. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 12 | Math Example--Polygons--Triangle Classification: Example 12TopicTriangles DescriptionThis example shows a triangle with side lengths all equal to 9. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be classified based on side or angle properties. An equilateral triangle has all sides and angles congruent. Viewing multiple examples reinforces students’ understanding of these classifications and enhances their ability to recognize triangle properties. Seeing several worked-out examples helps students understand and apply the rules consistently for classifying triangles. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 13 | Math Example--Polygons--Triangle Classification: Example 13TopicTriangles DescriptionThis example shows a triangle with three sides labeled as x, all equal in length. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be categorized by side length or angle measures. An equilateral triangle has all congruent sides and angles. Reviewing multiple examples helps students recognize triangle classifications by observing side and angle patterns. Providing several examples reinforces students’ ability to consistently classify triangles based on the observed properties. |
Definition of a Triangle |
|
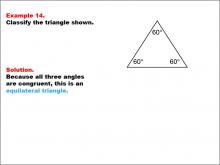
Math Example--Polygons--Triangle Classification: Example 14 | Math Example--Polygons--Triangle Classification: Example 14TopicTriangles DescriptionThis example shows a triangle with three angles, each measuring 60°. Since all angles are equal, the triangle is classified as equilateral. Triangle classification can be based on side lengths or angle measures. An equilateral triangle has all angles congruent. Reviewing examples like these helps students understand classification rules based on triangle properties. Multiple examples reinforce students' ability to identify triangle types consistently by observing angle or side characteristics. |
Definition of a Triangle |
|
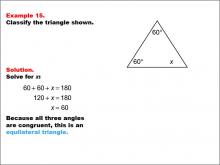
Math Example--Polygons--Triangle Classification: Example 15 | Math Example--Polygons--Triangle Classification: Example 15TopicTriangles DescriptionThis example presents a triangle with two angles labeled 60° and an unknown angle labeled x. Solving for x, we find it to be 60°, making all angles congruent and classifying the triangle as equilateral. Triangle classification can be determined by side length or angle measures. An equilateral triangle has all equal sides and angles. Observing multiple examples helps students apply these criteria consistently when classifying triangles. Seeing several worked examples helps students gain confidence in identifying triangles by recognizing congruent angles or sides. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 16 | Math Example--Polygons--Triangle Classification: Example 16TopicTriangles DescriptionThis example presents a triangle with three sides labeled as x, each equal in length. Since all three sides are congruent, the triangle is classified as equilateral. Triangles are categorized by their side lengths or angle measures. An equilateral triangle has all equal sides and angles, as seen in this example. Reviewing multiple examples reinforces students' understanding of the consistent characteristics that define each triangle type. Providing multiple worked-out examples helps students confidently apply classification rules to identify triangles by their properties. |
Definition of a Triangle |
|
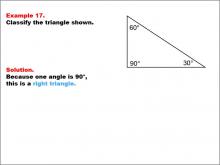
Math Example--Polygons--Triangle Classification: Example 17 | Math Example--Polygons--Triangle Classification: Example 17TopicTriangles DescriptionThis example shows a triangle with angles measuring 90°, 60°, and 30°. Since one angle is exactly 90°, the triangle is classified as a right triangle. Triangle classification often considers angle measures, with right triangles defined by having one 90° angle. Observing multiple examples allows students to consistently apply this classification rule. Reviewing various worked-out examples helps students solidify their understanding of identifying triangle types based on angle measurements. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 18 | Math Example--Polygons--Triangle Classification: Example 18TopicTriangles DescriptionThis example shows a triangle with two angles labeled 50° and 40° and an unknown angle x. Solving for x, we find it to be 90°, which classifies this as a right triangle. Triangles are classified by side lengths or angles, and a right triangle has a 90° angle. Examining examples like this helps students reinforce the criteria for identifying right triangles based on their angle properties. Seeing multiple worked-out examples enables students to apply classification rules more effectively and confidently. |
Definition of a Triangle |
|
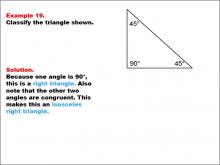
Math Example--Polygons--Triangle Classification: Example 19 | Math Example--Polygons--Triangle Classification: Example 19TopicTriangles DescriptionThis example presents a triangle with two congruent angles of 45° and one right angle of 90°. Because it has a 90° angle, the triangle is classified as a right triangle, and the two equal angles make it an isosceles right triangle. Triangle classification can involve side lengths or angles. A right triangle has a 90° angle, while isosceles triangles have two equal angles or sides. This example combines both classifications. Reviewing multiple examples helps students confidently apply the criteria to identify triangle types. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 2 | Math Example--Polygons--Triangle Classification: Example 2TopicTriangles DescriptionThis image shows a triangle with sides measuring 7, 8, and 9. The triangle is classified as scalene because each side has a different length, meaning no two sides are congruent. Triangles can be classified by examining their side lengths or angle measures. Scalene triangles, like the one shown, have no congruent sides, making them unique. This collection of examples helps students understand classification rules and visually identify different triangle types. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 20 | Math Example--Polygons--Triangle Classification: Example 20TopicTriangles DescriptionThis example shows a triangle with two known angles of 45° and an unknown angle x. Solving for x, we find it to be 90°, classifying this as a right triangle with two congruent angles, making it an isosceles right triangle. Triangle classification may be based on side lengths or angles. Right triangles have a 90° angle, while isosceles triangles have two equal sides or angles. Examples like this help students understand combined classifications. |
Definition of a Triangle |
|
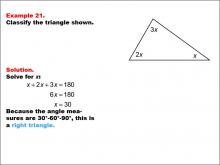
Math Example--Polygons--Triangle Classification: Example 21 | Math Example--Polygons--Triangle Classification: Example 21TopicTriangles DescriptionThis example shows a triangle with angles labeled as x, 2x, and 3x. Solving for x, we find that the angles are 30°, 60°, and 90°, classifying it as a right triangle. Triangle classification can involve angle measures or side lengths. Right triangles have one 90° angle, as seen here. Reviewing various examples supports students in consistently applying these classification rules. Observing multiple worked-out examples helps students gain confidence in identifying triangles based on the presence of specific angle measures. |
Definition of a Triangle |
|
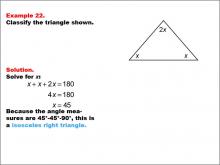
Math Example--Polygons--Triangle Classification: Example 22 | Math Example--Polygons--Triangle Classification: Example 22TopicTriangles DescriptionThis example shows a triangle with two equal angles labeled x and a third angle labeled 2x. Solving for x, we find the angles to be 45°, 45°, and 90°, classifying it as an isosceles right triangle. Triangles are classified by their angle measures or side lengths. Right triangles have a 90° angle, and isosceles triangles have two congruent angles. Reviewing examples like this one helps students understand combined classifications. |
Definition of a Triangle |
|
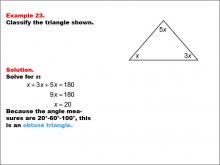
Math Example--Polygons--Triangle Classification: Example 23 | Math Example--Polygons--Triangle Classification: Example 23TopicTriangles DescriptionThis example shows a triangle with angles labeled x, 3x, and 5x. Solving for x, we find the angles to be 20°, 60°, and 100°, which classifies this triangle as obtuse because one of the angles is greater than 90°. Triangles can be classified by angle measures, with obtuse triangles defined as having one angle greater than 90°. Observing examples like this aids students in understanding how angle measures determine classifications. Providing multiple worked-out examples reinforces students' ability to consistently classify triangles based on angle properties. |
Definition of a Triangle |
|
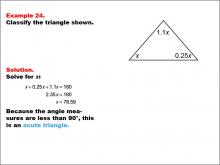
Math Example--Polygons--Triangle Classification: Example 24 | Math Example--Polygons--Triangle Classification: Example 24TopicTriangles DescriptionThis example shows a triangle with angles labeled as x, 0.25x, and 1.1x. Solving for x, we find that all angles are less than 90°, classifying the triangle as acute. Triangles are classified by their angle measures or side lengths, with acute triangles having all angles less than 90°. Reviewing examples like this helps students reinforce the criteria for classifying triangles based on angle sizes. Seeing multiple worked-out examples builds students' confidence in applying classification rules and identifying triangle types based on consistent properties. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 3 | Math Example--Polygons--Triangle Classification: Example 3TopicTriangles DescriptionThis example shows a triangle with side lengths of 12, 18, and x, where x is not equal to 12 or 18. The triangle is classified as scalene because all three side lengths are different. Triangles are categorized by side length or angle. Scalene triangles, with all sides unequal, demonstrate a key classification type. Multiple examples help students recognize classification patterns for triangles based on side length or angle measure. Observing various worked-out examples reinforces consistent application of classification criteria, building student confidence in identifying triangle types. |
Definition of a Triangle |
|
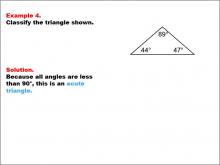
Math Example--Polygons--Triangle Classification: Example 4 | Math Example--Polygons--Triangle Classification: Example 4TopicTriangles DescriptionThis example displays a triangle with angles measuring 89°, 44°, and 47°. Since all angles are less than 90°, the triangle is classified as acute. Triangle classification can be based on side length or angle measures. Acute triangles have all angles less than 90°, as shown in this example. Reviewing multiple examples in this way helps students visually distinguish triangle types by angle. Providing varied worked-out examples solidifies students’ understanding of the criteria for each triangle type, enabling them to accurately identify triangles by their angle measures. |
Definition of a Triangle |
|
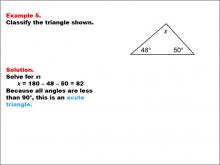
Math Example--Polygons--Triangle Classification: Example 5 | Math Example--Polygons--Triangle Classification: Example 5TopicTriangles DescriptionThis example presents a triangle with angles of 48°, 50°, and an unknown angle x. Solving for x, we find that x = 82°, meaning all angles are less than 90°, classifying it as acute. Triangles can be identified by their angles or side lengths. Acute triangles have all angles less than 90°, as seen here. Reviewing examples like this supports student understanding of angle-based classification. Seeing multiple worked examples helps students recognize patterns and confidently classify triangles based on established criteria. |
Definition of a Triangle |
|
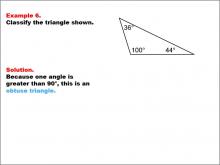
Math Example--Polygons--Triangle Classification: Example 6 | Math Example--Polygons--Triangle Classification: Example 6TopicTriangles DescriptionThis example shows a triangle with angles of 36°, 100°, and 44°. Because one of the angles is greater than 90°, this triangle is classified as obtuse. Triangles are classified by side lengths or angles. An obtuse triangle has one angle greater than 90°, as seen here. This collection of examples supports students in identifying and classifying triangles based on distinct angle measures. Seeing multiple worked-out examples reinforces students' understanding of classification rules, making it easier to recognize triangle types based on angle or side length. |
Definition of a Triangle |
|
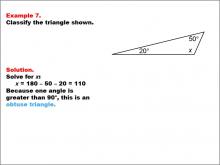
Math Example--Polygons--Triangle Classification: Example 7 | Math Example--Polygons--Triangle Classification: Example 7TopicTriangles DescriptionThis example presents a triangle with two known angles, 20° and 50°, and an unknown angle x. Solving for x, we find it to be 110°. Since one angle is greater than 90°, the triangle is classified as obtuse. Triangles can be classified by their angles, where obtuse triangles have one angle over 90°. Reviewing examples like this aids students in understanding classification based on angle measures. Seeing multiple examples reinforces the rules and helps students apply classification consistently and accurately. |
Definition of a Triangle |
|
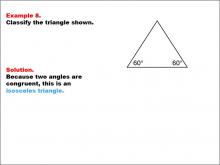
Math Example--Polygons--Triangle Classification: Example 8 | Math Example--Polygons--Triangle Classification: Example 8TopicTriangles DescriptionThis example shows a triangle with two angles, each measuring 60°. Since two angles are congruent, this triangle is classified as isosceles. Triangles can be categorized by side or angle properties. Isosceles triangles have two equal sides or two equal angles, as illustrated here. This collection of examples allows students to observe classifications and understand patterns in triangle properties. Examining multiple examples helps students confidently identify triangle types based on consistent characteristics. |
Definition of a Triangle |
|
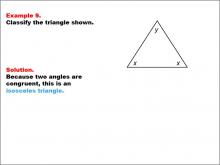
Math Example--Polygons--Triangle Classification: Example 9 | Math Example--Polygons--Triangle Classification: Example 9TopicTriangles DescriptionThis example shows a triangle with two angles labeled x and one angle labeled y. Since two angles are congruent, the triangle is classified as isosceles. Triangles can be classified by side lengths or angle measures. Isosceles triangles, with two equal sides or angles, are common. Observing various examples helps students understand these classification criteria. Providing multiple examples allows students to identify patterns in side and angle relationships, reinforcing accurate triangle classification. |
Definition of a Triangle |
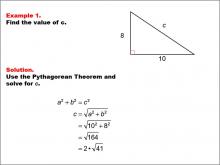
|
Math Example--Right Triangles-- Example 1 | Math Example--Right Triangles-- Example 1TopicRight Triangles DescriptionThis example presents a right triangle with sides of length 8 and 10, and an unknown hypotenuse labeled c. The task is to find the value of c using the Pythagorean Theorem. By applying the formula a2 + b2 = c2, we can calculate that c = √(102 + 82) = √(164) = 2 * √(41). |
Right Triangles |
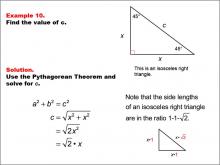
|
Math Example--Right Triangles-- Example 10 | Math Example--Right Triangles-- Example 10TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 11 | Math Example--Right Triangles-- Example 11TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 12 | Math Example--Right Triangles-- Example 12TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 13 | Math Example--Right Triangles-- Example 13TopicRight Triangles |
Right Triangles |
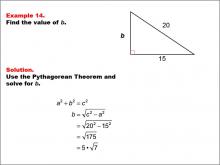
|
Math Example--Right Triangles-- Example 14 | Math Example--Right Triangles-- Example 14TopicRight Triangles |
Right Triangles |
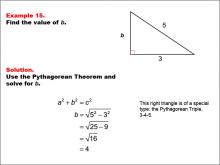
|
Math Example--Right Triangles-- Example 15 | Math Example--Right Triangles-- Example 15TopicRight Triangles |
Right Triangles |
|
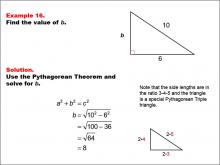
Math Example--Right Triangles-- Example 16 | Math Example--Right Triangles-- Example 16TopicRight Triangles |
Right Triangles |
|
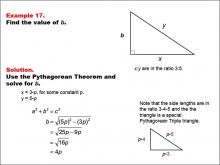
Math Example--Right Triangles-- Example 17 | Math Example--Right Triangles-- Example 17TopicRight Triangles |
Right Triangles |
|
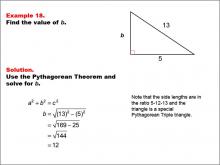
Math Example--Right Triangles-- Example 18 | Math Example--Right Triangles-- Example 18TopicRight Triangles |
Right Triangles |
|
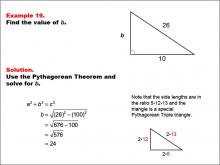
Math Example--Right Triangles-- Example 19 | Math Example--Right Triangles-- Example 19TopicRight Triangles |
Right Triangles |
|
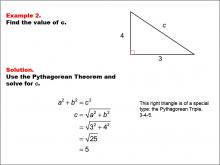
Math Example--Right Triangles-- Example 2 | Math Example--Right Triangles-- Example 2TopicRight Triangles DescriptionIn this example, we have a right triangle with sides of length 3 and 4, and an unknown hypotenuse labeled c. The goal is to determine the value of c using the Pythagorean Theorem. By applying the formula a2 + b2 = c2, we can calculate that c = √(32 + 42) = √(25) = 5. This example builds upon the previous one, reinforcing the application of the Pythagorean Theorem in right triangles. It demonstrates how the theorem can be used with different side lengths, helping students understand its versatility in solving various right triangle problems. |
Right Triangles |
|
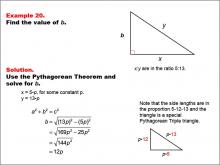
Math Example--Right Triangles-- Example 20 | Math Example--Right Triangles-- Example 20TopicRight Triangles |
Right Triangles |
|
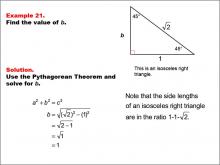
Math Example--Right Triangles-- Example 21 | Math Example--Right Triangles-- Example 21TopicRight Triangles |
Right Triangles |
|
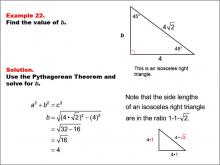
Math Example--Right Triangles-- Example 22 | Math Example--Right Triangles-- Example 22TopicRight Triangles |
Right Triangles |
|
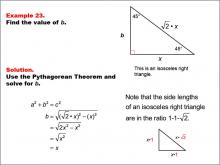
Math Example--Right Triangles-- Example 23 | Math Example--Right Triangles-- Example 23TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 24 | Math Example--Right Triangles-- Example 24TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 25 | Math Example--Right Triangles-- Example 25TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 26 | Math Example--Right Triangles-- Example 26TopicRight Triangles |
Right Triangles |
|
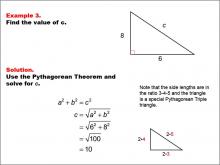
Math Example--Right Triangles-- Example 3 | Math Example--Right Triangles-- Example 3TopicRight Triangles |
Right Triangles |
|
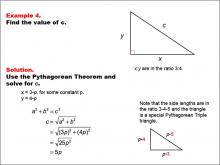
Math Example--Right Triangles-- Example 4 | Math Example--Right Triangles-- Example 4TopicRight Triangles |
Right Triangles |
|
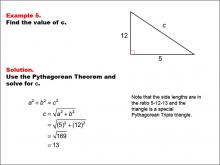
Math Example--Right Triangles-- Example 5 | Math Example--Right Triangles-- Example 5TopicRight Triangles |
Right Triangles |
|
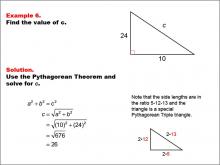
Math Example--Right Triangles-- Example 6 | Math Example--Right Triangles-- Example 6TopicRight Triangles |
Right Triangles |
|
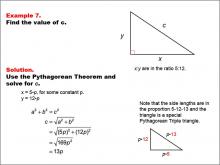
Math Example--Right Triangles-- Example 7 | Math Example--Right Triangles-- Example 7TopicRight Triangles |
Right Triangles |
|
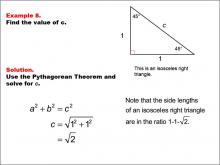
Math Example--Right Triangles-- Example 8 | Math Example--Right Triangles-- Example 8TopicRight Triangles |
Right Triangles |