Illustrative Math Alignment: Grade 8 Unit 9
Putting It All Together
Lesson 2: Regular Tessellations
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 10 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 10TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of x and θ. The solution involves using the central angle to find the fractional amount of the total area: A = (θ / 360) * π * x2 = πx2θ / 360. |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 11 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 11TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of x and θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * x) = (θ * x / 180) * π. |
Area and Circumference |
|
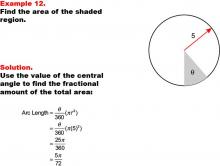
Math Example--Area and Perimeter--Circular Area and Circumference: Example 12 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 12TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the area of the shaded sector in terms of θ. The solution involves using the central angle to find the fractional amount of the total area: Area = (θ / 360) * (π * 52) = 25π / 360 * θ = 5π / 72 * θ. |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 13TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π. |
Area and Circumference |
|
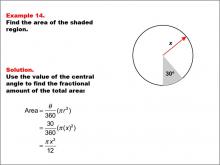
Math Example--Area and Perimeter--Circular Area and Circumference: Example 14 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 14TopicGeometry DescriptionThis example features a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded sector in terms of x. The solution involves using the central angle to find the fractional amount of the total area: Area = (30 / 360) * (π * x2) = π * x2 / 12. |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 15 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 15TopicGeometry DescriptionThis example presents a circle with radius x and a shaded sector with a central angle of 30 degrees. The task is to express the arc length of the shaded region in terms of x. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * (2 * π * x) = x / 6 * π. |
Area and Circumference |
|
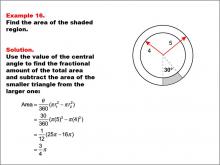
Math Example--Area and Perimeter--Circular Area and Circumference: Example 16 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 16TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded region. The solution involves using the central angle to determine the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * r12 - π * r22) = (30 / 360) * (π * 52 - π * 42) = π / 12 * (25 - 16) = 3π / 4. |
Area and Circumference |
|
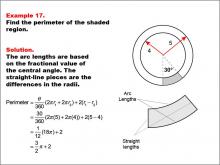
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 17TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2. |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 18 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 18TopicGeometry DescriptionThis example features two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x, y, and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * y2) = (θπ / 360) * (x2 - y2). |
Area and Circumference |
|
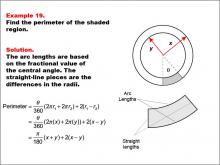
Math Example--Area and Perimeter--Circular Area and Circumference: Example 19 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 19TopicGeometry DescriptionThis example presents two concentric circles with radii x and y, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x, y, and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2πx + 2πy) + 2(x - y) = π/180 * θ(x + y) + 2(x - y). |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 2 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 2TopicGeometry DescriptionThis example features a circle with a radius of 5 units. The objective is to calculate the circumference of the circle using the given radius. The solution involves applying the circumference formula: C = 2 * π * r = 2 * π * (5) = 10π. Circular area and circumference calculations are fundamental in geometry. These examples provide students with practical applications of theoretical concepts, helping them understand the relationship between a circle's radius and its circumference. |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 20 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 20TopicGeometry DescriptionThis example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to express the area of the shaded region in terms of y. The solution involves calculating the difference between the areas of the larger and smaller circles, accounting for the central angle: Area = π/12 * (25 - y2). |
Area and Circumference |
|
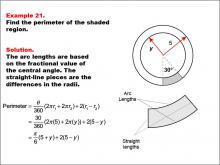
Math Example--Area and Perimeter--Circular Area and Circumference: Example 21 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 21TopicGeometry DescriptionThis example features two concentric circles with radii 5 and y, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. Given a central angle of 30 degrees, radius 5, and unknown radius y, the perimeter is calculated as: Perimeter = π/6 * (5 + y) + 2(5 - y). |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 22 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 22TopicGeometry DescriptionThis example presents two concentric circles with radii 4 and x, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * 42) = (θ * π / 360) * (x2 - 16). |
Area and Circumference |
|
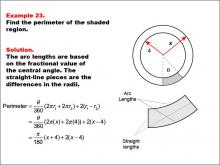
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 23TopicGeometry DescriptionThis example features two concentric circles with radii x and 4, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * x + 2 * π * 4) + 2 * (x - 4) = (π / 180) * θ(x + 4) + 2(x - 4). |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 3 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 3TopicGeometry DescriptionThis example introduces a circle with an unknown radius represented by x. The task is to express the area of the circle in terms of x. The solution demonstrates how to use the area formula with a variable radius: A = π * r2 = π * (x)2 = π * x2. Working with variable expressions in geometry helps students transition from concrete to abstract thinking. This example bridges the gap between numerical calculations and algebraic representations, a crucial skill in advanced mathematics. |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 4 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 4TopicGeometry DescriptionThis example presents a circle with an unknown radius represented by x. The task is to express the circumference of the circle in terms of x. The solution demonstrates how to use the circumference formula with a variable radius: C = 2 * π * r = 2 * π * x = 2πx. Understanding circular area and circumference is crucial in geometry. This example helps students transition from concrete numerical values to abstract algebraic expressions, fostering a deeper comprehension of the relationship between a circle's radius and its circumference. |
Area and Circumference |
|
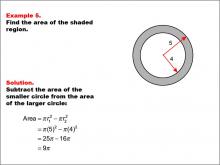
Math Example--Area and Perimeter--Circular Area and Circumference: Example 5 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 5TopicGeometry DescriptionThis example features two concentric circles with radii of 5 and 4 units. The task is to calculate the area of the shaded region between these circles. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * (4)2 = 25π - 16π = 9π. Concentric circles and shaded regions introduce students to more complex geometric concepts. This example builds upon basic circular area calculations, encouraging students to think about the relationships between different circles and how to find areas of composite shapes. |
Area and Circumference |
|
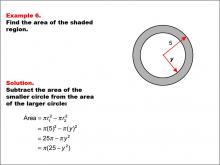
Math Example--Area and Perimeter--Circular Area and Circumference: Example 6 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 6TopicGeometry DescriptionThis example presents two concentric circles with radii of 5 and y units. The objective is to express the area of the shaded region between these circles in terms of y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * (5)2 - π * y2 = 25π - πy2 = π(25 - y2). |
Area and Circumference |
|
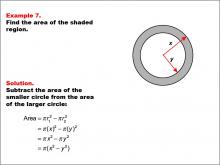
Math Example--Area and Perimeter--Circular Area and Circumference: Example 7 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 7TopicGeometry DescriptionThis example features two concentric circles with radii x and y. The task is to express the area of the shaded region between these circles in terms of x and y. The solution involves subtracting the area of the smaller circle from the area of the larger circle: A = π * x2 - π * y2 = π(x2 - y2). |
Area and Circumference |
|
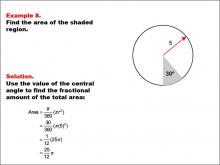
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 8TopicGeometry DescriptionThis example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12. |
Area and Circumference |
|
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9 | Math Example--Area and Perimeter--Circular Area and Circumference: Example 9TopicGeometry DescriptionThis example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6. |
Area and Circumference |
|
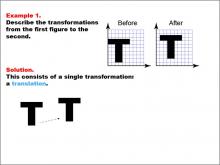
Math Example--Geometric Transformation--Transformations: Example 1 | Math Example--Geometric Transformation--Transformations: Example 1
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
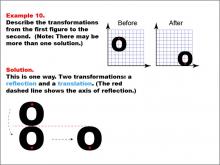
Math Example--Geometric Transformation--Transformations: Example 10 | Math Example--Geometric Transformation--Transformations: Example 10
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
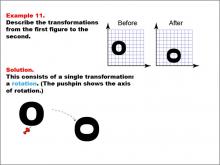
Math Example--Geometric Transformation--Transformations: Example 11 | Math Example--Geometric Transformation--Transformations: Example 11
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
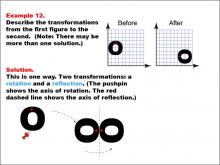
Math Example--Geometric Transformation--Transformations: Example 12 | Math Example--Geometric Transformation--Transformations: Example 12
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
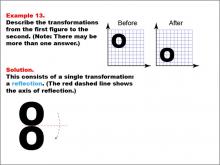
Math Example--Geometric Transformation--Transformations: Example 13 | Math Example--Geometric Transformation--Transformations: Example 13
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
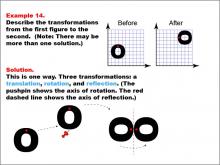
Math Example--Geometric Transformation--Transformations: Example 14 | Math Example--Geometric Transformation--Transformations: Example 14
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
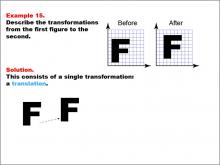
Math Example--Geometric Transformation--Transformations: Example 15 | Math Example--Geometric Transformation--Transformations: Example 15
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
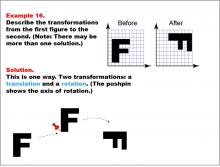
Math Example--Geometric Transformation--Transformations: Example 16 | Math Example--Geometric Transformation--Transformations: Example 16
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations: Example 17 | Math Example--Geometric Transformation--Transformations: Example 17
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
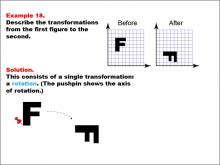
Math Example--Geometric Transformation--Transformations: Example 18 | Math Example--Geometric Transformation--Transformations: Example 18
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
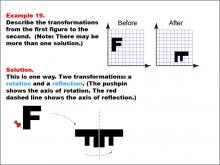
Math Example--Geometric Transformation--Transformations: Example 19 | Math Example--Geometric Transformation--Transformations: Example 19
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
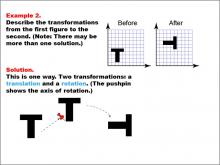
Math Example--Geometric Transformation--Transformations: Example 2 | Math Example--Geometric Transformation--Transformations: Example 2
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
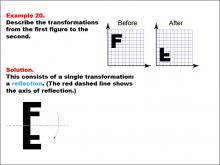
Math Example--Geometric Transformation--Transformations: Example 20 | Math Example--Geometric Transformation--Transformations: Example 20
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
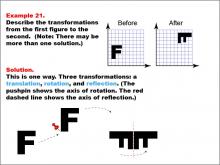
Math Example--Geometric Transformation--Transformations: Example 21 | Math Example--Geometric Transformation--Transformations: Example 21
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
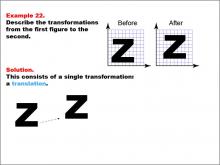
Math Example--Geometric Transformation--Transformations: Example 22 | Math Example--Geometric Transformation--Transformations: Example 22
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
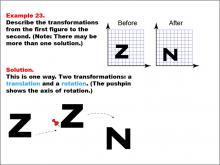
Math Example--Geometric Transformation--Transformations: Example 23 | Math Example--Geometric Transformation--Transformations: Example 23
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
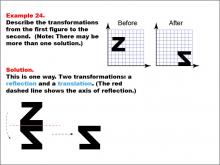
Math Example--Geometric Transformation--Transformations: Example 24 | Math Example--Geometric Transformation--Transformations: Example 24
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
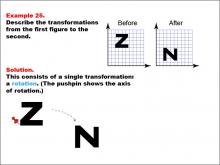
Math Example--Geometric Transformation--Transformations: Example 25 | Math Example--Geometric Transformation--Transformations: Example 25
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
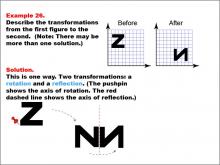
Math Example--Geometric Transformation--Transformations: Example 26 | Math Example--Geometric Transformation--Transformations: Example 26
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
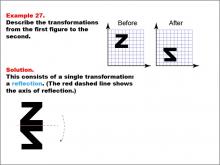
Math Example--Geometric Transformation--Transformations: Example 27 | Math Example--Geometric Transformation--Transformations: Example 27
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
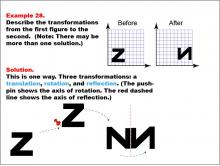
Math Example--Geometric Transformation--Transformations: Example 28 | Math Example--Geometric Transformation--Transformations: Example 28
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
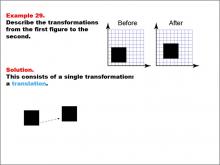
Math Example--Geometric Transformation--Transformations: Example 29 | Math Example--Geometric Transformation--Transformations: Example 29
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
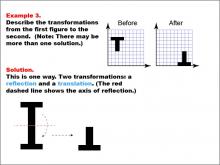
Math Example--Geometric Transformation--Transformations: Example 3 | Math Example--Geometric Transformation--Transformations: Example 3
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
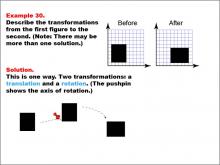
Math Example--Geometric Transformation--Transformations: Example 30 | Math Example--Geometric Transformation--Transformations: Example 30
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
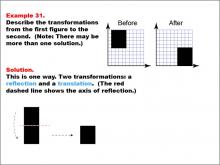
Math Example--Geometric Transformation--Transformations: Example 31 | Math Example--Geometric Transformation--Transformations: Example 31
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
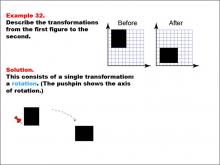
Math Example--Geometric Transformation--Transformations: Example 32 | Math Example--Geometric Transformation--Transformations: Example 32
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
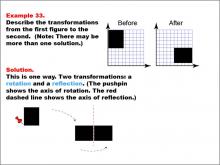
Math Example--Geometric Transformation--Transformations: Example 33 | Math Example--Geometric Transformation--Transformations: Example 33
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
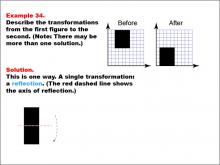
Math Example--Geometric Transformation--Transformations: Example 34 | Math Example--Geometric Transformation--Transformations: Example 34
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
