Illustrative Math Alignment: Grade 6 Unit 8

This is part of a collection of math worksheets on the topic of unit rates.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the topic of unit rates.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the topic of unit rates.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the topic of unit rates.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the topic of unit rates.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the topic of unit rates.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the topic of unit rates.

Related Resources

Worksheet Library

This is part of a collection of math worksheets on the topic of unit rates.

Related Resources

Worksheet Library

This is the transcript for the video of same title. Video contents: In this episode of Algebra Applications, students explore the dramatic events of 2008 related to the mortgage crisis. Brought about principally through mortgage defaults, the effect on the overall economy was severe. Yet, this situation offers an ideal case study for the exploration of key concepts in data analysis and probability. By exploring these questions students get a front row seat to the historical events of the world's largest economy.

This is the transcript for the video of same title. Video contents: In this introductory segment students learn about the mortage crisis of 2008. In the process they get a brief introduction to what a mortgage is.

To see the complete collection of video transcriptsy, click on this link.

This is the transcript for the video of same title. Video contents: The time value of money is at the basis of all loans. Students learn about the key factors that determine monthly mortgage payments and use the TI-Nspire to create an amortization table. This table is used throughout the rest of the program to explore different scenarios.

This is the transcript for the video of same title. Video contents: Having learned the general features of a mortgage, students learn the specifics of a subprime mortgage. With this comes the notion of a credit score, and with credit scores come the probabilities for a loan default. Students use the amortization table to run probability simulations to determine possible loan defaults on subprime mortgages.

This is the transcript for the video of same title. Video contents: Another factor in the mortgage crisis was the use of adjustable rate mortgages. Students run a number of scenarios to test adjustable rate mortgages, while also taking into account the state of the housing market during the time of the mortgage crisis.

This is the transcript for the video of same title. Video contents: What are the two meanings of statistics? What does it really mean that an event has a 50% probability of occurring? Why are data analysis and probability always taught together? Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video answers these questions and addresses fundamental concepts such as the law of large numbers and the notion of regression analysis. Both engaging investigations are based on true stories and real data, utilize different TI-Nspire iPad Applications, and model the seamless connection among various problem representations. Concepts explored: statistics, data analysis, regression analysis

This is the transcript for the video of same title. Video contents: In this Investigation we explore uncertainty and randomness.

To see the complete collection of video transcriptsy, click on this link.

This is the transcript for the video of same title. Video contents: In this Math Lab a hands-on probability activity involving coins is explored.

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of a set of numbers: 22, 13, 15, 1, 16, 28, 3, 5, 18, 42, 8, 9. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 41. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a set of numbers and find their difference. The process encourages critical thinking and helps students visualize the relationship between numbers in a dataset.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: -33, 38, 29, -8, 12, 2, 36, -8, 12, 18, -23, 50. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 83. This example is particularly useful as it includes both positive and negative numbers, helping students understand how to handle different types of values when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 16, 50, 24, 31, 30, 6, 22, 32, 43, 27, 48, 17, 36. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 44. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 34, 5, 43, 24, -48, -31, -49, 8, -41, 5, 0, 20, -41. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 92. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 49, 50, 18, 47, 29, 33, 27, 23, 34, 43, 17, 10, 15, 22. The solution involves arranging the numbers from least to greatest (10 to 50) and finding the difference between the two extremes. The range is calculated to be 40. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 0, 12, -41, -47, 7, -29, -34, -24, 38, 25, 23, -9, 38, 12. The solution involves arranging the numbers from least to greatest (-47 to 38) and finding the difference between the two extremes. The range is calculated to be 85. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 49, 20, 13, 40, 45, 14, 2, 27, 16, 48, 43, 39, 44, 26, 12. The solution involves arranging the numbers from least to greatest (2 to 49) and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

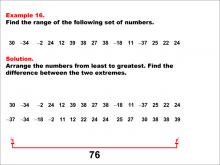
Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 30, -34, -2, 24, 12, 39, 38, 27, 38, -18, 11, -37, 25, 22, 24. The solution involves arranging the numbers from least to greatest (-37 to 39) and finding the difference between the two extremes. The range is calculated to be 76. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range.

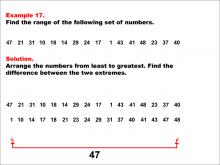
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 47, 21, 31, 10, 18, 14, 29, 24, 17, 1, 43, 41, 48, 23, 37, 40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: -2, -10, 24, -2, 26, 50, -40, 50, -40, 36, 30, -19, -40, 46, 27, -2. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 90. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 14, 29, 44, 37, 9, 6, 41, 30, 19, 2, 38, 50, 26, 24, 40, 11, 45. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 30, 31, -27, 46, 25, 6, 41, 1, -27, 40, -8, -35, 9, -25, -25, -41, -38. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 87. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

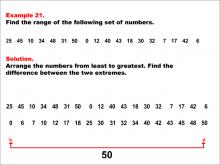
Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 25, 45, 10, 34, 48, 31, 50, 0, 12, 40, 43, 18, 30, 32, 7, 17, 42, 6. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 50. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

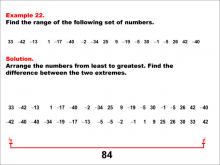
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 33, -42, -13, 1, -17, -40, -2, -34, 25, 9, -19, -5, 30, -1, -5, 26, 42, -40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 84. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

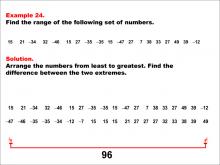
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 15, 21, -34, 32, -46, 15, 27, -35, -35, 15, -47, 27, 7, 38, 33, 27, 49, 39, -12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 96. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 42, 31, 16, 0, 35, 26, 30, 14, 6, 2, 13, 37, 33, 36, 19, 48, 3, 9, 45, 12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of non-negative numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 28, 49, 1, -19, -37, 43, 27, 32, -10, 39, -19, -48, -49, 28, 36, 37, 44, 42, 29, -17. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 98. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to calculate the mean of a dataset, a fundamental concept in statistics. The mean, often referred to as the average, is a measure of central tendency that provides insight into the typical value of a dataset. By visually presenting the calculation process, students can better grasp the concept and its application in real-world scenarios.

Topic

Measures of Central Tendency

Description

This example builds upon the concept of calculating the mean, introducing a slightly more complex dataset. It illustrates how the mean remains an effective measure of central tendency even as the numbers in the dataset become more varied. The visual representation helps students understand the step-by-step process of summing all values and dividing by the count of numbers.

Topic

Measures of Central Tendency

Description

This example further explores the concept of calculating the mean, introducing a dataset with a different range of values. It demonstrates how the mean can be used to find a central value even when the numbers in the dataset are more spread out. The visual representation continues to reinforce the process of summing all values and dividing by the count of numbers.

Topic

Measures of Central Tendency

Description

This example continues to reinforce the concept of calculating the mean, presenting a new set of numbers for analysis. It emphasizes the consistency of the process: summing all values and dividing by the count of numbers, regardless of the specific values in the dataset. The visual representation helps students see how different numbers can still lead to a single, representative value.

Topic

Measures of Central Tendency

Description

This fifth example in the series on calculating the mean introduces yet another set of numbers, further reinforcing the universality of the concept. It demonstrates how the process of finding the mean remains consistent: summing all values and dividing by the count of numbers, regardless of the specific values or the size of the dataset. The visual representation continues to aid in understanding the step-by-step process.

Topic

Measures of Central Tendency

Description

This sixth example in the series on calculating the mean introduces a new set of numbers, further solidifying the concept and its application. It reiterates the consistent process of finding the mean: summing all values and dividing by the count of numbers, regardless of the specific values in the dataset. The visual representation continues to support understanding of each step in the calculation.

Topic

Measures of Central Tendency

Description

This seventh example in the series on calculating the mean presents yet another set of numbers, further reinforcing the concept and its application in various scenarios. It continues to demonstrate the consistent process of finding the mean: summing all values and dividing by the count of numbers, regardless of the specific values or the size of the dataset. The visual representation aids in understanding each step of the calculation process.

Topic

Measures of Central Tendency

Description

This example demonstrates the calculation of the mean for a set of numbers: 2, 19, 7, 19, 16, 19, and 0. The process involves summing all values and dividing by the count of numbers, resulting in an average of approximately 11.71. This example reinforces the concept of finding a central value that represents the entire dataset.