
Illustrative Math Alignment: Grade 7 Unit 5
Rational Number Arithmetic
Lesson 8: Position, Speed, and Direction
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|
|
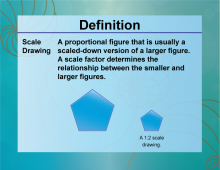
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor | Scale FactorTopicRatios, Proportions, and Percents DefinitionA scale factor is a number that scales, or multiplies, some quantity. DescriptionScale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Similar Figures | Similar FiguresTopicRatios, Proportions, and Percents DefinitionSimilar figures are figures that have the same shape but may differ in size; their corresponding angles are equal, and their corresponding sides are proportional. DescriptionSimilar figures are fundamental in geometry and are used in various real-world applications, such as creating scale models and maps. For example, two triangles are similar if their corresponding angles are equal and their sides are in proportion. This concept is essential for understanding geometric relationships and solving problems involving shapes and sizes. |
Proportions |
|
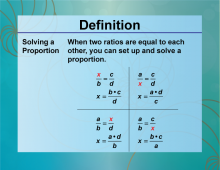
Definition--Ratios, Proportions, and Percents Concepts--Solving Proportions | Solving ProportionsTopicRatios, Proportions, and Percents DefinitionSolving proportions involves finding the value of a variable that makes two ratios equal. DescriptionSolving proportions is a key skill in algebra and is used in various applications, such as scaling recipes, converting units, and solving real-world problems. For example, if you know that 2/3 = x/6 you can solve for x by cross-multiplying to get 2 * 6 = 3 * x leading to x = 4 |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--The Constant of Proportionality | The Constant of ProportionalityTopicRatios, Proportions, and Percents DefinitionThe constant of proportionality is the constant value that relates two proportional quantities. DescriptionThe constant of proportionality is a fundamental concept in mathematics, particularly in linear relationships and direct variation. For example, in the equation y = kx, k is the constant of proportionality that relates y and x. This concept is crucial in fields like physics, where it is used to describe relationships such as speed (distance/time). |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--The Golden Ratio | The Golden RatioTopicRatios, Proportions, and Percents DefinitionThe Golden Ratio is a special number approximately equal to 1.618, often denoted by the Greek letter φ (phi), which appears in various aspects of art, architecture, and nature. |
Applications of Ratios, Proportions, and Percents and Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--The Percent One Number Is of Another | The Percent One Number Is of AnotherTopicRatios, Proportions, and Percents DefinitionThe percent one number is of another is a way to express one number as a percentage of another number. DescriptionUnderstanding how to express one number as a percentage of another is crucial in various real-world applications, such as calculating discounts, tax, and interest rates. For example, if you want to find out what percentage 25 is of 200, you divide 25 by 200 and multiply by 100, resulting in 12.5%. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Unit Rate | Unit RateTopicRatios, Proportions, and Percents DefinitionA unit rate is a comparison of any two separate but related measurements when one of the measurements is reduced to a single unit. DescriptionUnit rates are commonly used in everyday life, such as calculating speed (miles per hour), cost per item, or efficiency (miles per gallon). For example, if a car travels 300 miles on 10 gallons of gas, the unit rate is 30 miles per gallon. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Visual Models for Percents | Visual Models for PercentsTopicRatios, Proportions, and Percents DefinitionVisual models for percents are diagrams or illustrations that represent percentages to help visualize and understand them. DescriptionVisual models for percents are useful tools in various fields, such as education, finance, and statistics, to represent data and make it more comprehensible. For example, pie charts and bar graphs are common visual models that help illustrate percentages and proportions effectively. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Equivalent Ratios | Visualizing Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionVisualizing equivalent ratios involves using diagrams or models to show that two ratios are equivalent. DescriptionVisualizing equivalent ratios is important in fields such as mathematics and engineering, where understanding proportional relationships is crucial. For example, using a double number line or a ratio table can help illustrate that the ratios 2:3 and 4:6 are equivalent. |
Ratios and Rates |
|
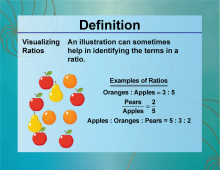
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Ratios | Visualizing RatiosTopicRatios, Proportions, and Percents DefinitionVisualizing ratios involves using diagrams or models to represent and understand the relationship between two quantities. DescriptionVisualizing ratios is essential in various fields, such as mathematics, science, and economics, where understanding the relationship between quantities is crucial. For example, using a bar model or a double number line can help illustrate the ratio of 3:4. |
Ratios and Rates |

|
Desmos Activity: Slope As Rate of Change | Desmos Activity: Slope As Rate of Change Use this activity to explore slope as a rate of change. In this Desmos activity, the slope of the line is the rate (cost per pound) for purchasing fruit. Students manipulate the slider for m to see the impact on the cost. |
Slope and Ratios and Rates |

|
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 1 | Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 1TopicGeometric Models |
Applications of Surface Area and Volume and Rational Functions and Equations |

|
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2 | Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2TopicGeometric Models |
Surface Area, Volume and Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Tutorial: Adding and Subtracting Rational Numbers | INSTRUCTIONAL RESOURCE: Tutorial: Adding and Subtracting Rational Numbers
In this Slide Show, learn how to add and subtract rational numbers. Includes links to several Media4Math videos and a math game. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Expressions and Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Why Are Wildfires So Dangerous? | INSTRUCTIONAL RESOURCE: Algebra Application: Why Are Wildfires So Dangerous?
In this Algebra Application, students learn about wildfires and the measurement of air quality. The math topics covered include: Scientific notation, Rates, Density, Data Analysis. The specific focus of this investigation is the health hazards from wildfire smoke. This includes a discussion of air density, measurement in microns, and measurement of air quality. Links to various web sites, including the EPA's site, provide relevant background information and data. The culminating activity is a case study of the wildfires in the Lake Tahoe area. Students analyze historical data and make a recommendation on the air quality. This is a great back-to-school activity for middle school or high school students. A relevant real-world application allows them to review math concepts. |
Laws of Exponents and Applications of Ratios, Proportions, and Percents |

|
INSTRUCTIONAL RESOURCE: Desmos Tutorial: Matching Coordinates to Rational Functions | INSTRUCTIONAL RESOURCE: Desmos Tutorial: Matching Coordinates to Rational Functions
In this Slide Show, use the Desmos graphing calculator to explore rational functions. To see the complete collection of Desmos Resources click on this link. Note: The download is a PPT file. This is part of a collection of Desmos tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Math Examples 23 | INSTRUCTIONAL RESOURCE: Math Examples--Graphs of Rational Functions
The complete set of 28 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Math Examples 44 | INSTRUCTIONAL RESOURCE: Math Examples--Rational Expressions
The complete set of 28 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Expressions and Rational Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Math Examples 45 | INSTRUCTIONAL RESOURCE: Math Examples--Rational Functions in Tabular and Graph Form
This set of tutorials provides 28 examples of rational functions in tabular and graph form. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Rational Expressions and Rational Functions and Equations |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 6)--Lesson 3--Solving Ratio and Rate Problems | Lesson Plan: Understanding Ratios and Rates This lesson introduces sixth-grade students to ratios and rates, emphasizing their applications in real-world problem-solving. Through hands-on activities, students will learn how to calculate unit rates, interpret proportional relationships, and analyze data using tables and graphs. |
Applications of Ratios, Proportions, and Percents |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 7)--Lesson 1--Introduction to Ratios and Unit Rates | Lesson Plan: Introduction to Ratios and Unit Rates This lesson introduces seventh-grade students to ratios and unit rates, emphasizing their real-world applications. Through engaging activities and problem-solving exercises, students will develop proportional reasoning skills. |
Ratios and Rates |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 7)--Lesson 2--Unit Rates and Complex Fractions | Lesson Plan: Unit Rates and Complex Fractions This lesson introduces seventh-grade students to unit rates and complex fractions, helping them develop a deeper understanding of proportional relationships and fraction operations. Students will learn to compute unit rates with fractional quantities, simplify complex fractions, and apply these skills to real-world situations such as speed calculations, recipe adjustments, and measurement conversions. |
Ratios and Rates and Applications of Ratios, Proportions, and Percents |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 7)--Lesson 5--Solving Multi-Step Ratio and Percent Problems | Lesson Plan: Solving Multi-Step Ratio Problems In this lesson, students will develop their problem-solving skills by tackling multi-step ratio and proportion problems. They will learn how to analyze complex ratio scenarios, apply proportional reasoning, and use unit conversions to solve real-world problems. This lesson builds on students' understanding of ratios and proportions, reinforcing their ability to work through multi-step calculations with confidence. Key concepts covered in this lesson include: |
Applications of Ratios, Proportions, and Percents |

|
Math Clip Art--Function Concepts--Graphs of Functions and Relations--Rational Function Graph | Math Clip Art--Function Concepts--Graphs of Functions and Relations--Rational Function GraphTopicFunctions DescriptionThis clip art depicts a rational function graph. Rational functions are quotients of polynomials and can have a wide variety of shapes depending on the degrees of the numerator and denominator. They generally pass the vertical line test and are thus functions, though they may have discontinuities. |
Rational Functions and Equations |

|
Math Clip Art: Slope vs. Rate | Math Clip Art: Slope vs. Rate In these clip art images, show students the difference between ratios and rates. These images are useful when talking about slope as both a ratio and a rate. In particular, this is useful when talking about slope as a rate of change. |
Slope and Ratios and Rates |
|
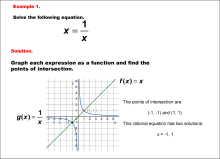
Math Example--Graphical Solutions to Rational Equations--Example 1 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
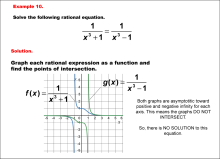
Math Example--Graphical Solutions to Rational Equations--Example 10 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
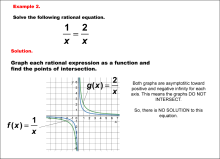
Math Example--Graphical Solutions to Rational Equations--Example 2 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
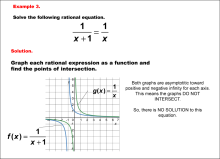
Math Example--Graphical Solutions to Rational Equations--Example 3 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
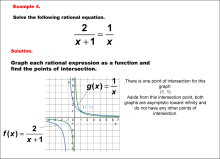
Math Example--Graphical Solutions to Rational Equations--Example 4 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
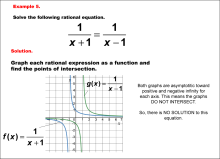
Math Example--Graphical Solutions to Rational Equations--Example 5 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
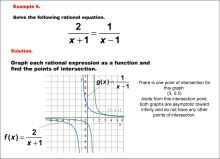
Math Example--Graphical Solutions to Rational Equations--Example 6 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
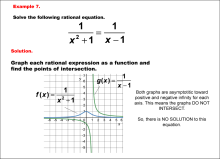
Math Example--Graphical Solutions to Rational Equations--Example 7 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
|
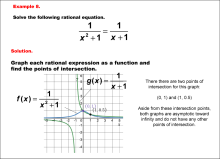
Math Example--Graphical Solutions to Rational Equations--Example 8 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
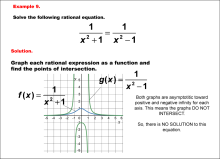
|
Math Example--Graphical Solutions to Rational Equations--Example 9 | This is part of a collection of math examples that show how to use graphical techniques to solve rational equations.
Note: The download is an image file.
Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Create a Slide ShowSubscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link:AccessibilityThis resource can also be used with a screen reader. |
Rational Functions and Equations |
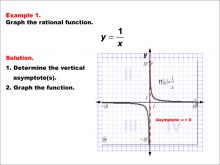
|
Math Example--Rational Concepts--Graphs of Rational Functions: Example 1 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 1TopicRational Functions DescriptionThis example demonstrates the graph of the rational function y = 1 / x. The graph is a hyperbola with vertical and horizontal asymptotes, with the vertical asymptote occurring at x = 0. Students are tasked with graphing the function and determining its vertical asymptote. |
Rational Functions and Equations |
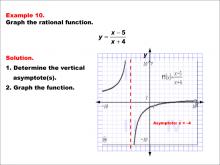
|
Math Example--Rational Concepts--Graphs of Rational Functions: Example 10 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 10TopicRational Functions DescriptionThis example showcases the graph of the rational function y = (x - 5) / (x + 4). The graph features a vertical asymptote at x = -4 and displays two branches, one in the first quadrant and one in the third quadrant. Students are asked to graph the function and identify its vertical asymptote. |
Rational Functions and Equations |
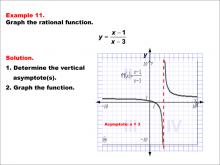
|
Math Example--Rational Concepts--Graphs of Rational Functions: Example 11 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 11TopicRational Functions DescriptionThis example showcases the graph of the rational function y = (x - 1) / (x - 3). The graph features a vertical asymptote at x = 3 and displays two distinct branches, one in the first quadrant and another in the third quadrant. Students are tasked with graphing the function and identifying its vertical asymptote. |
Rational Functions and Equations |
|
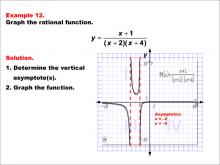
Math Example--Rational Concepts--Graphs of Rational Functions: Example 12 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 12TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = (x + 1) / ((x + 2)(x + 4)). The graph features two vertical asymptotes at x = -2 and x = -4, and displays three distinct branches, with one in each of the first, second, and third quadrants. Students are asked to graph the function and identify its vertical asymptotes. |
Rational Functions and Equations |
|
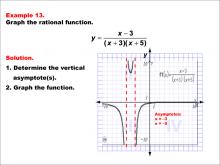
Math Example--Rational Concepts--Graphs of Rational Functions: Example 13 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 13TopicRational Functions DescriptionThis example presents the graph of the rational function y = (x - 3) / ((x + 3)(x + 5)). The graph features vertical asymptotes at x = -3 and x = -5, illustrating how the function behaves near these lines. Students are tasked with graphing the function and determining its vertical asymptotes. |
Rational Functions and Equations |
|
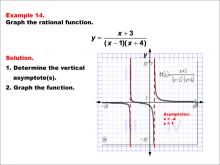
Math Example--Rational Concepts--Graphs of Rational Functions: Example 14 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 14TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = (x + 3) / ((x - 1)(x + 4)). The graph features vertical asymptotes at x = -4 and x = 1, displaying how the function behaves near these lines. Students are asked to graph the function and identify its vertical asymptotes. |
Rational Functions and Equations |
|
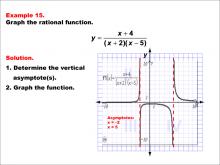
Math Example--Rational Concepts--Graphs of Rational Functions: Example 15 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 15TopicRational Functions DescriptionThis example showcases the graph of the rational function y = (x + 4) / ((x + 2)(x - 5)). The graph features vertical asymptotes at x = -2 and x = 5, demonstrating the behavior of the function near these asymptotes. Students are tasked with graphing the function and determining its vertical asymptotes. |
Rational Functions and Equations |
|
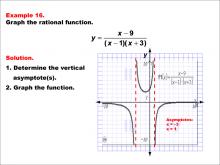
Math Example--Rational Concepts--Graphs of Rational Functions: Example 16 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 16TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = (x - 9) / ((x - 1)(x + 3)). The graph features vertical asymptotes at x = -3 and x = 1, showing the function's behavior around these asymptotes. Students are asked to graph the function and identify its vertical asymptotes. |
Rational Functions and Equations |
|
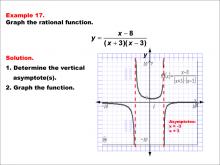
Math Example--Rational Concepts--Graphs of Rational Functions: Example 17 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 17TopicRational Functions DescriptionThis example presents the graph of the rational function y = (x - 1) / ((x - 2)(x - 3)). The graph features vertical asymptotes at x = 2 and x = 3, marked with dashed red lines. Students are tasked with graphing the function and determining its vertical asymptotes. |
Rational Functions and Equations |
|
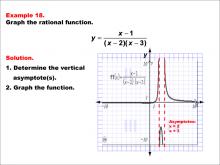
Math Example--Rational Concepts--Graphs of Rational Functions: Example 18 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 18TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = (x - 8) / ((x + 3)(x - 3)). The graph features vertical asymptotes at x = -3 and x = 3, highlighted by dashed red lines. Students are asked to graph the function and identify its vertical asymptotes. |
Rational Functions and Equations |
|
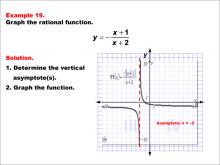
Math Example--Rational Concepts--Graphs of Rational Functions: Example 19 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 19TopicRational Functions DescriptionThis example presents the graph of the rational function y = -(x + 1) / (x + 2). The graph features a single vertical asymptote at x = -2, indicated by a dashed red line. Students are tasked with graphing the function and determining its vertical asymptote. |
Rational Functions and Equations |
|
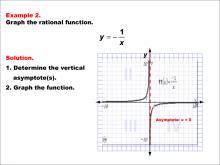
Math Example--Rational Concepts--Graphs of Rational Functions: Example 2 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 2TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = -1 / x. The graph is a hyperbola with vertical and horizontal asymptotes, with the vertical asymptote at x = 0. Students are asked to graph the function and identify its vertical asymptote. |
Rational Functions and Equations |
|
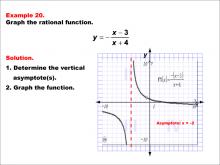
Math Example--Rational Concepts--Graphs of Rational Functions: Example 20 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 20TopicRational Functions DescriptionThis example showcases the graph of the rational function y = -(x - 3) / (x + 4). The graph features a vertical asymptote at x = -4, but it is incorrectly labeled as x = -2. Students are asked to graph the function and identify its vertical asymptote. |
Rational Functions and Equations |
|
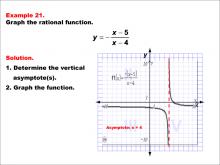
Math Example--Rational Concepts--Graphs of Rational Functions: Example 21 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 21TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = -(x - 5) / (x - 4). The graph features a vertical asymptote at x = 4, which is correctly labeled. Students are tasked with graphing the function and determining its vertical asymptote. |
Rational Functions and Equations |