
Illustrative Math Alignment: Grade 7 Unit 5
Rational Number Arithmetic
Lesson 8: Position, Speed, and Direction
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|
|
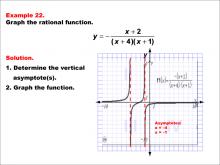
Math Example--Rational Concepts--Graphs of Rational Functions: Example 22 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 22TopicRational Functions DescriptionThis example presents the graph of the rational function y = -(x + 2) / ((x + 4)(x + 1)). The graph features vertical asymptotes at x = -4 and x = -1. Students are asked to graph the function and identify its vertical asymptotes. |
Rational Functions and Equations |
|
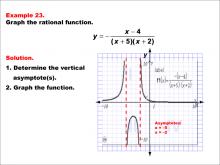
Math Example--Rational Concepts--Graphs of Rational Functions: Example 23 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 23TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = -(x - 4) / ((x + 5)(x + 2)). The graph features vertical asymptotes at x = -5 and x = -2. Students are tasked with graphing the function and determining its vertical asymptotes. |
Rational Functions and Equations |
|
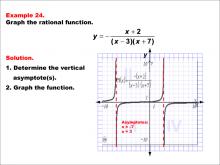
Math Example--Rational Concepts--Graphs of Rational Functions: Example 24 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 24TopicRational Functions DescriptionThis example showcases the graph of the rational function y = -(x + 2) / ((x - 3)(x + 7)). The graph features vertical asymptotes at x = -7 and x = 3. Students are asked to graph the function and identify its vertical asymptotes. |
Rational Functions and Equations |
|
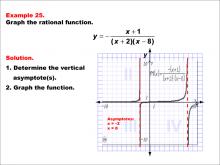
Math Example--Rational Concepts--Graphs of Rational Functions: Example 25 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 25TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = -(x + 1) / ((x + 2)(x - 8)). The graph features vertical asymptotes at x = -2 and x = 8. Students are tasked with graphing the function and determining its vertical asymptotes. |
Rational Functions and Equations |
|
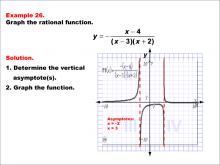
Math Example--Rational Concepts--Graphs of Rational Functions: Example 26 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 26TopicRational Functions DescriptionThis example showcases the graph of the rational function y = -(x - 4) / ((x - 3)(x + 2)). The graph features vertical asymptotes at x = -2 and x = 3. Students are asked to graph the function and identify its vertical asymptotes. |
Rational Functions and Equations |
|
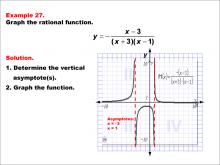
Math Example--Rational Concepts--Graphs of Rational Functions: Example 27 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 27TopicRational Functions DescriptionThis example presents the graph of the rational function y = -(x - 3) / ((x + 3)(x - 1)). The graph features vertical asymptotes at x = -3 and x = 1. Students are tasked with graphing the function and determining its vertical asymptotes. |
Rational Functions and Equations |
|
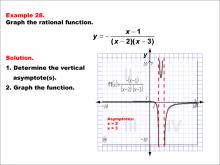
Math Example--Rational Concepts--Graphs of Rational Functions: Example 28 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 28TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = -(x - 1) / ((x - 2)(x - 3)). The graph features vertical asymptotes at x = 2 and x = 3, marked with dashed red lines on the coordinate plane. Students are asked to graph the function and identify its vertical asymptotes. |
Rational Functions and Equations |
|
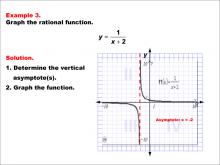
Math Example--Rational Concepts--Graphs of Rational Functions: Example 3 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 3TopicRational Functions DescriptionThis example showcases the graph of the rational function y = 1 / (x + 2). The graph is a hyperbola with a vertical asymptote at x = -2. Students are tasked with graphing the function and determining its vertical asymptote. |
Rational Functions and Equations |
|
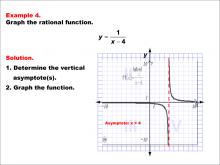
Math Example--Rational Concepts--Graphs of Rational Functions: Example 4 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 4TopicRational Functions DescriptionThis example presents the graph of the rational function y = 1 / (x - 4). The graph is a hyperbola with a vertical asymptote at x = 4. Students are asked to graph the function and identify its vertical asymptote. |
Rational Functions and Equations |
|
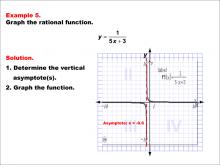
Math Example--Rational Concepts--Graphs of Rational Functions: Example 5 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 5TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = 1 / (5x + 3). The graph features a vertical asymptote at x = -0.6, indicated by a dashed red line. Students are tasked with graphing the function and determining its vertical asymptote. |
Rational Functions and Equations |
|
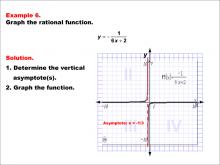
Math Example--Rational Concepts--Graphs of Rational Functions: Example 6 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 6TopicRational Functions DescriptionThis example demonstrates the graph of the rational function y = -1 / (6x + 2). The graph features a vertical asymptote at x = -1/3, shown with a dashed red line on the grid. Students are asked to graph the function and identify its vertical asymptote. |
Rational Functions and Equations |
|
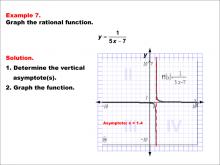
Math Example--Rational Concepts--Graphs of Rational Functions: Example 7 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 7TopicRational Functions DescriptionThis example showcases the graph of the rational function y = 1 / (5x - 7). The graph features a vertical asymptote at x = 1.4, marked by a dashed red line on the grid. Students are tasked with graphing the function and determining its vertical asymptote. |
Rational Functions and Equations |
|
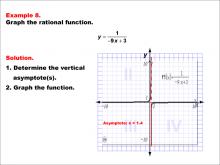
Math Example--Rational Concepts--Graphs of Rational Functions: Example 8 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 8TopicRational Functions DescriptionThis example presents the graph of the rational function y = 1 / (-9x + 3). The graph is plotted on a grid with a vertical asymptote at x = 1/3, marked by a dashed red line. Students are asked to graph the function and identify its vertical asymptote. |
Rational Functions and Equations |
|
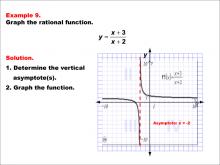
Math Example--Rational Concepts--Graphs of Rational Functions: Example 9 | Math Example--Rational Concepts--Graphs of Rational Functions: Example 9TopicRational Functions DescriptionThis example illustrates the graph of the rational function y = (x + 3) / (x + 2). The graph features a vertical asymptote at x = -2 and shows two branches, one in the second quadrant and one in the fourth quadrant. Students are tasked with graphing the function and determining its vertical asymptote. |
Rational Functions and Equations |
|
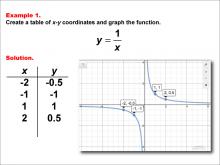
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 1 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 1TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / x. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph is a hyperbola with branches in the first and third quadrants, illustrating the characteristic shape of this basic rational function. |
Rational Functions and Equations |
|
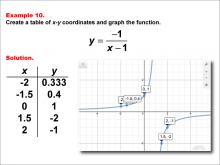
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 10 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 10TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = -1 / (x - 1). The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph includes labeled points at certain coordinates, illustrating how the negative sign in the numerator and the constant in the denominator affect the graph's shape and position. |
Rational Functions and Equations |
|
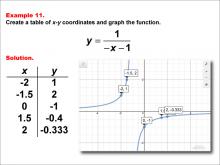
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 11 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 11TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x - 1). The image showcases both the table of x-y coordinates and the resulting graph. The graph is plotted with labeled points at given coordinates, illustrating how the negative sign and constant in the denominator affect the graph's shape and position. |
Rational Functions and Equations |
|
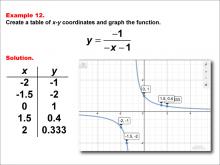
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 12 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 12TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x - 1). The image presents both the table of x-y coordinates and the resulting graph. The graph includes points labeled at specified coordinates, demonstrating how the negative signs in both the numerator and denominator, along with the constant, affect the graph's shape and position. |
Rational Functions and Equations |
|
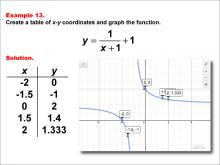
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 13 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 13TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (x + 1) + 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The table contains specific x-y coordinates: (-2, 0), (-1.5, -1), (0, 2), (1.5, 1.4), (2, 1.333), which are plotted on the graph. This example illustrates how adding a constant to a rational function affects its graph. |
Rational Functions and Equations |
|
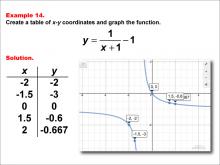
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 14 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 14TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (x + 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, -2), (-1.5, -3), (0, 0), (1.5, -0.6), (2, -0.667), which are plotted on the graph. This example illustrates how subtracting a constant from a rational function affects its graph. |
Rational Functions and Equations |
|
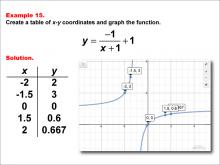
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 15 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 15TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (x + 1) + 1. The image presents both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, 2), (-1.5, 3), (0, 0), (1.5, 0.6), (2, 0.667), which are plotted on the graph. This example demonstrates how negating the numerator of a rational function and adding a constant affects its graph. |
Rational Functions and Equations |
|
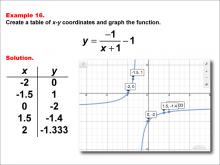
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 16 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 16TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = -1 / (x + 1) - 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The table contains specific x-y coordinates: (-2, 0), (-1.5, 1), (0, -2), (1.5, -1.4), (2, -1.333), which are plotted on the graph. This example illustrates how negating the numerator of a rational function and subtracting a constant affects its graph. |
Rational Functions and Equations |
|
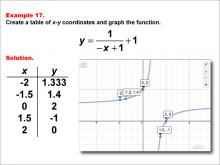
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 17 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 17TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x + 1) + 1. The image showcases both the table of x-y coordinates and the resulting graph. Points plotted include (-2, 1.333), (-1.5, 1.4), (0, 2), (1.5, -1), and (2, 0). The graph features a hyperbola with asymptotes, illustrating how negating the x-term in the denominator and adding a constant affects the graph's shape and position. |
Rational Functions and Equations |
|
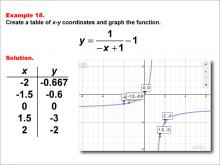
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 18 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 18TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x + 1) - 1. The image presents both the table of x-y coordinates and the resulting graph. Points plotted include (-2, -0.667), (-1.5, -0.6), (0, 0), (1.5, -3), and (2, -2). The graph shows a hyperbola with vertical and horizontal shifts, demonstrating how negating the x-term in the denominator and subtracting a constant affects the graph's shape and position. |
Rational Functions and Equations |
|
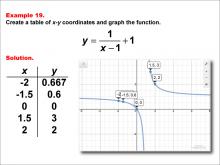
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 19 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 19TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (x - 1) + 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. Points include (-2, 0.667), (-1.5, 0.6), (0, 0), (1.5, 3), and (2, 2). The graph is a hyperbola with asymptotes at x = 1 and y = 1, illustrating how subtracting a constant in the denominator and adding a constant to the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
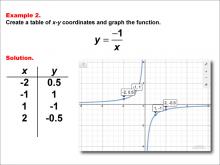
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 2 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 2TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / x. The image showcases both the table of x-y coordinates and the resulting graph. The graph is a hyperbola with branches in the second and fourth quadrants, illustrating how the negative sign affects the function's shape compared to the previous example. |
Rational Functions and Equations |
|
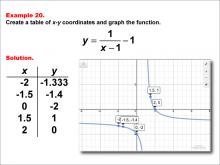
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 20 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 20TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (x - 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, -1.333), (-1.5, -1.4), (0, -2), (1.5, 1), and (2, 0). The graph is a hyperbola with shifted asymptotes at x = 1 and y = -1, illustrating how subtracting a constant in the denominator and from the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
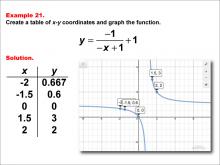
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 21 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 21TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = (-1) / (-x + 1) + 1. The image presents both the table of x-y coordinates and the resulting graph. It includes a table of x-y coordinates: (-2, 0.667), (-1.5, 0.6), (0, 0), (1.5, 3), and (2, 2). The graph is plotted on a grid, demonstrating how negating both the numerator and x-term in the denominator, while adding a constant to the entire fraction, affects the graph's shape and position. |
Rational Functions and Equations |
|
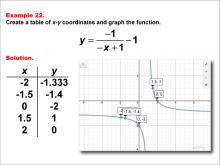
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 22 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 22TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = (-1) / (-x + 1) - 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. It includes a table of x-y coordinates: (-2, -1.333), (-1.5, -1.4), (0, -2), (1.5, 1), and (2, 0). The graph is plotted on a grid, illustrating how negating both the numerator and x-term in the denominator, while subtracting a constant from the entire fraction, affects the graph's shape and position. |
Rational Functions and Equations |
|
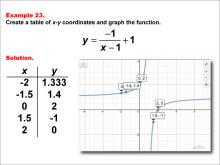
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 23 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 23TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = (-1) / (x - 1) + 1. The image shows both a table of x-y coordinates and the corresponding graph. The table includes points such as (-2, 1.333), (-1.5, 1.4), (0, 2), (1.5, -1), and (2, 0). The graph is plotted on a grid, illustrating how subtracting a constant in the denominator and adding a constant to the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
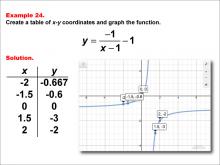
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 24 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 24TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = (-1) / (x - 1) - 1. The image shows both a table of x-y coordinates and the corresponding graph. The table includes points such as (-2, -0.667), (-1.5, -0.6), (0, 0), (1.5, -3), and (2, -2). The graph is plotted on a grid, illustrating how subtracting constants both in the denominator and from the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
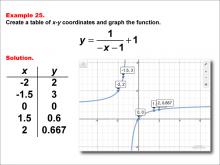
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 25 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 25TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x - 1) + 1. The image showcases both the table of x-y coordinates and the resulting graph. The graph shows points plotted at (-2, 2), (-1.5, 3), (0, 0), (1.5, 0.6), and (2, 0.667), illustrating how negating both terms inside the parentheses and adding a constant to the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |

|
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 26 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 26TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (-x - 1) - 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph shows points plotted at (-2, 0), (-1.5, 1), (0, -2), (1.5, -1.4), and (2, -1.333), illustrating how negating both terms inside the parentheses and subtracting a constant from the entire fraction affects the graph's shape and position. |
Rational Functions and Equations |
|
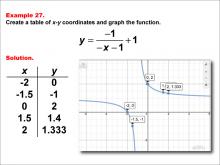
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 27 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 27TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x - 1) + 1. The image presents both the table of x-y coordinates and the resulting graph. The graph shows points plotted at (-2, 0), (-1.5, -1), (0, 2), (1.5, 1.4), and (2, 1.333), demonstrating how negating both the numerator and the terms inside the parentheses, while adding a constant to the entire fraction, affects the graph's shape and position. |
Rational Functions and Equations |
|
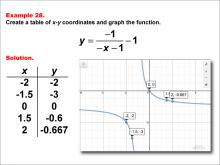
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 28 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 28TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x - 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The graph shows points plotted at (-2, -2), (-1.5, -3), (0, 0), (1.5, -0.6), and (2, -0.667), illustrating how negating both the numerator and the terms inside the parentheses, while subtracting a constant from the entire fraction, affects the graph's shape and position. |
Rational Functions and Equations |
|
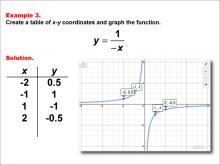
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 3 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 3TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x). The image presents both the table of x-y coordinates and the resulting graph. Interestingly, the graph is identical to that of y = -1 / x, showing a hyperbola with branches in the second and fourth quadrants. This example demonstrates how different forms of rational functions can produce the same graph. |
Rational Functions and Equations |

|
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 4 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 4TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x). The image showcases both the table of x-y coordinates and the resulting graph. Notably, the graph is identical to that of y = 1 / x, displaying a hyperbola with branches in the first and third quadrants. This example further illustrates how different forms of rational functions can produce the same graph. |
Rational Functions and Equations |

|
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 5 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 5TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (x + 1). The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph is a hyperbola with points marked at specific coordinates, illustrating how the addition of a constant in the denominator affects the graph's position. |
Rational Functions and Equations |

|
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 6 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 6TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (x + 1). The image showcases both the table of x-y coordinates and the resulting graph. The graph displays a hyperbola with labeled points on the curve, illustrating how the negative sign in the numerator and the constant in the denominator affect the graph's shape and position. |
Rational Functions and Equations |

|
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 7 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 7TopicRational Functions DescriptionThis math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (-x + 1). The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph is a hyperbola with specific points highlighted, illustrating how the negative sign and constant in the denominator affect the graph's shape and position. |
Rational Functions and Equations |
|
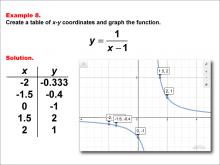
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 8 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 8TopicRational Functions DescriptionThis math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (x - 1). The image showcases both the table of x-y coordinates and the resulting graph. The graph features a hyperbola with marked points on its curve, illustrating how the constant in the denominator affects the graph's position. |
Rational Functions and Equations |

|
Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 9 | Math Example--Rational Concepts--Rational Functions in Tabular and Graph Form: Example 9TopicRational Functions DescriptionThis math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x + 1). The image presents both the table of x-y coordinates and the resulting graph. The graph is plotted with points labeled at specific coordinates, demonstrating how the negative signs in both the numerator and denominator affect the graph's shape and position. |
Rational Functions and Equations |
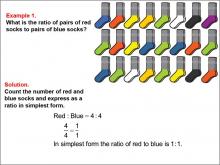
|
Math Example--Ratios and Rates--Example 1 | Math Example--Ratios and Rates--Example 1TopicRatios and Rates DescriptionThis math example focuses on understanding ratios using colored socks. The image displays a collection of red and blue socks, and students are asked to determine the ratio of red socks to blue socks. The solution demonstrates that there are 4 pairs of red socks and 4 pairs of blue socks, resulting in a ratio of 4 : 4, which simplifies to 1 : 1. |
Ratios and Rates |
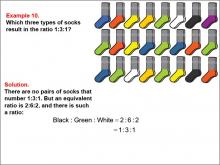
|
Math Example--Ratios and Rates--Example 10 | Math Example--Ratios and Rates--Example 10TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 3 : 1. |
Ratios and Rates |
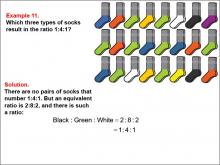
|
Math Example--Ratios and Rates--Example 11 | Math Example--Ratios and Rates--Example 11TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 4 : 1. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 12 | Math Example--Ratios and Rates--Example 12TopicRatios and Rates DescriptionThis example explores the concept of similar triangles using ratios. The image shows a right triangle with sides labeled as 9, 12, and 15 units. Students are asked to determine if this triangle is similar to a standard 3-4-5 Pythagorean triplet triangle. Understanding similar triangles is an important application of ratios in geometry. This example demonstrates how ratios can be used to compare the sides of triangles and determine similarity. By scaling the sides of a known triangle (3-4-5) and comparing them to the given triangle, students can see how ratios maintain proportionality in similar shapes. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 13 | Math Example--Ratios and Rates--Example 13TopicRatios and Rates DescriptionThis example focuses on verifying the similarity of triangles using ratios. The image shows a right triangle with sides labeled 25, 60, and 65 units. Students are guided through a step-by-step process to determine if this triangle is similar to a 5-12-13 right triangle. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 14 | Math Example--Ratios and Rates--Example 14TopicRatios and Rates DescriptionThis example explores the concept of special right triangles using ratios. The image shows a right triangle with sides labeled 3, 3 2 2 , and 6 units. Students are guided through a step-by-step process to verify if this triangle is similar to a 30°-60°-90° triangle. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 15 | Math Example--Ratios and Rates--Example 15TopicRatios and Rates |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 16 | Math Example--Ratios and Rates--Example 16TopicRatios and Rates DescriptionThis example focuses on converting units of speed and calculating rates. The image shows a car and calculations for converting speed from miles per hour to feet per second, given the distance traveled in miles and time in minutes. Understanding unit conversions and rate calculations is crucial in many real-world applications, particularly in physics and engineering. This example demonstrates how to use ratios to convert between different units of speed, showcasing the practical application of mathematical concepts in everyday scenarios. |
Ratios and Rates |