Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 19: Comparing Populations With Friends

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Definition--Measures of Central Tendency--Median of an Odd Data Set	Median of an Odd Data Set Topic Statistics Definition The median of an odd data set is one of the terms in the data set. Description The Median is the middle term of a data set. If the data set consists of an odd number of terms, no matter how many terms there are, the Median will be the middle term of that set. In mathematics education, understanding median of an odd data set is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Mode	Mode Topic Statistics Definition The mode is the most frequent data item.. Description The Mode is an important concept in statistics, used to summarize data effectively. It is the most frequent data item in a data set. A data set can have more than one mode. In mathematics education, understanding mode is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Mode of Categorical Data	Mode of Categorical Data Topic Statistics Definition The mode of categorical data is the most frequent item in a categorical data set. Description The Mode of Categorical Data is useful for finding the most frequent data item used with non-numerical data. For example, preferences for discrete characteristics can result in a mode.	Data Analysis
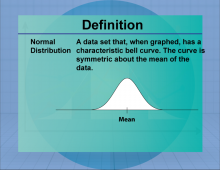
Definition--Measures of Central Tendency--Normal Distribution	Normal Distribution Topic Statistics Definition The normal distribution is a measure of central tendency that provides an average representation of a set of data. Description The Normal Distribution is an important concept in statistics, used to summarize data effectively. In real-world applications, the Normal Distribution helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research.	Data Analysis
Definition--Measures of Central Tendency--Outlier	Outlier Topic Statistics Definition The outlier is is an extreme value for a data set. Description The Outlier is an important concept in statistics. While it doesn't represent the average data set, it does set the range of extreme values in the data set. An outlier can be extremely large or small. In mathematics education, understanding outlier is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
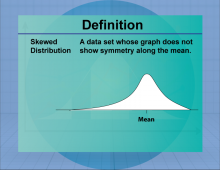
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Mean	Weighted Mean Topic Statistics Definition The weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. Description The weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Sequences and Series Concepts--Arithmetic Sequence	Arithmetic Sequence Topic Sequences and Series Definition An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. Description An arithmetic sequence is a fundamental concept in mathematics, particularly in the study of sequences and series. It is defined by the property that each term after the first is the sum of the previous term and a constant, known as the common difference. This concept is crucial in various mathematical applications, including solving problems related to linear growth and predicting future events based on past data.	Sequences
Definition--Sequences and Series Concepts--Arithmetic Series	Arithmetic Series Topic Sequences and Series Definition An arithmetic series is the sum of the terms of an arithmetic sequence. Description An arithmetic series is a significant concept in mathematics, especially in the study of sequences and series. It is formed by adding the terms of an arithmetic sequence. This concept is crucial for understanding how sums of linear patterns are calculated, which has applications in various fields such as finance, engineering, and computer science.	Series
Definition--Sequences and Series Concepts--Binomial Series	Binomial Series Topic Sequences and Series Definition The binomial series is the expansion of a binomial raised to any integer power. Description The binomial series is a powerful tool in mathematics, particularly in the study of sequences and series. It represents the expansion of a binomial expression raised to any integer power, which is essential in various mathematical and scientific applications, including probability, algebra, and calculus.	Series
Definition--Sequences and Series Concepts--Binomial Theorem	Binomial Theorem Topic Sequences and Series Definition The binomial theorem describes the algebraic expansion of powers of a binomial. Description The binomial theorem is a fundamental theorem in algebra that provides a formula for expanding binomials raised to any positive integer power. This theorem is essential in various mathematical disciplines, including algebra, calculus, and probability theory.	Series
Definition--Sequences and Series Concepts--Common Difference	Common Difference Topic Sequences and Series Definition The common difference is the difference between consecutive terms in an arithmetic sequence. Description The common difference is a key concept in arithmetic sequences, representing the consistent interval between consecutive terms. This concept is fundamental in understanding linear patterns and is widely used in various mathematical applications.	Sequences
Definition--Sequences and Series Concepts--Common Ratio	Common Ratio Topic Sequences and Series Definition The common ratio is the ratio between consecutive terms in a geometric sequence. Description The common ratio is a fundamental concept in geometric sequences, representing the consistent factor by which each term is multiplied to obtain the next term. This concept is crucial in understanding exponential growth and decay, which are prevalent in various mathematical and scientific applications.	Sequences
Definition--Sequences and Series Concepts--Convergent Series	Convergent Series Topic Sequences and Series Definition A convergent series is a series whose terms approach a specific value as the number of terms increases. Description A convergent series is a critical concept in the study of sequences and series, where the sum of its terms approaches a finite limit as the number of terms increases. This concept is essential in various mathematical and scientific applications, including calculus and analysis.	Series
Definition--Sequences and Series Concepts--Divergent Series	Divergent Series Topic Sequences and Series Definition A divergent series is a series whose terms do not approach a specific value as the number of terms increases. Description A divergent series is a significant concept in the study of sequences and series, where the sum of its terms does not approach a finite limit as the number of terms increases. This concept is essential in various mathematical and scientific applications, including calculus and analysis.	Series
Definition--Sequences and Series Concepts--Explicit Formula for a Sequence	Explicit Formula for a Sequence Topic Sequences and Series Definition An explicit formula for a sequence provides a direct way to calculate any term in the sequence. Description An explicit formula for a sequence is a mathematical expression that allows for the direct computation of any term in the sequence without needing to know the previous terms. This concept is fundamental in the study of sequences and series and is widely used in various mathematical applications.	Sequences
Definition--Sequences and Series Concepts--Fibonacci Sequence	Fibonacci Sequence Topic Sequences and Series Definition The Fibonacci sequence is a sequence where each term is the sum of the two preceding ones, starting from 0 and 1. Description The Fibonacci sequence is a famous sequence in mathematics, where each term is the sum of the two preceding ones, starting from 0 and 1. This sequence is significant in various mathematical and scientific applications, including computer science, biology, and art.	Sequences
Definition--Sequences and Series Concepts--Finite Sequence	Finite Sequence Topic Sequences and Series Definition A finite sequence is a sequence that has a limited number of terms. Description A finite sequence is a sequence with a specific number of terms, making it a crucial concept in the study of sequences and series. This concept is fundamental in various mathematical applications where the number of elements is limited, such as in statistics and computer science. In real-world applications, finite sequences are used in data analysis, where datasets have a specific number of entries. They are also used in computer algorithms that process a fixed number of elements. Algebraically, a finite sequence can be represented as	Sequences
Definition--Sequences and Series Concepts--Finite Series	Finite Series Topic Sequences and Series Definition A finite series is the sum of the terms of a finite sequence. Description A finite series is a significant concept in mathematics, representing the sum of the terms of a finite sequence. This concept is essential in various mathematical and scientific applications, including statistics, finance, and computer science. In real-world applications, finite series are used in financial calculations, such as determining the total amount of payments over a fixed period. They are also used in data analysis to find the sum of a dataset. Algebraically, a finite series can be expressed as	Series
Definition--Sequences and Series Concepts--Geometric Sequence	Geometric Sequence Topic Sequences and Series Definition A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. Description A geometric sequence is a fundamental concept in mathematics, particularly in the study of sequences and series. It is defined by the property that each term after the first is the product of the previous term and a constant, known as the common ratio. This concept is crucial in various mathematical applications, including exponential growth and decay.	Sequences
Definition--Sequences and Series Concepts--Geometric Series	Geometric Series Topic Sequences and Series Definition A geometric series is the sum of the terms of a geometric sequence. Description A geometric series is a significant concept in mathematics, especially in the study of sequences and series. It is formed by adding the terms of a geometric sequence. This concept is crucial for understanding how sums of exponential patterns are calculated, which has applications in various fields such as finance, engineering, and computer science.	Series
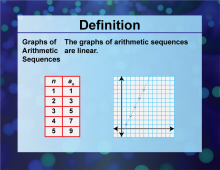
Definition--Sequences and Series Concepts--Graphs of Arithmetic Sequences	Graphs of Arithmetic Sequences Topic Sequences and Series Definition Graphs of arithmetic sequences form a linear graph on a coordinate plane. Description Graphs of arithmetic sequences are a visual tool used in mathematics to represent the terms of an arithmetic sequence on a coordinate plane. This concept is crucial for understanding linear patterns and relationships in sequences and series.	Sequences
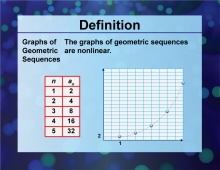
Definition--Sequences and Series Concepts--Graphs of Geometric Sequences	Graphs of Geometric Sequences Topic Sequences and Series Definition Graphs of geometric sequences visually represent the terms of a geometric sequence on a coordinate plane. These are nonlinear graphs. Description Graphs of geometric sequences are a visual tool used in mathematics to represent the terms of a geometric sequence on a coordinate plane. This concept is crucial for understanding exponential patterns and relationships in sequences and series.	Sequences
Definition--Sequences and Series Concepts--Infinite Sequence	Infinite Sequence Topic Sequences and Series Definition An infinite sequence is a sequence that continues indefinitely without terminating. Description An infinite sequence is a fundamental concept in mathematics, representing a sequence that continues indefinitely without terminating. This concept is essential in various mathematical and scientific applications, including calculus and analysis. In real-world applications, infinite sequences are used in mathematical modeling and simulations where processes continue indefinitely, such as in population dynamics or financial forecasting. Algebraically, an infinite sequence can be represented as	Sequences
Definition--Sequences and Series Concepts--Infinite Series	Infinite Series Topic Sequences and Series Definition An infinite series is the sum of the terms of an infinite sequence. Description An infinite series is a significant concept in mathematics, representing the sum of the terms of an infinite sequence. This concept is essential in various mathematical and scientific applications, including calculus and analysis. In real-world applications, infinite series are used in mathematical modeling and simulations where processes continue indefinitely, such as in signal processing or financial forecasting. Algebraically, an infinite series can be represented as	Series
Definition--Sequences and Series Concepts--Pascal's Triangle	Pascal's Triangle Topic Sequences and Series Definition Pascal's Triangle is a triangular array of binomial coefficients. Description Pascal's Triangle is a fundamental concept in mathematics, representing a triangular array of binomial coefficients. This concept is essential in various mathematical and scientific applications, including combinatorics, algebra, and probability theory. In real-world applications, Pascal's Triangle is used in probability calculations, particularly in binomial expansions and combinatorial problems. It is also used in computer science for algorithm design. Algebraically, the elements of Pascal's Triangle can be expressed as	Series
Definition--Sequences and Series Concepts--Recursive Formula	Recursive Formula Topic Sequences and Series Definition A recursive formula defines each term of a sequence using the preceding term(s). Description A recursive formula is a fundamental concept in mathematics, representing a way to define each term of a sequence using the preceding term(s). This concept is essential in various mathematical and scientific applications, including computer science and algorithm design.	Series
Definition--Sequences and Series Concepts--Sequences	Sequences Topic Sequences and Series Definition A sequence is an ordered list of numbers that follow a particular pattern or rule. Description Sequences are fundamental concepts in mathematics, representing ordered lists of numbers that follow a specific pattern or rule. This concept is crucial in various mathematical applications, including algebra, calculus, and computer science.	Sequences
Definition--Sequences and Series Concepts--Series	Series Topic Sequences and Series Definition A series is the sum of the terms of a sequence. Description Series are significant concepts in mathematics, representing the sum of the terms of a sequence. This concept is essential in various mathematical and scientific applications, including calculus, analysis, and financial modeling. In real-world applications, series are used in financial calculations, such as determining the total amount of payments or investments over time. They are also used in data analysis to find the sum of a dataset. Algebraically, series can be represented in various forms, such as arithmetic series, geometric series, and more.	Series
Definition--Sequences and Series Concepts--Square Numbers	Square Numbers Topic Sequences and Series Definition Square numbers are numbers that are the square of an integer. Description Square numbers are fundamental concepts in mathematics, representing numbers that are the square of an integer. This concept is crucial in various mathematical applications, including algebra, geometry, and number theory. In real-world applications, square numbers are used in area calculations, particularly in determining the area of squares. They are also used in computer algorithms and cryptography. Algebraically, square numbers can be represented as n2 , where n is an integer.	Sequences
Definition--Sequences and Series Concepts--Summation Notation	Summation Notation Topic Sequences and Series Definition Summation notation is a mathematical notation used to represent the sum of a sequence of terms. Description Summation notation is a powerful tool in mathematics, representing the sum of a sequence of terms in a compact form. This concept is essential in various mathematical and scientific applications, including calculus, statistics, and computer science.	Series
Definition--Sequences and Series Concepts--Triangular Numbers	Triangular Numbers Topic Sequences and Series Definition Triangular numbers are numbers that can be represented by an equilateral triangle. Description Triangular numbers are fundamental concepts in mathematics, representing numbers that can form an equilateral triangle. This concept is crucial in various mathematical applications, including algebra, geometry, and number theory. In real-world applications, triangular numbers are used in combinatorial problems and in determining the number of connections in a network. They are also used in computer algorithms and game design. Algebraically, triangular numbers can be represented as	Sequences
Definition--Statistics and Probability Concepts--Addition Rule of Probability	Addition Rule of Probability Topic Statistics and Probability Definition The Addition Rule of Probability is a key concept in statistics that helps in understanding the interaction between different events. Description The Addition Rule of Probability is crucial in the field of statistics because it allows us to make informed decisions based on the relationships between variables. For instance, in real-world applications, this concept is essential in various fields such as economics, social sciences, and health studies. Understanding how events affect each other can lead to better predictions and strategies.	Data Analysis
Definition--Statistics and Probability Concepts--Bivariate Data	Bivariate Data Topic Statistics and Probability Definition Bivariate data involves the analysis of two variables to determine relationships between them. Description Bivariate data is essential in statistics as it allows for the exploration of relationships between two variables, such as height and weight. This analysis is used in various fields, including economics, biology, and social sciences, to understand correlations and causations. For example, a scatter plot can be used to visually represent bivariate data, helping to identify trends or patterns.	Data Analysis
Definition--Statistics and Probability Concepts--Causation	Causation Topic Statistics and Probability Definition Causation refers to the relationship between two events where one event is affected by the other. Description Causation is a fundamental concept in statistics that distinguishes between correlation and causation. Understanding causation is vital in fields like medicine and social sciences to establish cause-effect relationships. For example, clinical trials are designed to establish causation between treatments and outcomes. Grasping causation is important for students to critically evaluate research findings and understand the implications of statistical analyses.	Data Analysis
Definition--Statistics and Probability Concepts--Combination 1	Combination 1 Topic Statistics and Probability Definition A combination is a selection of items from a larger pool where order does not matter. Description Combinations are used in probability to determine the number of ways to select items from a set, which is crucial in fields like cryptography and game theory. The formula for combinations is where n is the total number of items, and r is the number of items to choose.	Data Analysis
Definition--Statistics and Probability Concepts--Combination 2	Combination 2 Topic Statistics and Probability Definition A combination is a selection of items from a larger pool where order does not matter. Description Combinations are used in probability to determine the number of ways to select items from a set, which is crucial in fields like cryptography and game theory. The formula for combinations is where n is the total number of items, and r is the number of items to choose.	Probability
Definition--Statistics and Probability Concepts--Compound Events	Compound Events Topic Statistics and Probability Definition A compound event in probability is an event that consists of two or more simple events. Description Compound events are important in probability as they allow for the calculation of the likelihood of multiple events occurring together, which is applicable in areas like risk assessment and decision-making. Understanding compound events helps students develop skills to analyze complex scenarios and calculate probabilities effectively.	Probability
Definition--Statistics and Probability Concepts--Conditional Probability	Conditional Probability Topic Statistics and Probability Definition Conditional probability is the probability of an event occurring given that another event has already occurred. Description Conditional probability is used in statistics to refine predictions and is essential in fields like epidemiology and finance. For example, the probability of drawing a red card given that is a face card is drawn is a conditional probability. Understanding conditional probability is crucial for students to analyze dependent events and make informed predictions.	Data Analysis
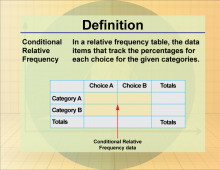
Definition--Statistics and Probability Concepts--Conditional Relative Frequency	Conditional Relative Frequency Topic Statistics and Probability Definition Conditional relative frequency is the ratio of the frequency of a subset of data to the frequency of a condition. Description Conditional relative frequency is crucial in analyzing categorical data, helping to understand the distribution of data under specific conditions. For example, the frequency of students who pass a test given they have attended all classes is a conditional relative frequency. Understanding this concept helps students interpret data in surveys and experiments more accurately.	Data Analysis