Illustrative Math Alignment: Grade 7 Unit 8

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image shows a math example about finding the mode of a set of numbers. The numbers are arranged from least to greatest with the mode highlighted. This demonstrates how to identify the mode when a number appears more frequently than others in a data set.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image shows a math example about finding the mode of a set of numbers. The numbers are arranged from least to greatest with the modes highlighted. This demonstrates that a data set can have multiple modes, which occurs when two or more numbers appear with the highest frequency.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image shows a math example about finding the mode of a set of numbers. The numbers are arranged from least to greatest and it is determined that there is no mode. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows a math example focusing on finding the mode of a set of numbers. The numbers are arranged in ascending order to identify the mode. Highlighted numbers indicate the mode. This demonstrates how to identify the mode when a number appears more frequently than others in a data set that includes both positive and negative numbers.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image presents a math example about finding the mode. The numbers are sorted in ascending order with highlighted sections showing the modes. This demonstrates that a data set can have multiple modes, even when it contains both positive and negative numbers.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. A math example illustrating how to find the mode of a number set is presented. The numbers are ordered from least to greatest and it concludes that there is no mode. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. This image provides an example of finding the mode in a data set. Numbers are arranged in ascending order and highlighted to show which number appears most frequently. This demonstrates how to identify the mode when a number appears more frequently than others in a data set.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows a math problem about finding the mode of a set of numbers. It includes the original set of numbers and the same set arranged in ascending order with the mode highlighted. This demonstrates that a data set can have multiple modes, which occurs when two or more numbers appear with the highest frequency.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image presents a math problem about finding the mode of a set of numbers. It shows the original set and the same set arranged in ascending order. The solution states "No Mode". This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image displays a math problem about finding the mode of a set of numbers. It includes the original set of numbers and the same set arranged in ascending order with the mode highlighted. This demonstrates how to identify the mode when a number appears more frequently than others in a data set that includes both positive and negative numbers.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 6 displays a mix of negative and positive numbers with two modes highlighted. The example illustrates that a data set can have multiple modes, even when it contains both positive and negative numbers. In this case, -37 and 19 are identified as the modes.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows a math problem about finding the mode of a set of numbers. It includes the original set of numbers and the same set arranged in ascending order with two potential modes highlighted. This demonstrates that a data set can have multiple modes, even when it contains both positive and negative numbers.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows Example 61, which involves finding the mode of a set of numbers. The numbers are listed, and then arranged from least to greatest. It concludes with "No Mode." This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows Example 62 with a list of numbers. After sorting them in ascending order, it identifies the mode as "20." This demonstrates how to identify the mode when a number appears more frequently than others in a data set.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows Example 63 with a list of numbers. After sorting them in ascending order, it identifies two modes: "20" and "44." This demonstrates that a data set can have multiple modes, which occurs when two or more numbers appear with the highest frequency.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows Example 64 with a list of numbers. After sorting them in ascending order without any repetition in frequency higher than others, it concludes with "No Mode." This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 65 shows a list of numbers with the mode highlighted. The numbers are arranged in ascending order. This demonstrates how to identify the mode when a number appears more frequently than others in a data set that includes both positive and negative numbers.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 66 displays a set of numbers with two modes highlighted. The numbers are sorted in ascending order. This demonstrates that a data set can have multiple modes, even when it contains both positive and negative numbers.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 67 presents a list of numbers with no mode indicated. The numbers are sorted in ascending order. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 68 illustrates a set of numbers with the mode highlighted. The numbers are arranged in ascending order. This demonstrates how to identify the mode when a number appears more frequently than others in a data set.

Topic

Measures of Central Tendency

Description

This example showcases a situation where there are multiple modes in a dataset. The image shows how numbers are arranged from least to greatest and highlights two modes: "26" and "36." This demonstrates that datasets can have more than one mode when two or more numbers appear with equal highest frequency.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 7 presents a set of numbers with no repeating values; no mode is found. This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Description

The image presents a math example on determining the mode of a sequence of numbers. After sorting them in order from least to greatest, the number -7 is highlighted as it appears most frequently. This demonstrates how to identify the mode when a number appears more frequently than others in a data set that includes both positive and negative numbers.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

This image shows a math example on finding the mode in a data set. The numbers are sorted from least to greatest with two modes highlighted: 15 and 27. This demonstrates that a data set can have multiple modes, which occurs when two or more numbers appear with the highest frequency.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

The image shows a math problem about finding the mode of a set of numbers. It includes the original set of numbers and the same set arranged in ascending order. The solution indicates "No Mode". This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

The image presents a math problem about finding the mode of a set of numbers. It shows the original set and the same set arranged in ascending order. The solution highlights the number 27 as occurring most frequently. This demonstrates how to identify the mode when a number appears more frequently than others in a data set.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

The image displays a math problem about finding the mode of a set of numbers. It includes the original set and the same set arranged in ascending order. The solution highlights two numbers, 24 and 34, as occurring most frequently. This demonstrates that a data set can have multiple modes, which occurs when two or more numbers appear with the highest frequency.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

The image shows a math problem about finding the mode of a set of numbers. It presents the original set and the same set arranged in ascending order. The solution indicates "No Mode". This example reinforces the concept that not all data sets have a mode, particularly when each number in the set appears only once.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

The image shows a math example focused on finding the mode of a set of numbers. The numbers are initially listed in random order and then rearranged from least to greatest. The mode is highlighted. This demonstrates how to identify the mode when a number appears more frequently than others in a data set that includes both positive and negative numbers.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

The image depicts another math example on finding the mode. It includes a list of numbers that are sorted from least to greatest. The mode is identified and highlighted in red. This demonstrates how to identify multiple modes when two or more numbers appear with equal highest frequency in a data set.

Lessons on measures of central tendency help students understand how to interpret data using different statistical measures like mean and median along with mode.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. Example 8 includes a set of numbers with one mode highlighted. The numbers are sorted in ascending order, revealing that 8 appears twice, while all other numbers appear only once. This demonstrates how to identify the mode when one number occurs more frequently than others in a data set.

Topic

Measures of Central Tendency

Description

This example showcases a situation of measures of central tendency, where the goal is to identify a key summary measure in a set of data. The image shows an example of finding the mode from a set of numbers. The numbers are arranged from least to greatest, highlighting the most frequent ones. After sorting, it becomes clear that both 9 and 43 appear twice, while all other numbers appear only once. This example demonstrates that a data set can have more than one mode.

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: -33, 38, 29, -8, 12, 2, 36, -8, 12, 18, -23, 50. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 83. This example is particularly useful as it includes both positive and negative numbers, helping students understand how to handle different types of values when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 16, 50, 24, 31, 30, 6, 22, 32, 43, 27, 48, 17, 36. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 44. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 34, 5, 43, 24, -48, -31, -49, 8, -41, 5, 0, 20, -41. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 92. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 49, 50, 18, 47, 29, 33, 27, 23, 34, 43, 17, 10, 15, 22. The solution involves arranging the numbers from least to greatest (10 to 50) and finding the difference between the two extremes. The range is calculated to be 40. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 0, 12, -41, -47, 7, -29, -34, -24, 38, 25, 23, -9, 38, 12. The solution involves arranging the numbers from least to greatest (-47 to 38) and finding the difference between the two extremes. The range is calculated to be 85. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 49, 20, 13, 40, 45, 14, 2, 27, 16, 48, 43, 39, 44, 26, 12. The solution involves arranging the numbers from least to greatest (2 to 49) and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference.

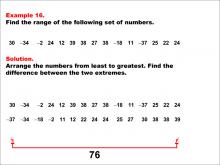
Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 30, -34, -2, 24, 12, 39, 38, 27, 38, -18, 11, -37, 25, 22, 24. The solution involves arranging the numbers from least to greatest (-37 to 39) and finding the difference between the two extremes. The range is calculated to be 76. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range.

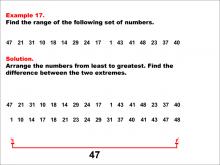
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 47, 21, 31, 10, 18, 14, 29, 24, 17, 1, 43, 41, 48, 23, 37, 40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: -2, -10, 24, -2, 26, 50, -40, 50, -40, 36, 30, -19, -40, 46, 27, -2. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 90. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 14, 29, 44, 37, 9, 6, 41, 30, 19, 2, 38, 50, 26, 24, 40, 11, 45. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

Topic

Measures of Central Tendency

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 30, 31, -27, 46, 25, 6, 41, 1, -27, 40, -8, -35, 9, -25, -25, -41, -38. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 87. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.

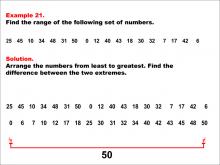
Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 25, 45, 10, 34, 48, 31, 50, 0, 12, 40, 43, 18, 30, 32, 7, 17, 42, 6. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 50. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

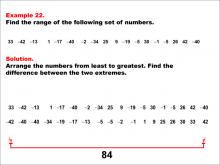
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 33, -42, -13, 1, -17, -40, -2, -34, 25, 9, -19, -5, 30, -1, -5, 26, 42, -40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 84. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range.

Topic

Measures of Central Tendency

Description

This example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference.

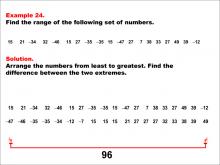
Topic

Measures of Central Tendency

Description

This example illustrates how to find the range of the following set of numbers: 15, 21, -34, 32, -46, 15, 27, -35, -35, 15, -47, 27, 7, 38, 33, 27, 49, 39, -12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 96. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range.