Illustrative Math Alignment: Grade 7 Unit 8

Probability and Sampling

Lesson 20: Memory Test

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Closed Captioned Video: Ratios: Ratios with Three Items	Closed Captioned Video: Ratios: Ratios with Three Items What Are Ratios? A ratio is the relationship between two or more quantities among a group of items.	Ratios and Rates
Closed Captioned Video: Ratios: Unit Rates	Closed Captioned Video: Ratios: Unit Rates What Are Ratios? A ratio is the relationship between two or more quantities among a group of items.	Ratios and Rates
Closed Captioned Video: Ratios: Visual Models for Ratios	Closed Captioned Video: Ratios: Visual Models for Ratios What Are Ratios? A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.	Ratios and Rates
Closed Captioned Video: Ratios: Visual Models for Ratios and Percents	Closed Captioned Video: Ratios: Visual Models for Ratios and Percents What Are Ratios? A ratio is the relationship between two or more quantities among a group of items.	Ratios and Rates
Closed Captioned Video: Ratios: What Are Ratios?	Closed Captioned Video: Ratios: What Are Ratios? What Are Ratios? A ratio is the relationship between two or more quantities among a group of items.	Ratios and Rates
Definition--Charts and Graphs--Bar Graph	Definition--Charts and Graphs--Bar Graph This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
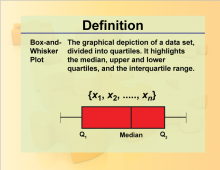
Definition--Charts and Graphs--Box-and-Whisker Plot	Definition--Charts and Graphs--Box-and-Whisker Plot This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Categorical Data	Definition--Charts and Graphs--Categorical Data This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Circle Graph	Definition--Charts and Graphs--Circle Graph This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Continuous Data	Definition--Charts and Graphs--Continuous Data This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Discrete Data	Definition--Charts and Graphs--Discrete Data This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Frequency Table	Definition--Charts and Graphs--Frequency Table This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
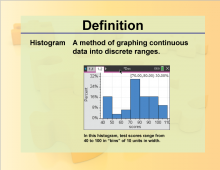
Definition--Charts and Graphs--Histogram	Definition--Charts and Graphs--Histogram This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
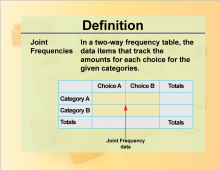
Definition--Charts and Graphs--Joint Frequencies	Definition--Charts and Graphs--Joint Frequencies This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
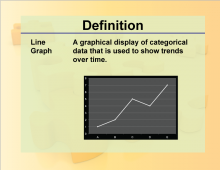
Definition--Charts and Graphs--Line Graph	Definition--Charts and Graphs--Line Graph This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Line Plot	Definition--Charts and Graphs--Line Plot This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Pictograph	Definition--Charts and Graphs--Pictograph This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Scaled Pictograph	Definition--Charts and Graphs--Scaled Pictograph This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
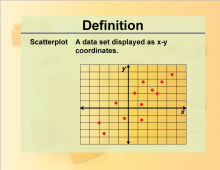
Definition--Charts and Graphs--Scatterplot	Definition--Charts and Graphs--Scatterplot This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Stem-and-Leaf Plot	Definition--Charts and Graphs--Stem-and-Leaf Plot This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Charts and Graphs--Two-Way Frequency Table	Definition--Charts and Graphs--Two-Way Frequency Table This is a collection of definitions related to the concept of charts, graphs, and data displays.	Data Analysis
Definition--Complex Fraction	Complex Fraction Topic Fractions Definition A complex fraction is a fraction where the numerator, the denominator, or both, contain a fraction themselves. Description Complex fractions are an important concept in the study of fractions and algebra. They appear in various mathematical contexts, particularly when dealing with rational expressions and advanced algebraic operations. Understanding complex fractions is essential for simplifying expressions and solving equations that involve multiple layers of fractions.	Fractions and Mixed Numbers
Definition--Measures of Central Tendency	Measures of Central Tendency Topic Statistics Definition The measures of central tendency is a measure of central tendency that provides an average representation of a set of data. Description The Measures of Central Tendency is an important concept in statistics, used to summarize data effectively. In real-world applications, the Measures of Central Tendency helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5.	Data Analysis
Definition--Measures of Central Tendency--Average	Average Topic Statistics Definition The average is a measure of central tendency, calculated by dividing the sum of values by their count. Description In statistics, the average is crucial for analyzing data sets, revealing trends, and providing insight into overall performance. It’s applicable in various fields, from school grades to business metrics. For example, if a student scores 80, 90, and 100 on three exams, the average can be calculated as follows: Average = (80 + 90 + 100) / 3 = 90. The average is essential in math education as it forms a foundational concept for more advanced statistical analyses.	Data Analysis
Definition--Measures of Central Tendency--Average Speed	Average Speed Topic Statistics Definition Average speed is the total distance traveled divided by the total time taken. Description This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.	Data Analysis
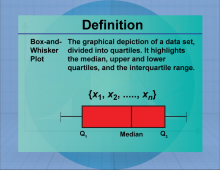
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Histogram	Histogram Topic Statistics Definition A histogram is a graphical representation of data distribution using bars of different heights. Description Histograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference.	Data Analysis
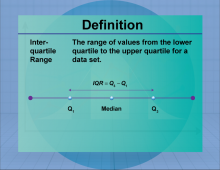
Definition--Measures of Central Tendency--Interquartile Range	Interquartile Range Topic Statistics Definition The interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. Description The IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability.	Data Analysis
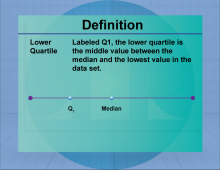
Definition--Measures of Central Tendency--Lower Quartile	Lower Quartile Topic Statistics Definition The lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. Description The lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Mean	Mean Topic Statistics Definition The mean is a measure of central tendency that provides an average representation of a set of data. Description The Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5.	Data Analysis
Definition--Measures of Central Tendency--Median	Median Topic Statistics Definition The median is a measure of central tendency that provides the middle value of a data set.. Description The Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean.	Data Analysis
Definition--Measures of Central Tendency--Median of an Even Data Set	Median of an Even Data Set Topic Statistics Definition The median of an even data set is the mean of two of the terms. Description The Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms.	Data Analysis
Definition--Measures of Central Tendency--Median of an Odd Data Set	Median of an Odd Data Set Topic Statistics Definition The median of an odd data set is one of the terms in the data set. Description The Median is the middle term of a data set. If the data set consists of an odd number of terms, no matter how many terms there are, the Median will be the middle term of that set. In mathematics education, understanding median of an odd data set is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Mode	Mode Topic Statistics Definition The mode is the most frequent data item.. Description The Mode is an important concept in statistics, used to summarize data effectively. It is the most frequent data item in a data set. A data set can have more than one mode. In mathematics education, understanding mode is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Mode of Categorical Data	Mode of Categorical Data Topic Statistics Definition The mode of categorical data is the most frequent item in a categorical data set. Description The Mode of Categorical Data is useful for finding the most frequent data item used with non-numerical data. For example, preferences for discrete characteristics can result in a mode.	Data Analysis
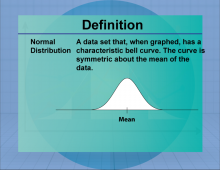
Definition--Measures of Central Tendency--Normal Distribution	Normal Distribution Topic Statistics Definition The normal distribution is a measure of central tendency that provides an average representation of a set of data. Description The Normal Distribution is an important concept in statistics, used to summarize data effectively. In real-world applications, the Normal Distribution helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research.	Data Analysis
Definition--Measures of Central Tendency--Outlier	Outlier Topic Statistics Definition The outlier is is an extreme value for a data set. Description The Outlier is an important concept in statistics. While it doesn't represent the average data set, it does set the range of extreme values in the data set. An outlier can be extremely large or small. In mathematics education, understanding outlier is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
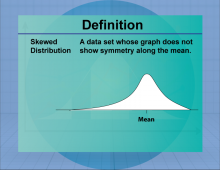
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis