
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 17: Scaling One Dimension
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Animated Math Clip Art--3D Geometry--Surface Area | Surface AreaTopic3D Geometry DescriptionThis animation illustrates the concept of surface area for a 3D shape. It shows how the surface of a three-dimensional object can be "unfolded" or "unwrapped" to reveal all its faces or surfaces, which can then be measured to calculate the total surface area. Using animated math clip art like this helps students visualize the abstract concept of surface area. Teachers can use this to explain how to calculate surface area for various 3D shapes and discuss real-world applications of this concept. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Tetrahedron | TetrahedronTopic3D Geometry DescriptionThis animation shows a tetrahedron, a three-dimensional shape with four triangular faces. It's the simplest of all the Platonic solids and has applications in both mathematics and chemistry. Animated math clip art like this is crucial for teaching as it allows students to visualize complex 3D shapes from different angles. Teachers can use this to discuss properties of polyhedra, symmetry, and geometric relationships. Here's a potential script for teachers: "Examine this tetrahedron. Count its faces, edges, and vertices. How does it compare to other 3D shapes we've studied? Can you think of any real-world objects that resemble a tetrahedron?" |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Tetrahedron with Horizontal Cross-Section | Tetrahedron with Horizontal Cross-SectionTopic3D Geometry DescriptionThis animation depicts a tetrahedron with a horizontal cross-section. It shows how slicing the tetrahedron parallel to its base results in a triangular cross-section that decreases in size as it moves towards the apex. Using animated math clip art like this helps students understand the internal structure of complex 3D shapes. Teachers can use this to discuss concepts such as similarity, proportions, and how cross-sections relate to the volume of a tetrahedron. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Tetrahedron with Vertical Cross-Section | Tetrahedron with Vertical Cross-SectionTopic3D Geometry DescriptionThis animation shows a tetrahedron with a vertical cross-section. It illustrates how slicing the tetrahedron vertically through its apex results in a triangular cross-section, revealing the internal structure and symmetry of the shape. Animated math clip art like this is valuable for teaching as it provides a different perspective on the internal geometry of complex 3D shapes. Teachers can use this to discuss concepts such as symmetry, slant height, and how vertical cross-sections relate to the surface area of a tetrahedron. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism | Triangular PrismTopic3D Geometry DescriptionThis animation depicts a triangular prism, a three-dimensional shape with two triangular bases and three rectangular faces. It's an important shape in geometry with various real-world applications. Using animated math clip art like this helps students visualize 3D shapes from different angles. Teachers can use this to explain concepts of volume, surface area, and properties of prisms. Here's a potential script for teachers: "Observe this triangular prism. Can you identify its bases and lateral faces? How would you calculate its volume and surface area? Can you think of any objects in real life that have this shape?" |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism with Horizontal Cross-Section | Triangular Prism with Horizontal Cross-SectionTopic3D Geometry DescriptionThis animation shows a triangular prism with a horizontal cross-section. It illustrates that slicing the prism parallel to its base results in a rectangular cross-section that varies in size depending on the location of the slice. Animated math clip art like this helps students understand the internal structure of prisms. Teachers can use this to discuss concepts such as congruence, cross-sectional area, and how this relates to the volume of a prism. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism with Vertical Cross-Section | Triangular Prism with Vertical Cross-SectionTopic3D Geometry DescriptionThis animation depicts a triangular prism with a vertical cross-section. It shows how slicing the prism vertically results in a triangular cross-section, and all such triangles are congruent along the length of the prism. Using animated math clip art like this provides students with a different perspective on the internal geometry of prisms. Teachers can use this to discuss concepts such as height, lateral area, and how vertical cross-sections relate to the surface area of a prism. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Vertical Cross-Section of a Rectangular Prism | Animated Math Clip Art: Vertical Cross-Section of a Rectangular Prism This animated math clip art visually demonstrates how a vertical plane intersects a rectangular prism, producing a two-dimensional cross-section. As the plane moves through the 3D shape, students can observe how the resulting cross-section remains a rectangle, reinforcing key geometric concepts related to slicing three-dimensional figures. Perfect for classroom instruction, this GIF animation helps students develop spatial reasoning by illustrating how a vertical slice interacts with the faces of a rectangular prism. This resource is particularly useful for teaching cross-sections in geometry and preparing students to understand more complex 3D slicing concepts. |
Rectangular Prisms |

|
Brief Review: Linear Equations in Standard Form | In this presentation we show how to convert a linear equation in Standard Form to a linear function in Slope Intercept Form. We go over the reason for such a conversion and applications that give rise to these equations. Note: The download is a PPT. |
Standard Form |

|
Closed Captioned Video: Algebra Applications: Linear Functions, Segment 2: Cycling | Closed Captioned Video: Algebra Applications: Linear Functions, Segment 2: CyclingTopicLinear Functions DescriptionApplies linear functions to cycling, calculating hill grades and distances using slope formulas and graphing. This video explores the mathematics behind Linear Functions, providing clear examples and engaging visuals to enhance understanding. It is an excellent resource for both introduction and reinforcement of key concepts. |
Special Functions and Applications of Linear Functions |

|
Closed Captioned Video: Algebra Applications: Linear Functions | Closed Captioned Video: Algebra Applications: Linear FunctionsTopicLinear Functions |
Special Functions and Applications of Linear Functions |

|
Closed Captioned Video: Algebra Applications: Linear Functions, 1 | Closed Captioned Video: Algebra Applications: Linear Functions, 1TopicLinear Functions DescriptionIntroduces linear functions with examples like staircases, explaining slope, intercepts, and applications in real-world scenarios. This video explores the mathematics behind Linear Functions, providing clear examples and engaging visuals to enhance understanding. It is an excellent resource for both introduction and reinforcement of key concepts. |
Special Functions and Applications of Linear Functions |

|
Closed Captioned Video: Algebra Applications: Linear Functions, 3 | Closed Captioned Video: Algebra Applications: Linear Functions, 3TopicLinear Functions DescriptionUses linear regression to analyze US oil consumption trends, projecting future usage and potential impact of Alaskan oil production. This video explores the mathematics behind Linear Functions, providing clear examples and engaging visuals to enhance understanding. It is an excellent resource for both introduction and reinforcement of key concepts. |
Special Functions and Applications of Linear Functions |

|
Closed Captioned Video: Algebra Applications: Linear Functions, 4 | Closed Captioned Video: Algebra Applications: Linear Functions, 4TopicLinear Functions DescriptionModels maximum heart rate during aerobic exercise with linear equations, creating exercise charts for various age groups. This video explores the mathematics behind Linear Functions, providing clear examples and engaging visuals to enhance understanding. It is an excellent resource for both introduction and reinforcement of key concepts. |
Special Functions and Applications of Linear Functions |

|
Closed Captioned Video: Algebra Nspirations: Functions and Relations | Closed Captioned Video: Algebra Nspirations: Functions and Relations
Functions are relationships between quantities that change. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video explores the definition of a function, its vocabulary and notations, and distinguishes the concept of function from a general relation. Multiple representations of functions are provided using the TI-Nspire, while dynamic visuals and scenarios put them into real-world contexts. Concepts explored: functions, relations, equations, quadratic functions, linear functions, multiple representations. |
Applications of Functions and Relations, Conic Sections and Relations and Functions |

|
Closed Captioned Video: Algebra Nspirations: Linear Functions | Closed Captioned Video: Algebra Nspirations: Linear Functions
In this program, internationally acclaimed mathematics educator Dr. Monica Neagoy, explores the nature of linear functions through the use TI graphing calculators. Examples ranging from air travel, construction, engineering, and space travel provide real-world examples for discovering algebraic concepts. All examples are solved algebraically and then reinforced through the use of the TI-Nspire. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series. Concepts explored: Standard form, slope-intercept form, point-slope form, solving linear equations. |
Applications of Linear Functions |

|
Closed Captioned Video: Algebra Nspirations: Linear Functions, 1 | Closed Captioned Video: Algebra Nspirations: Linear Functions, Segment 1
In this Investigation we look at linear models for objects moving at a constant speed. This video is Segment 1 of a 4 segment series related to Algebra Nspirations: Linear Functions. Segments 1 and 2 are grouped together. |
Applications of Linear Functions |

|
Closed Captioned Video: Algebra Nspirations: Linear Functions, 3 | Closed Captioned Video: Algebra Nspirations: Linear Functions, Segment 3
In this Investigation we look at a linear regression for carbon dioxide emission data. This video is Segment 3 of a 4 segment series related to Algebra Nspirations: Linear Functions. Segments 3 and 4 are grouped together. |
Applications of Linear Functions |

|
Closed Captioned Video: Geometry Applications: 3D Geometry | Closed Captioned Video: Geometry Applications: 3D GeometryTopic3D Geometry |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 1 | Closed Captioned Video: Geometry Applications: 3D Geometry, 1Topic3D Geometry DescriptionDescription: This segment introduces Platonic solids, including tetrahedron, cube, and dodecahedron, emphasizing their congruent edges, vertices, and angles. It connects these geometric figures to both natural and man-made structures, setting the stage for exploring 3D geometry applications. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 2 | Closed Captioned Video: Geometry Applications: 3D Geometry, 2Topic3D Geometry DescriptionDescription: This segment explores pyramids, particularly Mayan and Egyptian structures, to distinguish rectangular and square bases. It discusses the volume of truncated pyramids using proportional relationships and introduces the concept of tiered volume reduction through geometric sequences. |
3-Dimensional Figures, Pyramids and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 3 | Closed Captioned Video: Geometry Applications: 3D Geometry, 3Topic3D Geometry DescriptionDescription: This segment examines cylinders, using the Shanghai Tower as a case study. It highlights how adjustments to height and radius affect volume and surface area, demonstrating these principles with geometric calculations and their architectural applications in energy efficiency. |
3-Dimensional Figures, Cylinders and Applications of 3D Geometry |
|
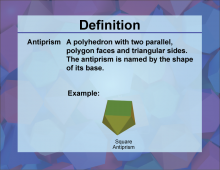
Definition--3D Geometry Concepts--Antiprism | AntiprismTopic3D Geometry DefinitionAn antiprism is a polyhedron composed of two parallel copies of an n-sided polygon, connected by an alternating band of triangles. DescriptionAntiprisms are fascinating three-dimensional geometric figures that play a significant role in the study of polyhedra and spatial geometry. Unlike prisms, which have rectangular lateral faces, antiprisms feature triangular faces connecting their two parallel polygonal bases. This unique structure gives antiprisms distinct properties and applications in various fields of mathematics and engineering. |
3-Dimensional Figures |
|
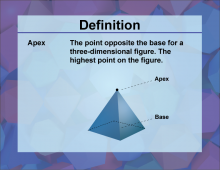
Definition--3D Geometry Concepts--Apex | ApexTopic3D Geometry DefinitionThe apex is the highest point or vertex of a three-dimensional figure, typically opposite to and furthest from its base. DescriptionIn the realm of three-dimensional geometry, the concept of an apex plays a crucial role in defining and understanding various geometric solids. The apex is particularly significant in figures such as cones and pyramids, where it represents the culminating point of the structure. For a cone, the apex is the single point at the top where all the lateral lines or edges converge. In a pyramid, it's the vertex where all the triangular faces meet, forming the pinnacle of the shape. |
3-Dimensional Figures |
|
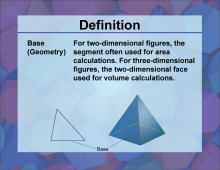
Definition--3D Geometry Concepts--Base (Geometry) | Geometric Base in 3D GeometryTopic3D Geometry DefinitionA geometric base is the face of a three-dimensional figure from which the height is measured. DescriptionIn the context of three-dimensional geometry, the term "geometric base" is crucial for understanding the structure and properties of various 3D shapes. The base of a 3D figure is typically a flat surface, often a polygon, from which the height of the figure is perpendicular. This concept is fundamental when calculating the volume and surface area of three-dimensional shapes such as prisms, cylinders, pyramids, and cones. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Cone | ConeTopic3D Geometry DefinitionA cone is a three-dimensional geometric shape that tapers smoothly from a flat, circular base to a point called the apex or vertex. DescriptionIn the realm of three-dimensional geometry, a cone is a significant shape due to its unique properties and applications. A cone is characterized by a circular base and a single apex. The line segments connecting the apex to the base form a curved surface, which is known as the lateral surface of the cone. The height of the cone is the perpendicular distance from the apex to the center of the base. |
Cones |
|
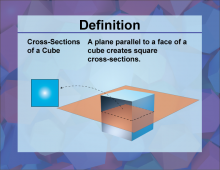
Definition--3D Geometry Concepts--Cross-sections of a Cube | Cross Sections of a CubeTopic3D Geometry DefinitionA cross-section of a cube is the intersection of a plane with the cube, resulting in a two-dimensional shape. DescriptionIn the study of three-dimensional geometry, understanding the cross-sections of a cube is vital for visualizing how 3D objects interact with planes. When a plane intersects a cube, the resulting shape can vary depending on the angle and position of the plane. Common cross-sections include squares, rectangles, and triangles. |
Cubes |
|
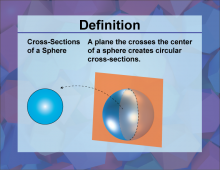
Definition--3D Geometry Concepts--Cross-Sections of a Sphere | Cross Sections of a SphereTopic3D Geometry DefinitionA cross-section of a sphere is the intersection of a plane with the sphere, resulting in a circle. DescriptionIn three-dimensional geometry, understanding the concept of cross-sections is crucial for visualizing and analyzing the properties of various 3D shapes. A sphere, which is a perfectly round geometrical object in three-dimensional space, can be intersected by a plane in various ways. When a plane cuts through a sphere, the shape of the intersection is always a circle. The size of this circle depends on the position of the plane relative to the center of the sphere. |
Spheres |
|
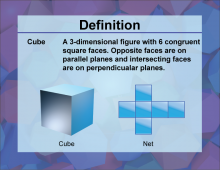
Definition--3D Geometry Concepts--Cube | CubeTopic3D Geometry DefinitionA cube is a three-dimensional geometric figure with six equal square faces, twelve equal edges, and eight vertices. DescriptionIn the realm of three-dimensional geometry, the cube stands out as one of the most fundamental and symmetrical shapes. Known for its six identical square faces, a cube is a regular polyhedron, meaning all its faces are congruent squares, and all its angles are right angles. This symmetry makes the cube a crucial shape in various fields, including mathematics, architecture, and computer graphics. |
Cubes |

|
Definition--3D Geometry Concepts--Cylinder | CylinderTopic3D Geometry DefinitionA cylinder is a three-dimensional geometric figure with two parallel circular bases connected by a curved surface at a fixed distance from each other. DescriptionIn the realm of three-dimensional geometry, a cylinder is a fundamental shape characterized by its two identical, parallel circular bases and a curved surface that connects these bases. The line segment joining the centers of the bases is called the axis of the cylinder, and it is perpendicular to the bases. The distance between the bases is the height of the cylinder, while the radius is the distance from the center to the edge of the base. |
Cylinders |

|
Definition--3D Geometry Concepts--Edge | EdgeTopic3D Geometry DefinitionAn edge in three-dimensional geometry is the line segment where two faces of a 3D shape meet. DescriptionIn the study of three-dimensional geometry, an edge is a fundamental concept that helps define the structure and properties of 3D shapes. Each edge is formed by the intersection of two faces, and it is a critical component in determining the overall shape and form of a 3D object. For instance, a cube has 12 edges, each formed by the meeting of two square faces. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Face | Face of a 3D FigureTopic3D Geometry DefinitionA face is a flat surface that forms part of the boundary of a three-dimensional figure. DescriptionIn the realm of three-dimensional geometry, the concept of a face is fundamental to understanding the structure and properties of 3D figures. A face represents one of the flat, two-dimensional surfaces that enclose a three-dimensional object. These surfaces play a crucial role in defining the shape, volume, and surface area of 3D figures. |
3-Dimensional Figures |
|
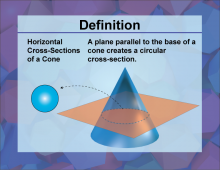
Definition--3D Geometry Concepts--Horizontal Cross-Sections of a Cone | Horizontal Cross-Sections of a ConeTopic3D Geometry DefinitionA horizontal cross-section of a cone is the circular shape obtained when a cone is intersected by a plane that is parallel to its base. |
Cones |
|
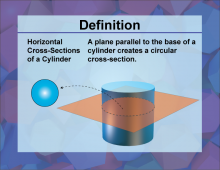
Definition--3D Geometry Concepts--Horizontal Cross-Sections of a Cylinder | Horizontal Cross Sections of a CylinderTopic3D Geometry DefinitionA horizontal cross-section of a cylinder is the intersection of the cylinder with a plane that is parallel to the base of the cylinder. DescriptionIn the context of three-dimensional geometry, understanding the concept of cross-sections is crucial. A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface. When a horizontal plane intersects a cylinder, the resulting cross-section is a circle. This concept is not only fundamental in geometry but also has practical applications in various fields. |
Cylinders |
|
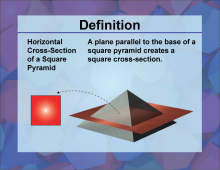
Definition--3D Geometry Concepts--Horizontal Cross-Sections of a Square Pyramid | Horizontal Cross Sections of a Square PyramidTopic3D Geometry. DefinitionA horizontal cross section of a square pyramid is a two-dimensional shape obtained by slicing the pyramid with a plane parallel to its base. |
Pyramids |
|
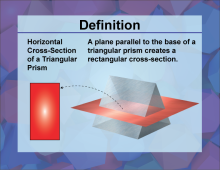
Definition--3D Geometry Concepts--Horizontal Cross-Sections of a Triangular Prism | Horizontal Cross Sections of a Triangular PrismTopic3D Geometry DefinitionA horizontal cross-section of a triangular prism is the shape obtained by cutting the prism with a plane parallel to its base. DescriptionIn three-dimensional geometry, a cross-section is the intersection of a plane with a solid figure. When this plane is parallel to the base of the solid, the resulting shape is called a horizontal cross-section. For a triangular prism with a rectangular base, this cross-section will always be a rectangle, similar in shape to the base of the prism. |
Triangular Prisms |
|
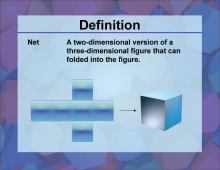
Definition--3D Geometry Concepts--Net | Net of a 3D FigureTopic3D Geometry DefinitionA net is a two-dimensional shape that can be folded to form a three-dimensional figure. DescriptionIn the realm of three-dimensional geometry, a net is an essential concept that helps in visualizing and constructing 3D shapes. A net is essentially a two-dimensional pattern that, when folded along specific lines, forms a three-dimensional object. This concept is particularly useful in understanding the properties and structures of 3D figures such as cubes, pyramids, and prisms. |
3-Dimensional Figures |
|
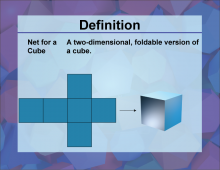
Definition--3D Geometry Concepts--Net for a Cube | Net for a CubeTopic3D Geometry DefinitionA net for a cube is a two-dimensional shape that can be folded to form a three-dimensional cube. DescriptionIn the realm of three-dimensional geometry, a net for a cube is a crucial concept. It represents a flattened out three-dimensional shape that can be folded along the edges to form a cube. This is an essential tool for visualizing and understanding how 3D shapes are constructed from 2D representations. |
Cubes |
|
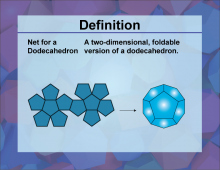
Definition--3D Geometry Concepts--Net for a Dodecahedron | Net for a DodecahedronTopic3D Geometry. DefinitionA net for a dodecahedron is a two-dimensional figure that can be folded to form a three-dimensional dodecahedron. DescriptionThe dodecahedron is one of the five Platonic solids, characterized by its twelve regular pentagonal faces, thirty edges, and twenty vertices. Understanding the net of a dodecahedron helps in visualizing and constructing this complex polyhedron from a flat sheet. |
3-Dimensional Figures |
|
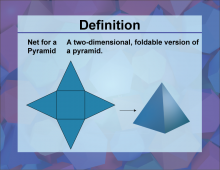
Definition--3D Geometry Concepts--Net for a Pyramid | Net for a PyramidTopic3D Geometry DefinitionA net for a pyramid is a two-dimensional representation that, when folded along its edges, forms the three-dimensional shape of a pyramid. DescriptionIn the study of three-dimensional geometry, understanding the concept of nets is crucial, particularly for complex shapes like pyramids. A net for a pyramid is essentially a flattened version of the 3D shape, showing all its faces in a single plane. This representation is invaluable for visualizing how the pyramid's surfaces connect and for calculating its surface area. |
Pyramids |
|
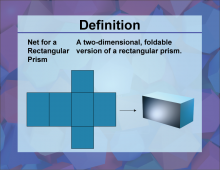
Definition--3D Geometry Concepts--Net for a Rectangular Prism | Net for a Rectangular PrismTopic3D Geometry DefinitionA net for a rectangular prism is a two-dimensional representation that, when folded, forms a three-dimensional rectangular prism. DescriptionIn the realm of three-dimensional geometry, the concept of a net is crucial for understanding how 3D shapes are constructed from 2D figures. A net for a rectangular prism is essentially a layout of all the faces of the prism in a single plane. This layout includes six rectangles that correspond to the six faces of the prism. By folding along the edges of these rectangles, one can recreate the three-dimensional shape of the rectangular prism. |
Rectangular Prisms |
|
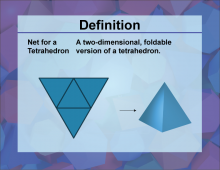
Definition--3D Geometry Concepts--Net for a Tetrahedron | Net for a TetrahedronTopic3D Geometry DefinitionA net for a tetrahedron is a two-dimensional pattern that can be folded to form a three-dimensional tetrahedron, which is a polyhedron with four triangular faces. DescriptionIn the realm of three-dimensional geometry, the concept of a net is crucial for understanding the structure and properties of polyhedra. A tetrahedron, one of the simplest forms of polyhedra, consists of four triangular faces, six edges, and four vertices. The net of a tetrahedron is a flat, two-dimensional figure that, when folded along its edges, forms the three-dimensional shape of the tetrahedron. |
3-Dimensional Figures |
|
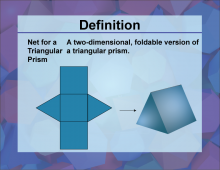
Definition--3D Geometry Concepts--Net for a Triangular Prism | Net for a Triangular PrismTopic3D Geometry DefinitionA net for a triangular prism is a two-dimensional figure that can be folded to form the surface of a three-dimensional triangular prism. DescriptionIn the context of three-dimensional geometry, a net is a crucial concept for understanding the surface area and structure of 3D shapes. Specifically, the net for a triangular prism consists of two triangular faces and three rectangular faces. When these faces are arranged in a specific two-dimensional pattern, they can be folded along the edges to form a triangular prism. |
Triangular Prisms |
|
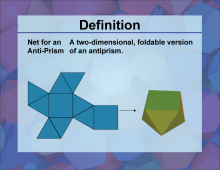
Definition--3D Geometry Concepts--Net for an Antiprism | Net for an AntiprismTopic3D Geometry. DefinitionA net for an antiprism is a two-dimensional shape that can be folded to form a three-dimensional antiprism, which is a type of polyhedron with two parallel polygonal bases connected by an alternating band of triangles. DescriptionIn the realm of three-dimensional geometry, an antiprism is a fascinating polyhedron that extends the concept of prisms. Unlike regular prisms, which have two parallel bases connected by rectangular faces, antiprisms have two parallel bases connected by an alternating band of triangles. This unique structure results in a more complex and often more visually interesting shape. |
3-Dimensional Figures |
|
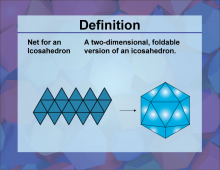
Definition--3D Geometry Concepts--Net for an Icosahedron | Net for an IcosahedronTopic3D Geometry DefinitionA net for an icosahedron is a two-dimensional flat pattern that, when folded along its edges, forms the surface of a three-dimensional icosahedron. DescriptionThe net for an icosahedron is a crucial concept in three-dimensional geometry, particularly in the study of polyhedra. An icosahedron is a regular polyhedron with 20 faces, each of which is an equilateral triangle. The net provides a visual representation of how these 20 triangular faces are connected and arranged in a flat pattern that can be folded to create the three-dimensional shape. |
3-Dimensional Figures |
|
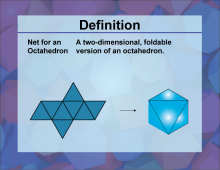
Definition--3D Geometry Concepts--Net for an Octahedron | Net for an OctahedronTopic3D Geometry DefinitionA net for an octahedron is a two-dimensional figure that can be folded to form a three-dimensional octahedron. DescriptionIn the realm of three-dimensional geometry, a net is a crucial concept that helps in visualizing and constructing 3D shapes from 2D representations. Specifically, a net for an octahedron consists of eight equilateral triangles arranged in a specific pattern. When these triangles are folded along the edges, they form an octahedron, which is a polyhedron with eight faces, twelve edges, and six vertices. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Platonic Solids | Platonic SolidsTopic3D Geometry DefinitionA Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space, where each face is a congruent regular polygon, and the same number of faces meet at each vertex. DescriptionPlatonic solids are fundamental constructs in the study of three-dimensional geometry. These solids are unique because they are the only five regular polyhedra that exist. Each Platonic solid has faces that are congruent regular polygons, and the same number of faces meet at each vertex, making them highly symmetrical and aesthetically pleasing. The five Platonic solids are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, each named for its number of faces. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Prism | PrismTopic3D Geometry DefinitionA prism is a three-dimensional solid object with two identical polygonal bases connected by parallelogram faces. DescriptionIn the realm of three-dimensional geometry, a prism is a polyhedron with two parallel, congruent bases connected by rectangular or parallelogram faces. The defining characteristic of a prism is that its cross-sections parallel to the bases are identical to the bases themselves. This property makes prisms a significant topic of study in geometry. |
3-Dimensional Figures |
|
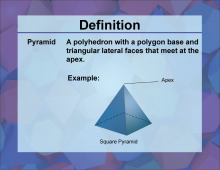
Definition--3D Geometry Concepts--Pyramid | PyramidTopic3D Geometry DefinitionA pyramid is a three-dimensional geometric figure with a polygonal base and triangular faces that converge to a single point called the apex. DescriptionIn the realm of three-dimensional geometry, a pyramid is a significant shape due to its unique properties and applications. A pyramid consists of a base that can be any polygon, such as a triangle, square, or pentagon, and triangular faces that connect each edge of the base to a single apex point. This structure results in a solid figure that is both aesthetically pleasing and structurally efficient. |
Pyramids |
|
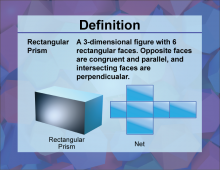
Definition--3D Geometry Concepts--Rectangular Prism | Rectangular PrismTopic3D Geometry DefinitionA rectangular prism is a three-dimensional figure with six rectangular faces, where opposite faces are congruent and parallel. DescriptionThe rectangular prism is a fundamental shape in three-dimensional geometry, serving as a building block for understanding more complex 3D structures. It is characterized by its three dimensions: length, width, and height, which are clearly labeled in the image. This shape is ubiquitous in both natural and man-made environments, making it a crucial concept for students to grasp. |
Rectangular Prisms |