
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 17: Scaling One Dimension
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
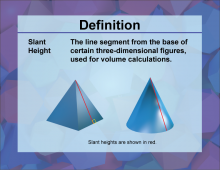
Definition--3D Geometry Concepts--Slant Height | Slant HeightTopic3D Geometry DefinitionSlant height is the distance measured along a lateral face from the base to the apex of a three-dimensional figure, such as a pyramid or a cone. DescriptionIn the context of three-dimensional geometry, the slant height is a crucial measurement for various solid figures, particularly right pyramids and right circular cones. It represents the shortest path along the surface of the figure from the apex (top point) to the base, distinguishing it from the vertical height which measures the perpendicular distance from the apex to the center of the base. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Sphere | SphereTopic3D Geometry DefinitionA sphere is a perfectly round three-dimensional geometric object in which every point on the surface is equidistant from the center. DescriptionIn the realm of three-dimensional geometry, a sphere is a fundamental shape characterized by its symmetry and uniformity. It is defined mathematically as the set of all points in space that are at a constant distance, known as the radius, from a fixed point called the center. This distance is the same in all directions, making the sphere a unique object with no edges or vertices. |
Spheres |
|
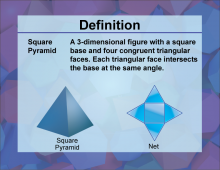
Definition--3D Geometry Concepts--Square Pyramid | Square PyramidTopic3D Geometry DefinitionA square pyramid is a three-dimensional geometric figure with a square base and four triangular faces that converge at a single point called the apex. |
Pyramids |

|
Definition--3D Geometry Concepts--Surface Area | Surface Area of 3D FiguresTopic3D Geometry DefinitionSurface area is the total area that the surface of a three-dimensional object occupies. DescriptionIn the realm of three-dimensional geometry, surface area is a fundamental concept that quantifies the extent of a 3D shape's exterior surface. This measure is crucial for various applications, including engineering, architecture, and everyday tasks. For example, when painting a room, the surface area of the walls, ceiling, and floor must be calculated to determine the amount of paint required. |
Surface Area |
|
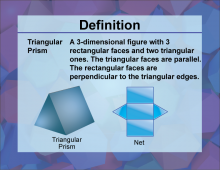
Definition--3D Geometry Concepts--Triangular Prism | Triangular PrismTopic3D Geometry DefinitionA triangular prism is a three-dimensional geometric solid with two congruent triangular bases and three rectangular faces. DescriptionThe triangular prism is a fundamental shape in three-dimensional geometry, playing a crucial role in understanding the properties of polyhedra and their applications in various fields. This prism is characterized by its unique structure, consisting of two parallel triangular bases connected by three rectangular faces. The shape of the triangular bases can vary, allowing for right, equilateral, isosceles, or scalene triangular prisms. |
Triangular Prisms |
|
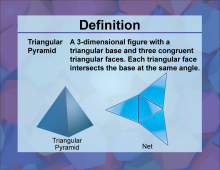
Definition--3D Geometry Concepts--Triangular Pyramid | Triangular PyramidTopic3D Geometry DefinitionA triangular pyramid, also known as a tetrahedron, is a three-dimensional geometric figure with four triangular faces, six edges, and four vertices. DescriptionIn the realm of three-dimensional geometry, the triangular pyramid holds significant relevance due to its unique properties and structural simplicity. Each triangular face of the pyramid converges at a single point known as the apex, forming a solid figure that is both symmetrical and aesthetically pleasing. This geometric shape is the simplest form of a pyramid and is often used in various fields such as architecture, molecular chemistry, and computer graphics. |
Pyramids |
|
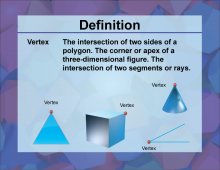
Definition--3D Geometry Concepts--Vertex | Vertex in 3D GeometryTopic3D Geometry DefinitionA vertex is a point where three or more edges meet in a three-dimensional figure. DescriptionIn the study of three-dimensional geometry, the term vertex is fundamental. A vertex is a critical point in any 3D geometric shape, marking the intersection of edges. For example, in a cube, each corner where the edges converge is a vertex. Vertices are essential in defining the shape and structure of 3D figures, as they help in understanding the spatial relationships between different parts of the figure. |
3-Dimensional Figures |
|
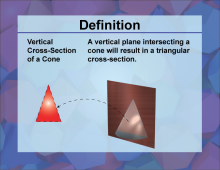
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Cone | Vertical Cross Sections of a ConeTopic3D Geometry DefinitionA vertical cross section of a cone is the intersection of the cone with a plane that passes through its vertex and base, resulting in a two-dimensional shape. |
Cones |
|
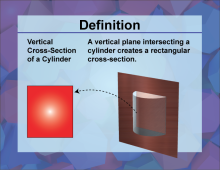
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Cylinder | Vertical Cross Sections of a CylinderTopic3D Geometry DefinitionA vertical cross-section of a cylinder is the intersection of the cylinder with a plane that is parallel to its axis. This cross-section is typically a rectangle if the plane cuts through the entire height of the cylinder. |
Cylinders |
|
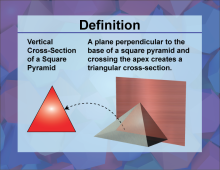
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Square Pyramid | Vertical Cross Sections of a Square PyramidTopic3D Geometry DefinitionA vertical cross section of a square pyramid is the intersection of the pyramid with a vertical plane that passes through its apex and base, resulting in a two-dimensional shape. |
Pyramids |
|
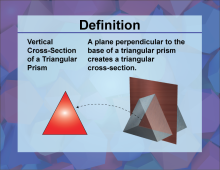
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Triangular Prism | Vertical Cross Sections of a Triangular PrismTopic3D Geometry DefinitionA vertical cross section of a triangular prism is a two-dimensional shape obtained by slicing the prism parallel to its height, revealing a triangular face. |
Triangular Prisms |

|
Definition--3D Geometry Concepts--Volume | VolumeTopic3D Geometry DefinitionVolume is the measure of the amount of space occupied by a three-dimensional object, expressed in cubic units. DescriptionVolume is a fundamental concept in the study of three-dimensional geometry. It quantifies the capacity of a 3D object, indicating how much space it occupies. This measurement is crucial in various fields, including mathematics, engineering, architecture, and physical sciences. |
Volume |
|
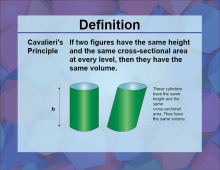
Definition--3D Geometry Concepts--Cavalieri's Principle | Cavalieri's PrincipleTopic3D Geometry DefinitionCavalieri's Principle states that if two solids are contained between two parallel planes, and every plane parallel to these planes intersects both solids in cross-sections of equal area, then the two solids have equal volumes. DescriptionCavalieri's Principle is a fundamental concept in three-dimensional geometry that provides a method for determining the volume of solids. Named after the Italian mathematician Bonaventura Cavalieri, this principle is particularly useful for comparing the volumes of solids that might not have straightforward geometric shapes. |
3-Dimensional Figures |

|
Definition--Functions and Relations Concepts--Absolute Value Function | Absolute Value Function
TopicFunctions and Relations DefinitionAn absolute value function is a function that contains an algebraic expression within absolute value symbols. It is defined as f(x)=|x| where |x| denotes the absolute value ofx. DescriptionThe absolute value function is significant in mathematics because it measures the distance of a number from zero on the number line, regardless of direction. This function is linear in nature, as it can be broken into two linear pieces: one for x≥0 and one for x<0 |
Special Functions |
|
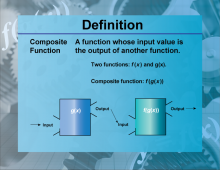
Definition--Functions and Relations Concepts--Composite Function | Composite FunctionTopicFunctions and Relations DefinitionA composite function is a function that is formed when one function is applied to the result of another function. DescriptionComposite functions are significant in mathematics because they allow the combination of two functions to form a new function. This is denoted as (f∘g)(x) = f(g(x)). Composite functions are widely used in various fields, including computer science for function composition in programming and in calculus for chain rule applications. For example, if f(x) = 2x and g(x) = x + 3, then the composite function (f∘g)(x) = f(g(x)) = 2(x + 3) = 2x+6 |
Composite Functions |
|
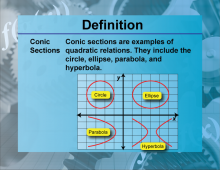
Definition--Functions and Relations Concepts--Conic Sections | Conic SectionsTopicFunctions and Relations DefinitionConic sections are the curves obtained by intersecting a plane with a double-napped cone. DescriptionConic sections include circles, ellipses, parabolas, and hyperbolas, which are fundamental in the study of geometry and algebra. These shapes are described by quadratic equations and have numerous applications in physics, engineering, and astronomy. For example, the orbits of planets are ellipses, and parabolic mirrors are used in telescopes and satellite dishes. The general quadratic equation for conic sections is Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 |
Conic Sections |
|
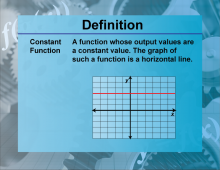
Definition--Functions and Relations Concepts--Constant Function | Constant FunctionTopicFunctions and Relations DefinitionA constant function is a function that always returns the same value, no matter the input. DescriptionThe constant function is one of the simplest types of functions in mathematics, expressed as f(x) = c |
Relations and Functions |
|
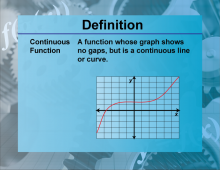
Definition--Functions and Relations Concepts--Continuous Function | Continuous FunctionTopicFunctions and Relations DefinitionA continuous function is a function that does not have any breaks, holes, or gaps in its domain. DescriptionContinuous functions are fundamental in calculus and mathematical analysis because they allow for the application of limits, derivatives, and integrals. A function f(x) is continuous if, for every point 𝑐 c in its domain, lim x→c f(x) = f(c) |
Relations and Functions |
|
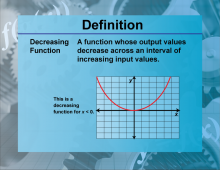
Definition--Functions and Relations Concepts--Decreasing Function | Decreasing FunctionTopicFunctions and Relations DefinitionA decreasing function is a function where the value of the function decreases as the input increases. DescriptionDecreasing functions are important in mathematics because they describe scenarios where an increase in one variable leads to a decrease in another. This is mathematically represented as f(x1) > f(x2) for any 𝑥1 < 𝑥2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Dependent Variable | Dependent VariableTopicFunctions and Relations DefinitionA dependent variable is a variable whose value depends on one or more other variables. |
Relations and Functions |
|
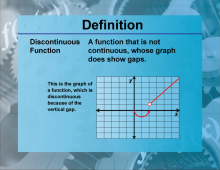
Definition--Functions and Relations Concepts--Discontinuous Function | Discontinuous FunctionTopicFunctions and Relations DefinitionA discontinuous function is a function that has one or more points where it is not continuous. |
Relations and Functions |
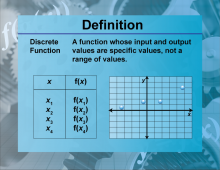
|
Definition--Functions and Relations Concepts--Discrete Functions | Discrete FunctionsTopicFunctions and Relations DefinitionDiscrete functions are functions that are defined only for a set of discrete points. |
Special Functions |

|
Definition--Functions and Relations Concepts--Distorting a Function Horizontally | Distorting a Function HorizontallyTopicFunctions and Relations DefinitionDistorting a function horizontally involves stretching or compressing the graph of the function along the x-axis. DescriptionHorizontal distortions of functions are significant because they alter the input values while maintaining the overall shape of the graph. This is mathematically represented as f(kx) where k is a constant. If k > 1, the function compresses horizontally, and if 0 < 𝑘 < 1, it stretches. |
Relations and Functions |
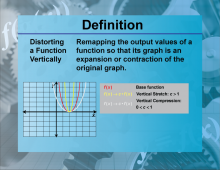
|
Definition--Functions and Relations Concepts--Distorting a Function Vertically | Distorting a Function VerticallyTopicFunctions and Relations DefinitionDistorting a function vertically involves stretching or compressing the graph of the function along the y-axis. DescriptionVertical distortions of functions are significant because they alter the output values while maintaining the overall shape of the graph. This is mathematically represented as kf(x) |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Domain of a Function | Domain of a FunctionTopicFunctions and Relations DefinitionThe domain of a function is the set of all possible input values (x-values) for which the function is defined. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Even Function | Even FunctionTopicFunctions and Relations DefinitionAn even function is a function that satisfies the condition f(x) = f(−x) for all x in its domain. DescriptionEven functions are important in mathematics because they exhibit symmetry about the y-axis. This property is useful in various fields, including physics and engineering, where symmetry simplifies analysis and problem-solving. For example, the function f(x)=x2 |
Relations and Functions |
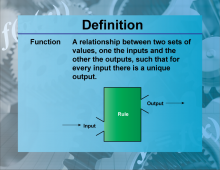
|
Definition--Functions and Relations Concepts--Function | FunctionTopicFunctions and Relations DefinitionA function is a relation that uniquely associates each element of a set with exactly one element of another set. |
Relations and Functions |
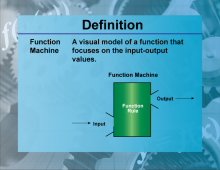
|
Definition--Functions and Relations Concepts--Function Machine | Function MachineTopicFunctions and Relations DefinitionA function machine is a conceptual tool used to understand how functions work by visualizing inputs and outputs. DescriptionThe function machine is a useful educational tool that helps students grasp the concept of functions by visualizing the process of converting inputs into outputs. It emphasizes the idea that a function takes an input, processes it according to a specific rule, and produces an output. For example, if the function is f(x) = x + 2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Function Notation | Function NotationTopicFunctions and Relations DefinitionFunction notation is a way to represent functions in the form f(x), where f denotes the function and x denotes the input variable. DescriptionFunction notation is a standardized way to write functions, making it easier to understand and communicate mathematical relationships. It is widely used in algebra, calculus, and other branches of mathematics. For example, the notation f(x) = x2 |
Relations and Functions |
|
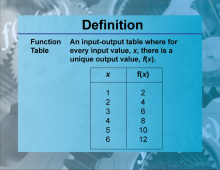
Definition--Functions and Relations Concepts--Function Table | Function TableTopicFunctions and Relations DefinitionA function table is a table that lists input values and their corresponding output values for a given function. DescriptionFunction tables are useful tools in mathematics for organizing and analyzing the relationship between inputs and outputs of a function. They help in visualizing how a function behaves and in identifying patterns. For example, a function table for f(x) = 2x + 1 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Graphs of Functions | Graphs of FunctionsTopicFunctions and Relations DefinitionGraphs of functions are visual representations of the relationship between input values and output values of a function. DescriptionGraphs of functions are essential tools in mathematics for visualizing how a function behaves. They provide a clear picture of the relationship between the input and output values, making it easier to analyze and interpret the function. For example, the graph of f(x) = x2 |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Graphs of Relations | Graphs of RelationsTopicFunctions and Relations DefinitionGraphs of relations are visual representations of the relationship between two sets of values, not necessarily functions. |
Relations and Functions |
|
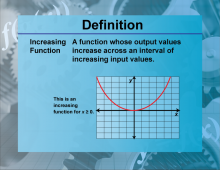
Definition--Functions and Relations Concepts--Increasing Function | Increasing FunctionTopicFunctions and Relations DefinitionAn increasing function is a function where the value of the function increases as the input increases. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Independent Variable | Independent VariableTopicFunctions and Relations DefinitionAn independent variable is a variable that represents the input or cause and is manipulated to observe its effect on the dependent variable. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Inverse Function | Inverse FunctionTopicFunctions and Relations DefinitionAn inverse function is a function that reverses the effect of the original function, such that f(f−1(x)) = x. |
Functions and Their Inverses |
|
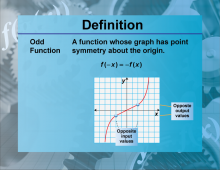
Definition--Functions and Relations Concepts--Odd Function | Odd FunctionTopicFunctions and Relations DefinitionAn odd function is a function that satisfies the condition f(−x) = −f(x) for all x in its domain. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Parametric Equations | Parametric EquationsTopicFunctions and Relations DefinitionParametric equations are a set of equations that express the coordinates of the points of a curve as functions of a variable called a parameter. |
Relations and Functions |

|
Definition--Functions and Relations Concepts--Piecewise Functions | Piecewise FunctionsTopicFunctions and Relations DefinitionPiecewise functions are functions defined by multiple sub-functions, each applying to a certain interval of the domain. |
Special Functions |

|
Definition--Functions and Relations Concepts--Range of a Function | Range of a FunctionTopicFunctions and Relations DefinitionThe range of a function is the set of all possible output values (y-values) that the function can produce. DescriptionUnderstanding the range of a function is crucial in mathematics because it defines the scope of possible outputs. The range is determined by the function's rule and the domain. For example, the range of the function f(x) = x2 |
Relations and Functions |
|
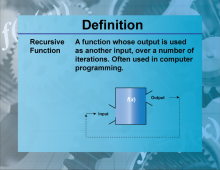
Definition--Functions and Relations Concepts--Recursive Function | Recursive FunctionTopicFunctions and Relations DefinitionA recursive function is a function that calls itself in its definition. DescriptionRecursive functions are important in mathematics and computer science because they provide a way to solve problems by breaking them down into simpler sub-problems. They are defined by a base case and a recursive case. For example, the factorial function f(n) = n⋅f(n−1) with f(0)=1 |
Relations and Functions |
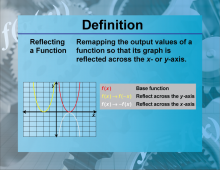
|
Definition--Functions and Relations Concepts--Reflecting a Function | Reflecting a FunctionTopicFunctions and Relations DefinitionReflecting a function involves flipping the graph of the function over a specified axis. DescriptionReflecting functions is significant in mathematics because it helps in understanding the symmetry and transformations of functions. A function can be reflected over the x-axis or y-axis, changing its orientation. For example, reflecting the function f(x) = x2 |
Relations and Functions |
|
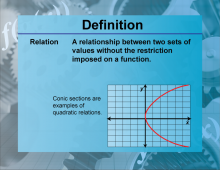
Definition--Functions and Relations Concepts--Relation | RelationTopicFunctions and Relations DefinitionA relation is a set of ordered pairs, where each element from one set is paired with an element from another set. |
Relations and Functions |
|
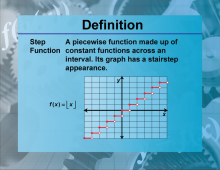
Definition--Functions and Relations Concepts--Step Function | Step FunctionTopicFunctions and Relations DefinitionA step function is a function that increases or decreases abruptly at certain points, creating a series of steps. |
Special Functions |
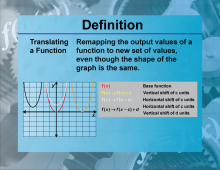
|
Definition--Functions and Relations Concepts--Translating a Function | Translating a FunctionTopicFunctions and Relations DefinitionTranslating a function involves shifting the graph of the function horizontally, vertically, or both, without changing its shape. DescriptionTranslating functions is significant in mathematics because it helps in understanding how functions behave under shifts. A function can be translated horizontally by adding or subtracting a constant to the input, and vertically by adding or subtracting a constant to the output. For example, translating the function f(x) = x2 horizontally by 2 units results in |
Relations and Functions |
|
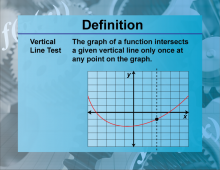
Definition--Functions and Relations Concepts--Vertical Line Test | Vertical Line TestTopicFunctions and Relations DefinitionThe vertical line test is a method used to determine if a graph represents a function by checking if any vertical line intersects the graph more than once. DescriptionThe vertical line test is important in mathematics because it helps in identifying whether a given graph represents a function. If a vertical line intersects the graph at more than one point, then the graph does not represent a function. This test is used in various fields, including computer science for validating functions in programming and in mathematics for analyzing graphs. For example, the graph of |
Relations and Functions |
|
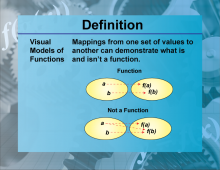
Definition--Functions and Relations Concepts--Visual Models of Functions | Visual Models of FunctionsTopicFunctions and Relations DefinitionVisual models of functions are graphical representations that illustrate the relationship between input and output values of functions. DescriptionVisual models of functions are important in mathematics because they provide a clear and intuitive way to understand how functions behave. These models include graphs, tables, and diagrams that show the relationship between input and output values. For example, the graph of f(x) = x2 |
Relations and Functions |
|
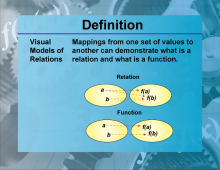
Definition--Functions and Relations Concepts--Visual Models of Relations | Visual Models of RelationsTopicFunctions and Relations DefinitionVisual models of relations are graphical representations that illustrate the relationship between two sets of values, not necessarily functions. |
Relations and Functions |
|
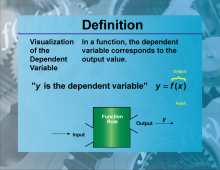
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable | Visualization of the Dependent VariableTopicFunctions and Relations DefinitionVisualization of the dependent variable involves graphically representing the outcomes or responses that depend on the independent variable. |
Relations and Functions |
|
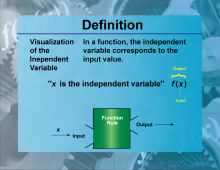
Definition--Functions and Relations Concepts--Visualization of the Independent Variable | Visualization of the Independent VariableTopicFunctions and Relations DefinitionVisualization of the independent variable involves graphically representing the variable that is manipulated to observe its effect on the dependent variable. |
Relations and Functions |

|
Geometry Applications Teachers Guide: 3D Geometry | Geometry Applications Teachers Guide: 3D Geometry
This is the Teacher's Guide that accompanies Geometry Applications: 3D Geometry. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of 3D Geometry |