Illustrative Math Alignment: Grade 8 Unit 3

Functions and Volume

Lesson 18: Scaling Two Dimensions

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
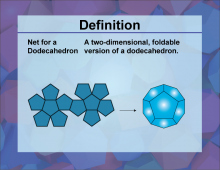
Definition--3D Geometry Concepts--Net for a Dodecahedron	Net for a Dodecahedron Topic 3D Geometry. Definition A net for a dodecahedron is a two-dimensional figure that can be folded to form a three-dimensional dodecahedron. Description The dodecahedron is one of the five Platonic solids, characterized by its twelve regular pentagonal faces, thirty edges, and twenty vertices. Understanding the net of a dodecahedron helps in visualizing and constructing this complex polyhedron from a flat sheet.	3-Dimensional Figures
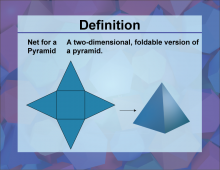
Definition--3D Geometry Concepts--Net for a Pyramid	Net for a Pyramid Topic 3D Geometry Definition A net for a pyramid is a two-dimensional representation that, when folded along its edges, forms the three-dimensional shape of a pyramid. Description In the study of three-dimensional geometry, understanding the concept of nets is crucial, particularly for complex shapes like pyramids. A net for a pyramid is essentially a flattened version of the 3D shape, showing all its faces in a single plane. This representation is invaluable for visualizing how the pyramid's surfaces connect and for calculating its surface area.	Pyramids
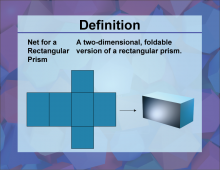
Definition--3D Geometry Concepts--Net for a Rectangular Prism	Net for a Rectangular Prism Topic 3D Geometry Definition A net for a rectangular prism is a two-dimensional representation that, when folded, forms a three-dimensional rectangular prism. Description In the realm of three-dimensional geometry, the concept of a net is crucial for understanding how 3D shapes are constructed from 2D figures. A net for a rectangular prism is essentially a layout of all the faces of the prism in a single plane. This layout includes six rectangles that correspond to the six faces of the prism. By folding along the edges of these rectangles, one can recreate the three-dimensional shape of the rectangular prism.	Rectangular Prisms
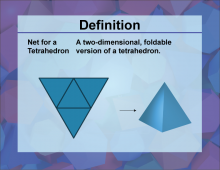
Definition--3D Geometry Concepts--Net for a Tetrahedron	Net for a Tetrahedron Topic 3D Geometry Definition A net for a tetrahedron is a two-dimensional pattern that can be folded to form a three-dimensional tetrahedron, which is a polyhedron with four triangular faces. Description In the realm of three-dimensional geometry, the concept of a net is crucial for understanding the structure and properties of polyhedra. A tetrahedron, one of the simplest forms of polyhedra, consists of four triangular faces, six edges, and four vertices. The net of a tetrahedron is a flat, two-dimensional figure that, when folded along its edges, forms the three-dimensional shape of the tetrahedron.	3-Dimensional Figures
Definition--3D Geometry Concepts--Net for a Triangular Prism	Net for a Triangular Prism Topic 3D Geometry Definition A net for a triangular prism is a two-dimensional figure that can be folded to form the surface of a three-dimensional triangular prism. Description In the context of three-dimensional geometry, a net is a crucial concept for understanding the surface area and structure of 3D shapes. Specifically, the net for a triangular prism consists of two triangular faces and three rectangular faces. When these faces are arranged in a specific two-dimensional pattern, they can be folded along the edges to form a triangular prism.	Triangular Prisms
Definition--3D Geometry Concepts--Net for an Antiprism	Net for an Antiprism Topic 3D Geometry. Definition A net for an antiprism is a two-dimensional shape that can be folded to form a three-dimensional antiprism, which is a type of polyhedron with two parallel polygonal bases connected by an alternating band of triangles. Description In the realm of three-dimensional geometry, an antiprism is a fascinating polyhedron that extends the concept of prisms. Unlike regular prisms, which have two parallel bases connected by rectangular faces, antiprisms have two parallel bases connected by an alternating band of triangles. This unique structure results in a more complex and often more visually interesting shape.	3-Dimensional Figures
Definition--3D Geometry Concepts--Net for an Icosahedron	Net for an Icosahedron Topic 3D Geometry Definition A net for an icosahedron is a two-dimensional flat pattern that, when folded along its edges, forms the surface of a three-dimensional icosahedron. Description The net for an icosahedron is a crucial concept in three-dimensional geometry, particularly in the study of polyhedra. An icosahedron is a regular polyhedron with 20 faces, each of which is an equilateral triangle. The net provides a visual representation of how these 20 triangular faces are connected and arranged in a flat pattern that can be folded to create the three-dimensional shape.	3-Dimensional Figures
Definition--3D Geometry Concepts--Net for an Octahedron	Net for an Octahedron Topic 3D Geometry Definition A net for an octahedron is a two-dimensional figure that can be folded to form a three-dimensional octahedron. Description In the realm of three-dimensional geometry, a net is a crucial concept that helps in visualizing and constructing 3D shapes from 2D representations. Specifically, a net for an octahedron consists of eight equilateral triangles arranged in a specific pattern. When these triangles are folded along the edges, they form an octahedron, which is a polyhedron with eight faces, twelve edges, and six vertices.	3-Dimensional Figures
Definition--3D Geometry Concepts--Platonic Solids	Platonic Solids Topic 3D Geometry Definition A Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space, where each face is a congruent regular polygon, and the same number of faces meet at each vertex. Description Platonic solids are fundamental constructs in the study of three-dimensional geometry. These solids are unique because they are the only five regular polyhedra that exist. Each Platonic solid has faces that are congruent regular polygons, and the same number of faces meet at each vertex, making them highly symmetrical and aesthetically pleasing. The five Platonic solids are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, each named for its number of faces.	3-Dimensional Figures
Definition--3D Geometry Concepts--Prism	Prism Topic 3D Geometry Definition A prism is a three-dimensional solid object with two identical polygonal bases connected by parallelogram faces. Description In the realm of three-dimensional geometry, a prism is a polyhedron with two parallel, congruent bases connected by rectangular or parallelogram faces. The defining characteristic of a prism is that its cross-sections parallel to the bases are identical to the bases themselves. This property makes prisms a significant topic of study in geometry.	3-Dimensional Figures
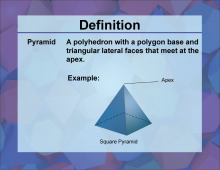
Definition--3D Geometry Concepts--Pyramid	Pyramid Topic 3D Geometry Definition A pyramid is a three-dimensional geometric figure with a polygonal base and triangular faces that converge to a single point called the apex. Description In the realm of three-dimensional geometry, a pyramid is a significant shape due to its unique properties and applications. A pyramid consists of a base that can be any polygon, such as a triangle, square, or pentagon, and triangular faces that connect each edge of the base to a single apex point. This structure results in a solid figure that is both aesthetically pleasing and structurally efficient.	Pyramids
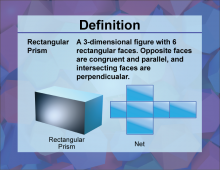
Definition--3D Geometry Concepts--Rectangular Prism	Rectangular Prism Topic 3D Geometry Definition A rectangular prism is a three-dimensional figure with six rectangular faces, where opposite faces are congruent and parallel. Description The rectangular prism is a fundamental shape in three-dimensional geometry, serving as a building block for understanding more complex 3D structures. It is characterized by its three dimensions: length, width, and height, which are clearly labeled in the image. This shape is ubiquitous in both natural and man-made environments, making it a crucial concept for students to grasp.	Rectangular Prisms
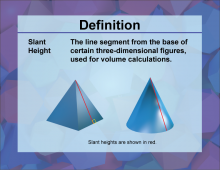
Definition--3D Geometry Concepts--Slant Height	Slant Height Topic 3D Geometry Definition Slant height is the distance measured along a lateral face from the base to the apex of a three-dimensional figure, such as a pyramid or a cone. Description In the context of three-dimensional geometry, the slant height is a crucial measurement for various solid figures, particularly right pyramids and right circular cones. It represents the shortest path along the surface of the figure from the apex (top point) to the base, distinguishing it from the vertical height which measures the perpendicular distance from the apex to the center of the base.	3-Dimensional Figures
Definition--3D Geometry Concepts--Sphere	Sphere Topic 3D Geometry Definition A sphere is a perfectly round three-dimensional geometric object in which every point on the surface is equidistant from the center. Description In the realm of three-dimensional geometry, a sphere is a fundamental shape characterized by its symmetry and uniformity. It is defined mathematically as the set of all points in space that are at a constant distance, known as the radius, from a fixed point called the center. This distance is the same in all directions, making the sphere a unique object with no edges or vertices.	Spheres
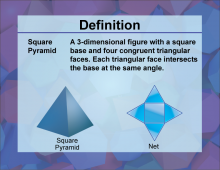
Definition--3D Geometry Concepts--Square Pyramid	Square Pyramid Topic 3D Geometry Definition A square pyramid is a three-dimensional geometric figure with a square base and four triangular faces that converge at a single point called the apex.	Pyramids
Definition--3D Geometry Concepts--Surface Area	Surface Area of 3D Figures Topic 3D Geometry Definition Surface area is the total area that the surface of a three-dimensional object occupies. Description In the realm of three-dimensional geometry, surface area is a fundamental concept that quantifies the extent of a 3D shape's exterior surface. This measure is crucial for various applications, including engineering, architecture, and everyday tasks. For example, when painting a room, the surface area of the walls, ceiling, and floor must be calculated to determine the amount of paint required.	Surface Area
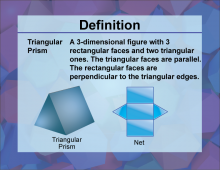
Definition--3D Geometry Concepts--Triangular Prism	Triangular Prism Topic 3D Geometry Definition A triangular prism is a three-dimensional geometric solid with two congruent triangular bases and three rectangular faces. Description The triangular prism is a fundamental shape in three-dimensional geometry, playing a crucial role in understanding the properties of polyhedra and their applications in various fields. This prism is characterized by its unique structure, consisting of two parallel triangular bases connected by three rectangular faces. The shape of the triangular bases can vary, allowing for right, equilateral, isosceles, or scalene triangular prisms.	Triangular Prisms
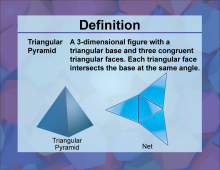
Definition--3D Geometry Concepts--Triangular Pyramid	Triangular Pyramid Topic 3D Geometry Definition A triangular pyramid, also known as a tetrahedron, is a three-dimensional geometric figure with four triangular faces, six edges, and four vertices. Description In the realm of three-dimensional geometry, the triangular pyramid holds significant relevance due to its unique properties and structural simplicity. Each triangular face of the pyramid converges at a single point known as the apex, forming a solid figure that is both symmetrical and aesthetically pleasing. This geometric shape is the simplest form of a pyramid and is often used in various fields such as architecture, molecular chemistry, and computer graphics.	Pyramids
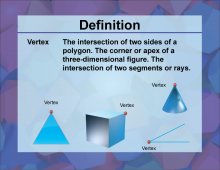
Definition--3D Geometry Concepts--Vertex	Vertex in 3D Geometry Topic 3D Geometry Definition A vertex is a point where three or more edges meet in a three-dimensional figure. Description In the study of three-dimensional geometry, the term vertex is fundamental. A vertex is a critical point in any 3D geometric shape, marking the intersection of edges. For example, in a cube, each corner where the edges converge is a vertex. Vertices are essential in defining the shape and structure of 3D figures, as they help in understanding the spatial relationships between different parts of the figure.	3-Dimensional Figures
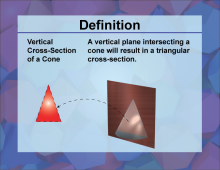
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Cone	Vertical Cross Sections of a Cone Topic 3D Geometry Definition A vertical cross section of a cone is the intersection of the cone with a plane that passes through its vertex and base, resulting in a two-dimensional shape.	Cones
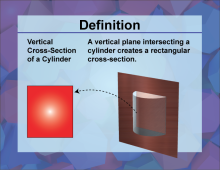
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Cylinder	Vertical Cross Sections of a Cylinder Topic 3D Geometry Definition A vertical cross-section of a cylinder is the intersection of the cylinder with a plane that is parallel to its axis. This cross-section is typically a rectangle if the plane cuts through the entire height of the cylinder.	Cylinders
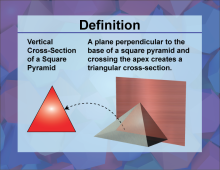
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Square Pyramid	Vertical Cross Sections of a Square Pyramid Topic 3D Geometry Definition A vertical cross section of a square pyramid is the intersection of the pyramid with a vertical plane that passes through its apex and base, resulting in a two-dimensional shape.	Pyramids
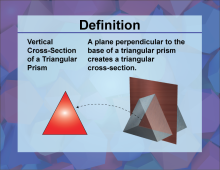
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Triangular Prism	Vertical Cross Sections of a Triangular Prism Topic 3D Geometry Definition A vertical cross section of a triangular prism is a two-dimensional shape obtained by slicing the prism parallel to its height, revealing a triangular face.	Triangular Prisms
Definition--3D Geometry Concepts--Volume	Volume Topic 3D Geometry Definition Volume is the measure of the amount of space occupied by a three-dimensional object, expressed in cubic units. Description Volume is a fundamental concept in the study of three-dimensional geometry. It quantifies the capacity of a 3D object, indicating how much space it occupies. This measurement is crucial in various fields, including mathematics, engineering, architecture, and physical sciences.	Volume
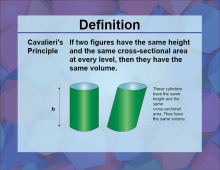
Definition--3D Geometry Concepts--Cavalieri's Principle	Cavalieri's Principle Topic 3D Geometry Definition Cavalieri's Principle states that if two solids are contained between two parallel planes, and every plane parallel to these planes intersects both solids in cross-sections of equal area, then the two solids have equal volumes. Description Cavalieri's Principle is a fundamental concept in three-dimensional geometry that provides a method for determining the volume of solids. Named after the Italian mathematician Bonaventura Cavalieri, this principle is particularly useful for comparing the volumes of solids that might not have straightforward geometric shapes.	3-Dimensional Figures
Desmos Activity: Exploring Celsius-Fahrenheit Temperature Conversions	Explore Fahrenheit-vs-Celsius graphs using this Desmos graphing calculator activity. In this activity explore linear functions of the form y = mx + b. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Graphs of Linear Functions
Desmos Activity: Exploring Cost-Versus-Time Graphs	Explore Cost-vs-Time graphs using this Desmos graphing calculator activity. In this activity explore linear functions of the form y = mx. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Graphs of Linear Functions
Desmos Activity: Exploring Cost-Versus-Time Graphs 2	Explore Cost-vs-Time graphs using this Desmos graphing calculator activity. In this activity explore linear functions of the form y = mx + b. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Graphs of Linear Functions
Desmos Activity: Exploring Cricket Chirps Vs. Temperature	Explore Cricket Chirps-vs-Temperature graphs using this Desmos graphing calculator activity. In this activity explore linear functions of the form y = mx + b. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Applications of Linear Functions
Desmos Activity: Exploring Distance-Versus-Time Graphs	Explore Distance-vs-Time graphs using this Desmos graphing calculator activity. This activity explores linear functions of the form y = mx. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Graphs of Linear Functions
Desmos Activity: Exploring Distance-Versus-Time Graphs 2	Explore Distance-vs-Time graphs using this Desmos graphing calculator activity. This activity explores linear functions of the form y = mx + b. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Graphs of Linear Functions
Desmos Activity: Exploring Hooke's Law	Explore Hooke's Law using this Desmos graphing calculator activity. In this activity explore linear functions of the form y = mx. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Graphs of Linear Functions and Proportions
Desmos Activity: Linear Functions 3: y = mx + b	In this graphing calculator activity, have your students explore linear functions of the form y = mx + b. This Desmos template allows students to explore the effect of changes in the slope (m) and the y-intercept (b) have on the graph of the line. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear functions. Note: The download is a PDF worksheet. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Slope-Intercept Form
Geometry Applications Teachers Guide: 3D Geometry	Geometry Applications Teachers Guide: 3D Geometry This is the Teacher's Guide that accompanies Geometry Applications: 3D Geometry. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of 3D Geometry
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2	Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2 Topic Geometric Models	Surface Area, Volume and Rational Functions and Equations
Google Earth Voyager Story: The Mathematics of Pyramids, Part 1	Google Earth Voyager Story: The Mathematics of Pyramids, Part 1 Topic Geometric Models	Pyramids
Google Earth Voyager Story: The Mathematics of Pyramids, Part 2	Google Earth Voyager Story: The Mathematics of Pyramids, Part 2 Topic Geometric Models	Pyramids
INSTRUCTIONAL RESOURCE: Algebra Application: Creating an Exercise Chart	INSTRUCTIONAL RESOURCE: Algebra Application: Creating an Exercise Chart In this Algebra Application, students develop a linear mathematical model based on the maximum heart rate during exercise based on age. Using this model, students investigate heart rate for moderate and vigorous workouts. The math topics covered include: Mathematical modeling, Linear functions, Families of functions, Computational thinking. The culminating activity is for students to create a simple program (using either a spreadsheet or a programming language like Python) to develop an exercise chart. This is a great back-to-school activity for middle school or high school students. A relevant real-world application allows them to review math concepts.	Applications of Linear Functions and Slope-Intercept Form
INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter	INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter In this Algebra Application, students study the direction between diameter and circumference of a circle. Through measurement and data gathering students analyze the line of best fit and explore ways of calculating pi. The math topics covered include: Mathematical modeling, Linear functions, Data gathering and analysis, Ratios, Direct variation. This is a great back-to-school activity for middle school or high school students. This is also a great crossover activity that ties algebra and geometry.	Applications of Linear Functions, Applications of Ratios, Proportions, and Percents and Applications of Circles
Instructional Resource: Applications of Linear Functions: Circumference vs. Diameter	In this Slide Show, apply concepts of linear functions to the context of circumference vs. diameter. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
Instructional Resource: Applications of Linear Functions: Cost vs. Time	In this Slide Show, apply concepts of linear functions to the context of cost vs. time data and graphs. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
Instructional Resource: Applications of Linear Functions: Cricket Chirps	In this Slide Show, apply concepts of linear functions to the context of cricket chirps. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
Instructional Resource: Applications of Linear Functions: Distance vs. Time	In this Slide Show, apply concepts of linear functions to the context of distance vs. time data and graphs. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
Instructional Resource: Applications of Linear Functions: Hooke's Law	In this Slide Show, apply concepts of linear functions to the context of Hooke's law. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions and Proportions
Instructional Resource: Applications of Linear Functions: Momentum and Impulse	In this Slide Show, apply concepts of linear functions to the context of momentum and impulse. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
Instructional Resource: Applications of Linear Functions: Perimeter of a Rectangle	In this Slide Show, apply concepts of linear functions to the context of rectangular perimeter. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
Instructional Resource: Applications of Linear Functions: Saving Money	In this Slide Show, apply concepts of linear functions to the context of saving money. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
Instructional Resource: Applications of Linear Functions: Speed and acceleration	In this Slide Show, apply concepts of linear functions to the context of speed and acceleration. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
Instructional Resource: Applications of Linear Functions: Temperature Conversion	In this Slide Show, apply concepts of linear functions to the context of converting Celsius and Fahrenheit temperatures. Note: The download is a PPT file. Related Resources To see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN	Applications of Linear Functions
INSTRUCTIONAL RESOURCE: Desmos Tutorial: Linear Functions in Slope Intercept Form	INSTRUCTIONAL RESOURCE: Desmos Tutorial: Linear Functions in Slope Intercept Form In this Slide Show, use the Desmos graphing calculator to explore linear equations in slope intercept form. To see the complete collection of Desmos Resources click on this link. Note: The download is a PPT file. This is part of a collection of Desmos tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Graphs of Linear Functions and Slope-Intercept Form