
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 21: Cylinders, Cones, and Spheres
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
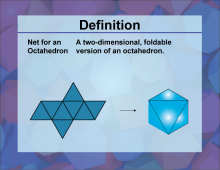
Definition--3D Geometry Concepts--Net for an Octahedron | Net for an OctahedronTopic3D Geometry DefinitionA net for an octahedron is a two-dimensional figure that can be folded to form a three-dimensional octahedron. DescriptionIn the realm of three-dimensional geometry, a net is a crucial concept that helps in visualizing and constructing 3D shapes from 2D representations. Specifically, a net for an octahedron consists of eight equilateral triangles arranged in a specific pattern. When these triangles are folded along the edges, they form an octahedron, which is a polyhedron with eight faces, twelve edges, and six vertices. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Platonic Solids | Platonic SolidsTopic3D Geometry DefinitionA Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space, where each face is a congruent regular polygon, and the same number of faces meet at each vertex. DescriptionPlatonic solids are fundamental constructs in the study of three-dimensional geometry. These solids are unique because they are the only five regular polyhedra that exist. Each Platonic solid has faces that are congruent regular polygons, and the same number of faces meet at each vertex, making them highly symmetrical and aesthetically pleasing. The five Platonic solids are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, each named for its number of faces. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Prism | PrismTopic3D Geometry DefinitionA prism is a three-dimensional solid object with two identical polygonal bases connected by parallelogram faces. DescriptionIn the realm of three-dimensional geometry, a prism is a polyhedron with two parallel, congruent bases connected by rectangular or parallelogram faces. The defining characteristic of a prism is that its cross-sections parallel to the bases are identical to the bases themselves. This property makes prisms a significant topic of study in geometry. |
3-Dimensional Figures |
|
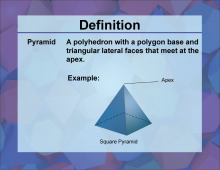
Definition--3D Geometry Concepts--Pyramid | PyramidTopic3D Geometry DefinitionA pyramid is a three-dimensional geometric figure with a polygonal base and triangular faces that converge to a single point called the apex. DescriptionIn the realm of three-dimensional geometry, a pyramid is a significant shape due to its unique properties and applications. A pyramid consists of a base that can be any polygon, such as a triangle, square, or pentagon, and triangular faces that connect each edge of the base to a single apex point. This structure results in a solid figure that is both aesthetically pleasing and structurally efficient. |
Pyramids |
|
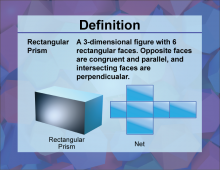
Definition--3D Geometry Concepts--Rectangular Prism | Rectangular PrismTopic3D Geometry DefinitionA rectangular prism is a three-dimensional figure with six rectangular faces, where opposite faces are congruent and parallel. DescriptionThe rectangular prism is a fundamental shape in three-dimensional geometry, serving as a building block for understanding more complex 3D structures. It is characterized by its three dimensions: length, width, and height, which are clearly labeled in the image. This shape is ubiquitous in both natural and man-made environments, making it a crucial concept for students to grasp. |
Rectangular Prisms |
|
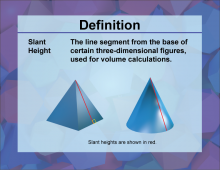
Definition--3D Geometry Concepts--Slant Height | Slant HeightTopic3D Geometry DefinitionSlant height is the distance measured along a lateral face from the base to the apex of a three-dimensional figure, such as a pyramid or a cone. DescriptionIn the context of three-dimensional geometry, the slant height is a crucial measurement for various solid figures, particularly right pyramids and right circular cones. It represents the shortest path along the surface of the figure from the apex (top point) to the base, distinguishing it from the vertical height which measures the perpendicular distance from the apex to the center of the base. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Sphere | SphereTopic3D Geometry DefinitionA sphere is a perfectly round three-dimensional geometric object in which every point on the surface is equidistant from the center. DescriptionIn the realm of three-dimensional geometry, a sphere is a fundamental shape characterized by its symmetry and uniformity. It is defined mathematically as the set of all points in space that are at a constant distance, known as the radius, from a fixed point called the center. This distance is the same in all directions, making the sphere a unique object with no edges or vertices. |
Spheres |
|
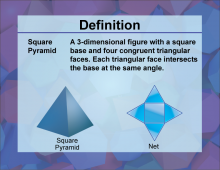
Definition--3D Geometry Concepts--Square Pyramid | Square PyramidTopic3D Geometry DefinitionA square pyramid is a three-dimensional geometric figure with a square base and four triangular faces that converge at a single point called the apex. |
Pyramids |

|
Definition--3D Geometry Concepts--Surface Area | Surface Area of 3D FiguresTopic3D Geometry DefinitionSurface area is the total area that the surface of a three-dimensional object occupies. DescriptionIn the realm of three-dimensional geometry, surface area is a fundamental concept that quantifies the extent of a 3D shape's exterior surface. This measure is crucial for various applications, including engineering, architecture, and everyday tasks. For example, when painting a room, the surface area of the walls, ceiling, and floor must be calculated to determine the amount of paint required. |
Surface Area |
|
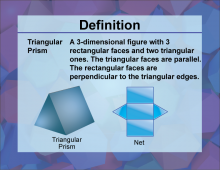
Definition--3D Geometry Concepts--Triangular Prism | Triangular PrismTopic3D Geometry DefinitionA triangular prism is a three-dimensional geometric solid with two congruent triangular bases and three rectangular faces. DescriptionThe triangular prism is a fundamental shape in three-dimensional geometry, playing a crucial role in understanding the properties of polyhedra and their applications in various fields. This prism is characterized by its unique structure, consisting of two parallel triangular bases connected by three rectangular faces. The shape of the triangular bases can vary, allowing for right, equilateral, isosceles, or scalene triangular prisms. |
Triangular Prisms |
|
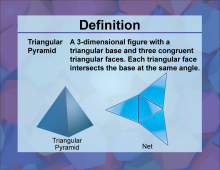
Definition--3D Geometry Concepts--Triangular Pyramid | Triangular PyramidTopic3D Geometry DefinitionA triangular pyramid, also known as a tetrahedron, is a three-dimensional geometric figure with four triangular faces, six edges, and four vertices. DescriptionIn the realm of three-dimensional geometry, the triangular pyramid holds significant relevance due to its unique properties and structural simplicity. Each triangular face of the pyramid converges at a single point known as the apex, forming a solid figure that is both symmetrical and aesthetically pleasing. This geometric shape is the simplest form of a pyramid and is often used in various fields such as architecture, molecular chemistry, and computer graphics. |
Pyramids |
|
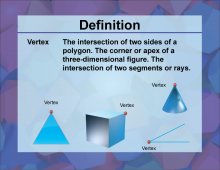
Definition--3D Geometry Concepts--Vertex | Vertex in 3D GeometryTopic3D Geometry DefinitionA vertex is a point where three or more edges meet in a three-dimensional figure. DescriptionIn the study of three-dimensional geometry, the term vertex is fundamental. A vertex is a critical point in any 3D geometric shape, marking the intersection of edges. For example, in a cube, each corner where the edges converge is a vertex. Vertices are essential in defining the shape and structure of 3D figures, as they help in understanding the spatial relationships between different parts of the figure. |
3-Dimensional Figures |
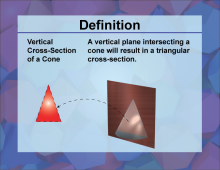
|
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Cone | Vertical Cross Sections of a ConeTopic3D Geometry DefinitionA vertical cross section of a cone is the intersection of the cone with a plane that passes through its vertex and base, resulting in a two-dimensional shape. |
Cones |
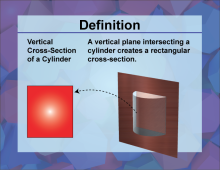
|
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Cylinder | Vertical Cross Sections of a CylinderTopic3D Geometry DefinitionA vertical cross-section of a cylinder is the intersection of the cylinder with a plane that is parallel to its axis. This cross-section is typically a rectangle if the plane cuts through the entire height of the cylinder. |
Cylinders |
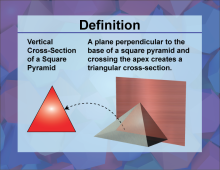
|
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Square Pyramid | Vertical Cross Sections of a Square PyramidTopic3D Geometry DefinitionA vertical cross section of a square pyramid is the intersection of the pyramid with a vertical plane that passes through its apex and base, resulting in a two-dimensional shape. |
Pyramids |
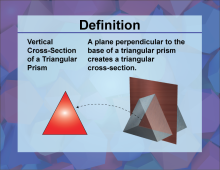
|
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Triangular Prism | Vertical Cross Sections of a Triangular PrismTopic3D Geometry DefinitionA vertical cross section of a triangular prism is a two-dimensional shape obtained by slicing the prism parallel to its height, revealing a triangular face. |
Triangular Prisms |

|
Definition--3D Geometry Concepts--Volume | VolumeTopic3D Geometry DefinitionVolume is the measure of the amount of space occupied by a three-dimensional object, expressed in cubic units. DescriptionVolume is a fundamental concept in the study of three-dimensional geometry. It quantifies the capacity of a 3D object, indicating how much space it occupies. This measurement is crucial in various fields, including mathematics, engineering, architecture, and physical sciences. |
Volume |
|
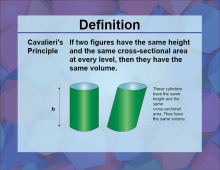
Definition--3D Geometry Concepts--Cavalieri's Principle | Cavalieri's PrincipleTopic3D Geometry DefinitionCavalieri's Principle states that if two solids are contained between two parallel planes, and every plane parallel to these planes intersects both solids in cross-sections of equal area, then the two solids have equal volumes. DescriptionCavalieri's Principle is a fundamental concept in three-dimensional geometry that provides a method for determining the volume of solids. Named after the Italian mathematician Bonaventura Cavalieri, this principle is particularly useful for comparing the volumes of solids that might not have straightforward geometric shapes. |
3-Dimensional Figures |

|
Geometry Applications Teachers Guide: 3D Geometry | Geometry Applications Teachers Guide: 3D Geometry
This is the Teacher's Guide that accompanies Geometry Applications: 3D Geometry. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of 3D Geometry |

|
Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2 | Google Earth Voyager Story: The Geometry of Sustainable Architecture, Part 2TopicGeometric Models |
Surface Area, Volume and Rational Functions and Equations |

|
Google Earth Voyager Story: The Mathematics of Pyramids, Part 1 | Google Earth Voyager Story: The Mathematics of Pyramids, Part 1TopicGeometric Models |
Pyramids |

|
Google Earth Voyager Story: The Mathematics of Pyramids, Part 2 | Google Earth Voyager Story: The Mathematics of Pyramids, Part 2TopicGeometric Models |
Pyramids |

|
INSTRUCTIONAL RESOURCE: Math Examples 55 | INSTRUCTIONAL RESOURCE: Math Examples--Surface Area
This set of tutorials provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Surface Area |

|
Interactive Math Game--Memory Game: 3D Figures | Interactive Math Game--Memory Game: 3D Figures
Use this math game to review 3D figures. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
3-Dimensional Figures |

|
Interactive Math Game: Math Riddles--3D Geometry | Interactive Math Game: Math Riddles--3D Geometry
In this Math Riddles Game, have your students review vocabulary around the topic of 3D Geometry. The Math Riddles games are useful for practicing: Math Vocabulary, Key Concepts, Critical Thinking. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
3-Dimensional Figures |

|
Lesson Plan: Cross-Sections of 3D Figures, Part 1 | Lesson Plan: Cross-Sections of 3D Figures In this engaging math lesson, students explore cross-sections of cubes, cylinders, and cones through interactive activities, real-world examples, and animated visuals. They will learn how slicing three-dimensional shapes in different ways produces a variety of two-dimensional figures, helping to develop spatial reasoning and geometric understanding. The lesson begins with a conceptual introduction to cross-sections, followed by hands-on practice with everyday objects such as gift boxes, paper towel rolls, and ice cream cones. Students will investigate how horizontal, vertical, and diagonal slices impact the resulting shapes. Animated GIFs illustrate these concepts, reinforcing learning through dynamic visual representations. |
3-Dimensional Figures |

|
Lesson Plan: Cross-Sections of 3D Figures, Part 2 | Lesson Plan: Cross-Sections of Rectangular Prisms, Spheres, and Pyramids In this engaging geometry lesson, students will explore how rectangular prisms, spheres, and pyramids are affected by different slicing planes. Using visual aids, real-world examples, and hands-on activities, students will identify the cross-sections created by horizontal, vertical, and diagonal cuts. Through interactive exploration, students will learn that a rectangular prism produces rectangular or parallelogram cross-sections, a sphere always results in a circular cross-section regardless of the slicing direction, and a pyramid creates triangles, trapezoids, or smaller versions of its base. The lesson also introduces the volume formula for a rectangular prism, reinforcing the connection between cross-sections and three-dimensional measurements. |
Applications of 3D Geometry |

|
Lesson Plan: Nets of 3D Figures, Part 1 | Lesson Plan: Introduction to Nets and Basic 3D Shapes In this engaging and interactive lesson, students explore the connection between 2D nets and 3D geometric figures. Through animations, printable foldable nets, and hands-on activities, students will develop a deeper understanding of how nets transform into solid figures such as cubes, rectangular prisms, and triangular prisms. This lesson also reinforces key geometry concepts, including faces, edges, and vertices, while guiding students through surface area calculations using nets. |
3-Dimensional Figures |
|
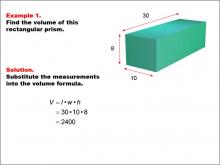
Math Example--Volume Concepts--Calculating Volume: Example 1 | Math Example--Volume Concepts--Calculating Volume: Example 1TopicVolume DescriptionA rectangular prism with dimensions labeled: length = 30, width = 10, and height = 8. The image shows how to find the volume of the prism using the formula for volume of a rectangular prism. This image illustrates Example 1: The caption explains how to calculate the volume of the rectangular prism using the formula V = l * w * h. The given dimensions are substituted into the formula: V = 30 * 10 * 8 = 2400.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
|
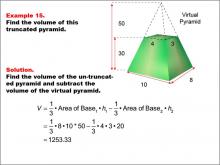
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
|
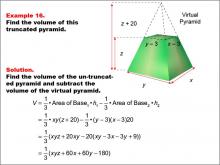
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 17 | Math Example--Volume Concepts--Calculating Volume: Example 17TopicVolume DescriptionA green sphere with a radius labeled as 3. The image is part of a math example showing how to calculate the volume of a sphere. This image illustrates Example 17: The text describes finding the volume of a sphere. The formula used is V = (4/3) * π * r3, where r = 3. After substituting, the result is V = 36π. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 18 | Math Example--Volume Concepts--Calculating Volume: Example 18TopicVolume Description
A green sphere with a radius labeled as x. This image is part of a math example showing how to calculate the volume of a sphere using an unknown radius. This image illustrates Example 18: The text explains how to find the volume of a sphere with an unknown radius x. The formula used is V = (4/3) * π * r3, and substituting r = x gives V = (4/3) * x3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 19 | Math Example--Volume Concepts--Calculating Volume: Example 19TopicVolume Description
A green cube with side length labeled as 7. The image illustrates how to calculate the volume of a cube with known side length. This image illustrates Example 19: The text describes finding the volume of a cube. The formula used is V = s3, where s = 7. After substituting, the result is V = 343. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |
|
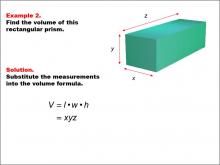
Math Example--Volume Concepts--Calculating Volume: Example 2 | Math Example--Volume Concepts--Calculating Volume: Example 2TopicVolume DescriptionA rectangular prism with dimensions labeled as x, y, and z. The image shows a general example of calculating the volume of a rectangular prism using variables instead of specific numbers. This image illustrates Example 2: The caption describes how to find the volume of a rectangular prism using variables for length (x), width (y), and height (z). The formula is given as V = x * y * z, but no specific values are provided. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 20 | Math Example--Volume Concepts--Calculating Volume: Example 20TopicVolume DescriptionA green cube with side length labeled as x. This image is part of a math example showing how to calculate the volume of a cube using an unknown side length. This image illustrates Example 20: The text explains how to find the volume of a cube with an unknown side length x. The formula used is V = s3, and substituting s = x gives V = x3. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 21 | Math Example--Volume Concepts--Calculating Volume: Example 21TopicVolume DescriptionA hollow cube with an outer edge of 9 and an inner hollow region with an edge of 7. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 21: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 is the outer edge (9) and s2 is the inner edge (7). The solution calculates 9^3 - 7^3 = 386.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 22 | Math Example--Volume Concepts--Calculating Volume: Example 22TopicVolume DescriptionA hollow cube with an outer edge of x and an inner hollow region with an edge of x - 2. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 22: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 = x and s2 = x - 2. Expanding and simplifying gives V = 6x2 - 12x + 8. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 23 | Math Example--Volume Concepts--Calculating Volume: Example 23TopicVolume Description
A cone with a height of 12 and a radius of 4. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 23: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = 4 and h = 12. Substituting these values gives V = (1/3) * π * (42) * 12 = 64π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 24 | Math Example--Volume Concepts--Calculating Volume: Example 24TopicVolume DescriptionA cone with a height labeled as y and a radius labeled as x. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 24: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = x and h = y. Substituting these variables gives V = (x^2 * y)/3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 3 | Math Example--Volume Concepts--Calculating Volume: Example 3TopicVolume DescriptionA hollow rectangular prism with outer dimensions: length = 60, width = 20, and height = 16. The inner hollow part has dimensions: length = 60, width = 18, and height = 14. The image shows how to subtract volumes to find the hollow volume. This image illustrates Example 3: The caption explains how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume. V = (60 * 20 * 16) - (60 * 18 * 14) = 4080. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 4 | Math Example--Volume Concepts--Calculating Volume: Example 4TopicVolume DescriptionA hollow rectangular prism with outer dimensions labeled as x, y, and z, and inner hollow dimensions labeled as x - 2 and y - 2. The image shows a symbolic calculation for finding the hollow volume using variables. This image illustrates Example 4: The caption describes how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume using variables: V = xyz - z(y - 2)(x - 2) = 2z(y + x - 2). |
Volume |
|
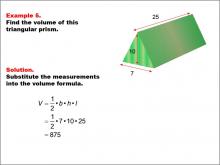
Math Example--Volume Concepts--Calculating Volume: Example 5 | Math Example--Volume Concepts--Calculating Volume: Example 5TopicVolume DescriptionThe image shows a triangular prism with dimensions labeled as base (7), height (10), and length (25). It is part of an example on how to calculate the volume of a solid triangular prism. This image illustrates Example 5: "Find the volume of this triangular prism." The solution involves substituting the given measurements into the volume formula for a triangular prism: V = 1/2 * b * h * l = 1/2 * 7 * 10 * 25 = 875. |
Volume |
|
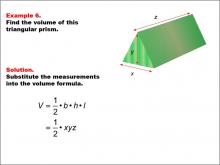
Math Example--Volume Concepts--Calculating Volume: Example 6 | Math Example--Volume Concepts--Calculating Volume: Example 6TopicVolume DescriptionThe image depicts a triangular prism with dimensions labeled as x, y, and z. The example demonstrates how to calculate the volume using a general formula for a triangular prism. This image illustrates Example 6: "Find the volume of this triangular prism." The solution uses the formula V = 1/2 * b * h * l, which is simplified to V = 1/2 * x * y * z.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 7 | Math Example--Volume Concepts--Calculating Volume: Example 7TopicVolume DescriptionThe image shows a hollow triangular prism with outer dimensions labeled as base (10), height (7), and length (35), and inner dimensions labeled as base (8) and height (5). The example calculates the volume by subtracting the hollow region from the full prism. This image illustrates Example 7: "Find the volume of this hollow triangular prism." The solution calculates the full volume using V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = 1/2 * 10 * 7 * 35 - 1/2 * 8 * 5 * 35 = 525.. |
Volume |