Illustrative Math Alignment: Grade 8 Unit 6

Topic

Sequences and Series

Definition

The binomial theorem describes the algebraic expansion of powers of a binomial.

Description

The binomial theorem is a fundamental theorem in algebra that provides a formula for expanding binomials raised to any positive integer power. This theorem is essential in various mathematical disciplines, including algebra, calculus, and probability theory.

Topic

Sequences and Series

Definition

The common difference is the difference between consecutive terms in an arithmetic sequence.

Description

The common difference is a key concept in arithmetic sequences, representing the consistent interval between consecutive terms. This concept is fundamental in understanding linear patterns and is widely used in various mathematical applications.

Topic

Sequences and Series

Definition

The common ratio is the ratio between consecutive terms in a geometric sequence.

Description

The common ratio is a fundamental concept in geometric sequences, representing the consistent factor by which each term is multiplied to obtain the next term. This concept is crucial in understanding exponential growth and decay, which are prevalent in various mathematical and scientific applications.

Topic

Sequences and Series

Definition

A convergent series is a series whose terms approach a specific value as the number of terms increases.

Description

A convergent series is a critical concept in the study of sequences and series, where the sum of its terms approaches a finite limit as the number of terms increases. This concept is essential in various mathematical and scientific applications, including calculus and analysis.

Topic

Sequences and Series

Definition

A divergent series is a series whose terms do not approach a specific value as the number of terms increases.

Description

A divergent series is a significant concept in the study of sequences and series, where the sum of its terms does not approach a finite limit as the number of terms increases. This concept is essential in various mathematical and scientific applications, including calculus and analysis.

Topic

Sequences and Series

Definition

An explicit formula for a sequence provides a direct way to calculate any term in the sequence.

Description

An explicit formula for a sequence is a mathematical expression that allows for the direct computation of any term in the sequence without needing to know the previous terms. This concept is fundamental in the study of sequences and series and is widely used in various mathematical applications.

Topic

Sequences and Series

Definition

The Fibonacci sequence is a sequence where each term is the sum of the two preceding ones, starting from 0 and 1.

Description

The Fibonacci sequence is a famous sequence in mathematics, where each term is the sum of the two preceding ones, starting from 0 and 1. This sequence is significant in various mathematical and scientific applications, including computer science, biology, and art.

Topic

Sequences and Series

Definition

A finite sequence is a sequence that has a limited number of terms.

Description

A finite sequence is a sequence with a specific number of terms, making it a crucial concept in the study of sequences and series. This concept is fundamental in various mathematical applications where the number of elements is limited, such as in statistics and computer science.

In real-world applications, finite sequences are used in data analysis, where datasets have a specific number of entries. They are also used in computer algorithms that process a fixed number of elements. Algebraically, a finite sequence can be represented as

Topic

Sequences and Series

Definition

A finite series is the sum of the terms of a finite sequence.

Description

A finite series is a significant concept in mathematics, representing the sum of the terms of a finite sequence. This concept is essential in various mathematical and scientific applications, including statistics, finance, and computer science.

In real-world applications, finite series are used in financial calculations, such as determining the total amount of payments over a fixed period. They are also used in data analysis to find the sum of a dataset. Algebraically, a finite series can be expressed as  

Topic

Sequences and Series

Definition

A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio.

Description

A geometric sequence is a fundamental concept in mathematics, particularly in the study of sequences and series. It is defined by the property that each term after the first is the product of the previous term and a constant, known as the common ratio. This concept is crucial in various mathematical applications, including exponential growth and decay.

Topic

Sequences and Series

Definition

A geometric series is the sum of the terms of a geometric sequence.

Description

A geometric series is a significant concept in mathematics, especially in the study of sequences and series. It is formed by adding the terms of a geometric sequence. This concept is crucial for understanding how sums of exponential patterns are calculated, which has applications in various fields such as finance, engineering, and computer science.

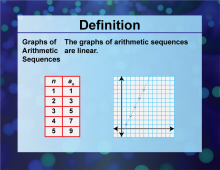
Topic

Sequences and Series

Definition

Graphs of arithmetic sequences form a linear graph on a coordinate plane.

Description

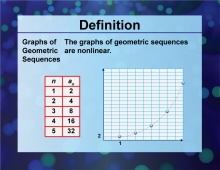
Graphs of arithmetic sequences are a visual tool used in mathematics to represent the terms of an arithmetic sequence on a coordinate plane. This concept is crucial for understanding linear patterns and relationships in sequences and series.

Topic

Sequences and Series

Definition

Graphs of geometric sequences visually represent the terms of a geometric sequence on a coordinate plane. These are nonlinear graphs.

Description

Graphs of geometric sequences are a visual tool used in mathematics to represent the terms of a geometric sequence on a coordinate plane. This concept is crucial for understanding exponential patterns and relationships in sequences and series.

Topic

Sequences and Series

Definition

An infinite sequence is a sequence that continues indefinitely without terminating.

Description

An infinite sequence is a fundamental concept in mathematics, representing a sequence that continues indefinitely without terminating. This concept is essential in various mathematical and scientific applications, including calculus and analysis.

In real-world applications, infinite sequences are used in mathematical modeling and simulations where processes continue indefinitely, such as in population dynamics or financial forecasting. Algebraically, an infinite sequence can be represented as  

Topic

Sequences and Series

Definition

An infinite series is the sum of the terms of an infinite sequence.

Description

An infinite series is a significant concept in mathematics, representing the sum of the terms of an infinite sequence. This concept is essential in various mathematical and scientific applications, including calculus and analysis.

In real-world applications, infinite series are used in mathematical modeling and simulations where processes continue indefinitely, such as in signal processing or financial forecasting. Algebraically, an infinite series can be represented as 

Topic

Sequences and Series

Definition

Pascal's Triangle is a triangular array of binomial coefficients.

Description

Pascal's Triangle is a fundamental concept in mathematics, representing a triangular array of binomial coefficients. This concept is essential in various mathematical and scientific applications, including combinatorics, algebra, and probability theory.

In real-world applications, Pascal's Triangle is used in probability calculations, particularly in binomial expansions and combinatorial problems. It is also used in computer science for algorithm design. Algebraically, the elements of Pascal's Triangle can be expressed as  

Topic

Sequences and Series

Definition

A recursive formula defines each term of a sequence using the preceding term(s).

Description

A recursive formula is a fundamental concept in mathematics, representing a way to define each term of a sequence using the preceding term(s). This concept is essential in various mathematical and scientific applications, including computer science and algorithm design.

Topic

Sequences and Series

Definition

A sequence is an ordered list of numbers that follow a particular pattern or rule.

Description

Sequences are fundamental concepts in mathematics, representing ordered lists of numbers that follow a specific pattern or rule. This concept is crucial in various mathematical applications, including algebra, calculus, and computer science.

Topic

Sequences and Series

Definition

A series is the sum of the terms of a sequence.

Description

Series are significant concepts in mathematics, representing the sum of the terms of a sequence. This concept is essential in various mathematical and scientific applications, including calculus, analysis, and financial modeling.

In real-world applications, series are used in financial calculations, such as determining the total amount of payments or investments over time. They are also used in data analysis to find the sum of a dataset. Algebraically, series can be represented in various forms, such as arithmetic series, geometric series, and more.

Topic

Sequences and Series

Definition

Square numbers are numbers that are the square of an integer.

Description

Square numbers are fundamental concepts in mathematics, representing numbers that are the square of an integer. This concept is crucial in various mathematical applications, including algebra, geometry, and number theory.

In real-world applications, square numbers are used in area calculations, particularly in determining the area of squares. They are also used in computer algorithms and cryptography. Algebraically, square numbers can be represented as n2 , where n is an integer.

Topic

Sequences and Series

Definition

Summation notation is a mathematical notation used to represent the sum of a sequence of terms.

Description

Summation notation is a powerful tool in mathematics, representing the sum of a sequence of terms in a compact form. This concept is essential in various mathematical and scientific applications, including calculus, statistics, and computer science.

Topic

Sequences and Series

Definition

Triangular numbers are numbers that can be represented by an equilateral triangle.

Description

Triangular numbers are fundamental concepts in mathematics, representing numbers that can form an equilateral triangle. This concept is crucial in various mathematical applications, including algebra, geometry, and number theory.

In real-world applications, triangular numbers are used in combinatorial problems and in determining the number of connections in a network. They are also used in computer algorithms and game design. Algebraically, triangular numbers can be represented as  

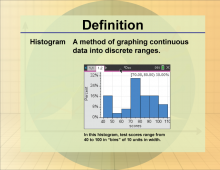
Topic

Statistics and Probability

Definition

A histogram is a graphical representation of data distribution using bars of different heights.

Description

Histograms are a fundamental tool in statistics for visualizing the frequency distribution of a dataset. They are used across various fields, including economics, biology, and engineering, to analyze data patterns and trends. By displaying data in intervals, histograms help identify the shape, central tendency, and variability of data. For students, understanding histograms is crucial for interpreting data visually and making informed decisions based on statistical evidence.

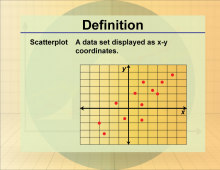
Topic

Statistics and Probability

Definition

A scatterplot is a graphical representation of the relationship between two numerical variables.

Description

Scatterplots are essential tools in statistics for visualizing the correlation between two variables. They are widely used in fields like economics and biology to identify trends and relationships in data.

For students, understanding scatterplots is important for interpreting data visually and analyzing the strength and direction of relationships between variables. This skill is crucial for developing their ability to conduct statistical analyses and draw meaningful conclusions from data.

Topic

Statistics and Probability

Definition

A stem-and-leaf plot is a graphical representation that organizes data points based on their place value.

Description

Stem-and-leaf plots are useful for displaying the distribution of a dataset in a concise format, preserving the original data while showing its shape. They are particularly helpful in exploratory data analysis to identify patterns and outliers.

In educational settings, stem-and-leaf plots are used to teach students about data organization and visualization. Understanding this concept helps students develop skills in data interpretation and enhances their ability to summarize data effectively.

The formula for the Median.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

The formula for the Sum of Consecutive Integers.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

The formula for the Sum of Consecutive Integers.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

In this interactive, review seven commonly used data displays. Provides a quck review tool for a unit on data analysis. Note: the download is the Teacher's Guide.

Related Resources

In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions.

In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money.

In this Slide Show, apply concepts of linear functions to the context of circumference vs. diameter.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of cost vs. time data and graphs.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of cricket chirps.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of distance vs. time data and graphs.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of Hooke's law.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of momentum and impulse.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of rectangular perimeter.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of saving money.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of speed and acceleration.

Note: The download is a PPT file.

Related Resources

In this Slide Show, apply concepts of linear functions to the context of converting Celsius and Fahrenheit temperatures.

Note: The download is a PPT file.

Related Resources

In this Slide Show, learn how graph data in a scatterplot using the graph window. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT.

In this tutorial we walk students through the steps of doing a quadratic regression on a Desmos graphing calculator. The steps include showing how to create pseudo-quadratic data on a spreadsheet.

Library of Instructional Resources

To see the complete library of Instructional Resources , click on this link. 

Solve an interactive word search puzzle on the topic of Data Analysis.

Related Resources

Solve an interactive word search puzzle on the topic of Data Analysis.

Related Resources

Solve an interactive word search puzzle on the topic of Data Analysis.

Related Resources

Solve an interactive word search puzzle on the topic of Data Analysis.

Related Resources

Solve an interactive word search puzzle on the topic of Data Analysis.

Related Resources

Topic

Probability and Statistics

Description

This image depicts a spinner divided into ten equal sections, which are colored red, yellow, green, light blue, orange, grey, brown, purple, yellow-green, and white. The spinner's arrow points to the red section, demonstrating one of the possible outcomes.

In the context of Probability and Statistics, this spinner represents a probability experiment with ten equally likely outcomes. It visually demonstrates the concepts of sample space and individual events within that space, each with a 1/10 probability of occurrence.

Topic

Probability and Statistics

Description

This image depicts a spinner divided into ten equal sections, which are colored red, yellow, green, light blue, orange, grey, brown, purple, yellow-green, and white. The spinner's arrow points to the white section, demonstrating the final possible outcome in this probability model.

In the field of Probability and Statistics, this spinner exemplifies a uniform probability distribution with ten equally likely outcomes. Each spin has a 1/10 probability of landing on any given color, illustrating the concept of equiprobable events in a complex scenario.