Illustrative Math Alignment: Grade 8 Unit 6

Associations in Data

Lesson 11: Gone In 30 Seconds

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
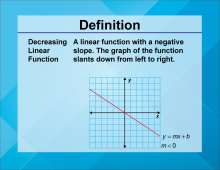
Definition--Linear Function Concepts--Decreasing Linear Function	Decreasing Linear Function Topic Linear Functions Definition A decreasing linear function is a linear function where the slope is negative, indicating that as the input value increases, the output value decreases. Description Decreasing linear functions are important in understanding how variables inversely relate to each other. The negative slope signifies a reduction in the dependent variable as the independent variable increases. Real-world examples include depreciation of assets over time or the decrease in temperature as altitude increases. These functions help model scenarios where an increase in one quantity results in a decrease in another.	Slope-Intercept Form
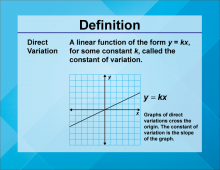
Definition--Linear Function Concepts--Direct Variation	Direct Variation Topic Linear Functions Definition Direct variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. Description Direct variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering.	Slope-Intercept Form
Definition--Linear Function Concepts--Equations of Parallel Lines	Equations of Parallel Lines Topic Linear Functions Definition Equations of parallel lines are linear equations that have the same slope but different y-intercepts, indicating that the lines never intersect. Description Understanding equations of parallel lines is crucial in geometry and algebra. Parallel lines have identical slopes, which means they run in the same direction and never meet. In real-world applications, parallel lines can model scenarios such as railway tracks or lanes on a highway, where maintaining a consistent distance is essential.	Slope-Intercept Form
Definition--Linear Function Concepts--Equations of Perpendicular Lines	Equations of Perpendicular Lines Topic Linear Functions Definition Equations of perpendicular lines are linear equations where the slopes are negative reciprocals of each other, indicating that the lines intersect at a right angle. Description Equations of perpendicular lines are significant in both geometry and algebra. The negative reciprocal relationship between their slopes ensures that the lines intersect at a 90-degree angle. In real-world applications, perpendicular lines are found in various structures, such as the intersection of streets or the corners of a building, where right angles are essential.	Slope-Intercept Form
Definition--Linear Function Concepts--Identity Function	Identity Function Topic Linear Functions Definition An identity function is a linear function of the form f(x) = x, where the output is equal to the input for all values of x. Description The identity function is a basic yet crucial concept in linear functions. It represents a scenario where the input value is always equal to the output value, graphically depicted as a 45-degree line passing through the origin. In real-world applications, the identity function can model situations where input and output are directly proportional and identical, such as converting units of the same measure. This also introduces the concept of identity, which is fundamental to mathematics.	Slope-Intercept Form
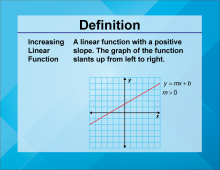
Definition--Linear Function Concepts--Increasing Linear Function	Increasing Linear Function Topic Linear Functions Definition An increasing linear function is a linear function where the slope is positive, indicating that as the input value increases, the output value also increases. Description Increasing linear functions are essential in understanding how variables positively relate to each other. The positive slope signifies an increase in the dependent variable as the independent variable increases. Real-world examples include income increasing with hours worked or the rise in temperature with the increase in daylight hours. These functions help model scenarios where an increase in one quantity results in an increase in another.	Slope-Intercept Form
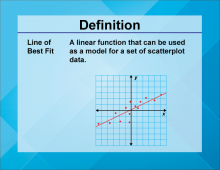
Definition--Linear Function Concepts--Line of Best Fit	Line of Best Fit Topic Linear Functions Definition A line of best fit is a straight line that best represents the data on a scatter plot, showing the trend of the data points. Description The line of best fit is a crucial concept in statistics and data analysis. It helps in identifying the trend and making predictions based on the data. In real-world applications, the line of best fit is used in various fields such as economics, biology, and engineering to analyze trends and make forecasts. For example, it can be used to predict future sales based on past data.	Graphs of Linear Functions
Definition--Linear Function Concepts--Linear Equations in Standard Form	Linear Equations in Standard Form Topic Linear Functions Definition Linear equations in standard form are written as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. Description Linear equations in standard form are a fundamental representation of linear functions. They provide a way to express linear relationships in a general form.	Standard Form
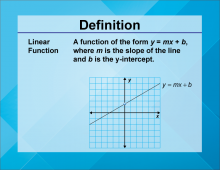
Definition--Linear Function Concepts--Linear Function	Linear Function Topic Linear Functions Definition A linear function is a function that can be graphed as a straight line, typically written in the form y = mx + b, where m is the slope and b is the y-intercept. Description Linear functions are one of the most fundamental concepts in mathematics. They describe relationships where the rate of change between variables is constant, represented graphically as a straight line. This simplicity makes them a central topic in algebra and calculus.	Slope-Intercept Form
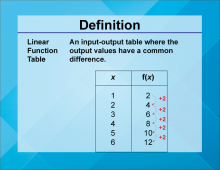
Definition--Linear Function Concepts--Linear Function Tables	Linear Function Tables Topic Linear Functions Definition Linear function tables display the input-output pairs of a linear function, showing how the dependent variable changes with the independent variable. Description Linear function tables are useful tools for understanding and analyzing linear relationships. They provide a clear way to see how changes in the input (independent variable) affect the output (dependent variable).	Applications of Linear Functions and Graphs of Linear Functions
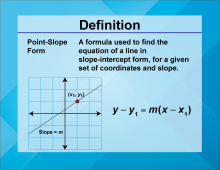
Definition--Linear Function Concepts--Point-Slope Form	Point-Slope Form Topic Linear Functions Definition Point-slope form of a linear equation is written as y − y1 = m(x−x1 ), where m is the slope and (x1 ,y1) is a point on the line. Description The point-slope form is a versatile way to express linear equations, especially useful when you know a point on the line and the slope. It allows for quick construction of the equation of a line.	Point-Slope Form
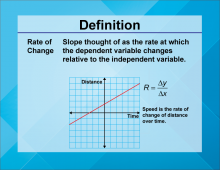
Definition--Linear Function Concepts--Rate of Change	Rate of Change Topic Linear Functions Definition Rate of change in a linear function is the ratio of the change in the dependent variable to the change in the independent variable, often represented as the slope m in the equation y = mx + b. Description Rate of change is a fundamental concept in understanding linear functions. It describes how one variable changes in relation to another, and is graphically represented by the slope of a line.	Slope
Definition--Linear Function Concepts--Slope-Intercept Form	Slope-Intercept Form Topic Linear Functions Definition Slope-intercept form of a linear equation is written as y = mx + b, where m is the slope and b is the y-intercept. Description Slope-intercept form is one of the most commonly used forms of linear equations. It provides a clear way to understand the slope and y-intercept of a line, making it easier to graph and interpret. In real-world applications, slope-intercept form is used in various fields such as economics, physics, and engineering to model linear relationships. For example, it can represent the relationship between cost and production levels in business.	Slope-Intercept Form
Definition--Linear Function Concepts--The Equation of a Line From Two Coordinates	The Equation of a Line From Two Coordinates Topic Linear Functions Definition The equation of a line from two coordinates can be determined by finding the slope between the two points and using it in the point-slope form of a linear equation. Description Finding the equation of a line from two coordinates is a fundamental skill in algebra. It involves calculating the slope between the two points and then using one of the points to form the equation in point-slope or slope-intercept form.	Point-Slope Form
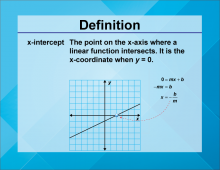
Definition--Linear Function Concepts--x-Intercept	x-Intercept Topic Linear Functions Definition The x-intercept is the point where a graph crosses the x-axis, indicating the value of x when 𝑦 y is zero. Description The x-intercept is a key concept in understanding the behavior of linear functions. It represents the point where the function's output is zero, providing insight into the function's roots and behavior. In real-world applications, the x-intercept can be used to determine break-even points in business, where revenue equals costs, or to find the time at which a process starts or stops.	Slope-Intercept Form
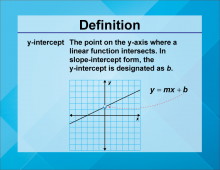
Definition--Linear Function Concepts--y-Intercept	y-Intercept Topic Linear Functions Definition The y-intercept is the point where a graph crosses the y-axis, indicating the value of y when x is zero. Description The y-intercept is a fundamental concept in understanding the behavior of linear functions. It represents the initial value of the function when the input is zero, providing insight into the function's starting point. In real-world applications, the y-intercept can be used to determine initial conditions in various scenarios, such as the starting balance in a bank account or the initial position of an object in motion.	Slope-Intercept Form
Definition--Measures of Central Tendency	Measures of Central Tendency Topic Statistics Definition The measures of central tendency is a measure of central tendency that provides an average representation of a set of data. Description The Measures of Central Tendency is an important concept in statistics, used to summarize data effectively. In real-world applications, the Measures of Central Tendency helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5.	Data Analysis
Definition--Measures of Central Tendency--Average	Average Topic Statistics Definition The average is a measure of central tendency, calculated by dividing the sum of values by their count. Description In statistics, the average is crucial for analyzing data sets, revealing trends, and providing insight into overall performance. It’s applicable in various fields, from school grades to business metrics. For example, if a student scores 80, 90, and 100 on three exams, the average can be calculated as follows: Average = (80 + 90 + 100) / 3 = 90. The average is essential in math education as it forms a foundational concept for more advanced statistical analyses.	Data Analysis
Definition--Measures of Central Tendency--Average Speed	Average Speed Topic Statistics Definition Average speed is the total distance traveled divided by the total time taken. Description This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.	Data Analysis
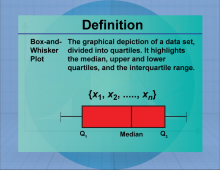
Definition--Measures of Central Tendency--Box-and-Whisker Plot	Box-and-Whisker Plot Topic Statistics Definition A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. Description Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.	Data Analysis
Definition--Measures of Central Tendency--Categorical Data	Categorical Data Topic Statistics Definition Categorical data refers to data that can be divided into specific categories or groups. Description Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.	Data Analysis
Definition--Measures of Central Tendency--Continuous Data	Continuous Data Topic Statistics Definition Continuous data is numerical data that can take any value within a range. Description Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.	Data Analysis
Definition--Measures of Central Tendency--Discrete Data	Discrete Data Topic Statistics Definition Discrete data consists of countable values, often represented by whole numbers. Description Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.	Data Analysis
Definition--Measures of Central Tendency--Geometric Mean	Geometric Mean Topic Statistics Definition The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. Description The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.	Data Analysis
Definition--Measures of Central Tendency--Histogram	Histogram Topic Statistics Definition A histogram is a graphical representation of data distribution using bars of different heights. Description Histograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference.	Data Analysis
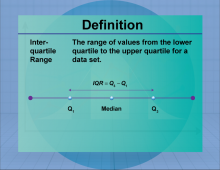
Definition--Measures of Central Tendency--Interquartile Range	Interquartile Range Topic Statistics Definition The interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. Description The IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability.	Data Analysis
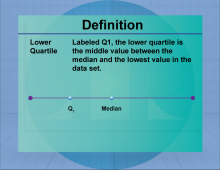
Definition--Measures of Central Tendency--Lower Quartile	Lower Quartile Topic Statistics Definition The lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. Description The lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Mean	Mean Topic Statistics Definition The mean is a measure of central tendency that provides an average representation of a set of data. Description The Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5.	Data Analysis
Definition--Measures of Central Tendency--Median	Median Topic Statistics Definition The median is a measure of central tendency that provides the middle value of a data set.. Description The Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean.	Data Analysis
Definition--Measures of Central Tendency--Median of an Even Data Set	Median of an Even Data Set Topic Statistics Definition The median of an even data set is the mean of two of the terms. Description The Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms.	Data Analysis
Definition--Measures of Central Tendency--Median of an Odd Data Set	Median of an Odd Data Set Topic Statistics Definition The median of an odd data set is one of the terms in the data set. Description The Median is the middle term of a data set. If the data set consists of an odd number of terms, no matter how many terms there are, the Median will be the middle term of that set. In mathematics education, understanding median of an odd data set is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Mode	Mode Topic Statistics Definition The mode is the most frequent data item.. Description The Mode is an important concept in statistics, used to summarize data effectively. It is the most frequent data item in a data set. A data set can have more than one mode. In mathematics education, understanding mode is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Mode of Categorical Data	Mode of Categorical Data Topic Statistics Definition The mode of categorical data is the most frequent item in a categorical data set. Description The Mode of Categorical Data is useful for finding the most frequent data item used with non-numerical data. For example, preferences for discrete characteristics can result in a mode.	Data Analysis
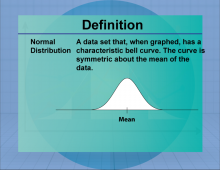
Definition--Measures of Central Tendency--Normal Distribution	Normal Distribution Topic Statistics Definition The normal distribution is a measure of central tendency that provides an average representation of a set of data. Description The Normal Distribution is an important concept in statistics, used to summarize data effectively. In real-world applications, the Normal Distribution helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research.	Data Analysis
Definition--Measures of Central Tendency--Outlier	Outlier Topic Statistics Definition The outlier is is an extreme value for a data set. Description The Outlier is an important concept in statistics. While it doesn't represent the average data set, it does set the range of extreme values in the data set. An outlier can be extremely large or small. In mathematics education, understanding outlier is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.	Data Analysis
Definition--Measures of Central Tendency--Population Mean	Population Mean Topic Statistics Definition The population mean is a measure of central tendency that provides an average representation of a set of data. Description The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.	Data Analysis
Definition--Measures of Central Tendency--Probability Distribution	Probability Distribution Topic Statistics Definition A probability distribution describes how the values of a random variable are distributed. Description Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.	Data Analysis
Definition--Measures of Central Tendency--Quartile	Quartile Topic Statistics Definition Quartiles divide a ranked data set into four equal parts. Description Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.	Data Analysis
Definition--Measures of Central Tendency--Range	Range Topic Statistics Definition The range is the difference between the highest and lowest values in a data set. Description The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.	Data Analysis
Definition--Measures of Central Tendency--Sample Mean	Sample Mean Topic Statistics Definition The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. Description The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.	Data Analysis
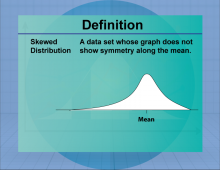
Definition--Measures of Central Tendency--Skewed Distribution	Skewed Distribution Topic Statistics Definition A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side. Description Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.	Data Analysis
Definition--Measures of Central Tendency--Standard Deviation	Standard Deviation Topic Statistics Definition Standard deviation is a measure of the amount of variation or dispersion in a set of values. Description Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.	Data Analysis
Definition--Measures of Central Tendency--Symmetric Distribution	Symmetric Distribution Topic Statistics Definition A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other. Description Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.	Data Analysis
Definition--Measures of Central Tendency--Upper Quartile	Upper Quartile Topic Statistics Definition The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. Description The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.	Data Analysis
Definition--Measures of Central Tendency--Variance	Variance Topic Statistics Definition Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. Description Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.	Data Analysis
Definition--Measures of Central Tendency--Weighted Average	Weighted Average Topic Statistics Definition A weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. Description The weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Measures of Central Tendency--Weighted Mean	Weighted Mean Topic Statistics Definition The weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. Description The weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value.	Data Analysis
Definition--Sequences and Series Concepts--Arithmetic Sequence	Arithmetic Sequence Topic Sequences and Series Definition An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. Description An arithmetic sequence is a fundamental concept in mathematics, particularly in the study of sequences and series. It is defined by the property that each term after the first is the sum of the previous term and a constant, known as the common difference. This concept is crucial in various mathematical applications, including solving problems related to linear growth and predicting future events based on past data.	Sequences
Definition--Sequences and Series Concepts--Arithmetic Series	Arithmetic Series Topic Sequences and Series Definition An arithmetic series is the sum of the terms of an arithmetic sequence. Description An arithmetic series is a significant concept in mathematics, especially in the study of sequences and series. It is formed by adding the terms of an arithmetic sequence. This concept is crucial for understanding how sums of linear patterns are calculated, which has applications in various fields such as finance, engineering, and computer science.	Series
Definition--Sequences and Series Concepts--Binomial Series	Binomial Series Topic Sequences and Series Definition The binomial series is the expansion of a binomial raised to any integer power. Description The binomial series is a powerful tool in mathematics, particularly in the study of sequences and series. It represents the expansion of a binomial expression raised to any integer power, which is essential in various mathematical and scientific applications, including probability, algebra, and calculus.	Series