
Illustrative Math Alignment: Grade 6 Unit 1
Reasoning to Find Area
Lesson 11: Polygons
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Closed Captioned Video: Geometry Applications: Polygons, 1 |
Closed Captioned Video: Geometry Applications: Polygons, 1TopicPolygons DescriptionThis segment introduces polygons through the Pentagon's design. The building’s advantages include increased perimeter and accessibility due to its five-sided structure, illustrating how polygons solve real-world design challenges. Key concepts include perimeter, angles, and design versatility. |
Definition of a Polygon and Applications of Polygons |

|
Closed Captioned Video: Geometry Applications: Polygons, 2 |
Closed Captioned Video: Geometry Applications: Polygons, 2TopicPolygons DescriptionThe segment explores Islamic art’s reliance on geometric patterns formed by regular polygons. It demonstrates how artisans used compasses and straightedges to create precise designs, highlighting properties like congruent sides and angles, and applications in tiling and architecture. |
Definition of a Polygon and Applications of Polygons |

|
Closed Captioned Video: Geometry Applications: Polygons, 3 |
Closed Captioned Video: Geometry Applications: Polygons, 3TopicPolygons DescriptionComposite figures in architecture, like the Petronas Towers, combine polygons to form complex shapes. This segment examines patterns like overlapping squares and calculates areas using properties of triangles and hexagons. Applications include architectural symmetry and efficiency. |
Definition of a Polygon and Applications of Polygons |

|
Definition--Geometry Basics--Hexagon |
HexagonTopicGeometry Basics DefinitionA six-sided polygon. |
Definition of a Polygon |

|
Definition--Geometry Basics--Pentagon |
PentagonTopicGeometry Basics DefinitionA five-sided polygon. DescriptionA pentagon is a polygon with five sides and five angles. This shape is commonly found in both natural and human-made structures. The sum of the interior angles of a pentagon is 540 degrees, calculated using the formula (n − 2) × 180 where n is the number of sides. Understanding pentagons is essential for studying polygon properties and solving geometric problems. |
Definition of a Polygon |

|
Definition--Geometry Basics--Polygon |
PolygonTopicGeometry Basics DefinitionA polygon is a closed two-dimensional shape made up of three or more straight sides. DescriptionPolygons play a central role in geometry. They can be classified into regular and irregular based on side lengths and angles. The sum of the interior angles can be calculated using the formula (n − 2) × 180 where n is the number of sides. For example, a hexagon has six sides and an interior angle sum of 720 degrees. Understanding polygons is crucial for solving complex geometric problems and applying them in real life, including architectural design and animation. |
Definition of a Polygon |

|
Definition--Geometry Basics--Regular Polygon |
Regular PolygonTopicPolygons DefinitionA regular polygon is a closed, two-dimensional shape with all sides equal in length and all interior angles equal in measure. DescriptionRegular polygons are fundamental shapes in geometry, representing perfect symmetry and uniformity. These polygons have several key properties that make them significant in both mathematical theory and practical applications. All vertices of a regular polygon lie on a common circle, known as the circumscribed circle, and there is also an inscribed circle tangent to every side at its midpoint. |
Definition of a Polygon |
|
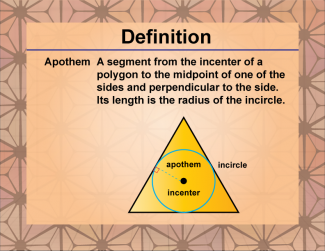
Definition--Polygon Concepts--Apothem |
Polygon Concepts: ApothemTopicPolygons DefinitionThe apothem of a regular polygon is the perpendicular distance from the center of the polygon to the midpoint of one of its sides. DescriptionIn geometry, the apothem is a crucial element for understanding regular polygons, which are polygons with all sides and angles equal. The apothem serves as a key component in various geometric calculations, particularly in determining the area of regular polygons. The formula for the area of a regular polygon is given by: $$A = \frac{1}{2} \cdot a \cdot P$$ |
Definition of a Polygon |

|
Definition--Polygon Concepts--Area of a Polygon |
Area of a PolygonTopicGeometry - Polygon Concepts DefinitionThe area of a polygon is the number of square units contained within its boundaries. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Circumscribed Circle |
Circumscribed CircleDefinitionA circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter, and its radius is called the circumradius. |
Definition of a Polygon |
|
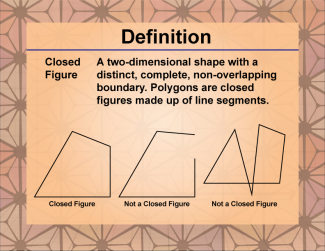
Definition--Polygon Concepts--Closed Figure |
Closed FigureTopicPolygons DefinitionA closed figure is a geometric shape that starts and ends at the same point, forming a complete boundary with no openings. |
Definition of a Polygon |
|
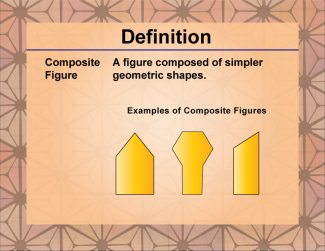
Definition--Polygon Concepts--Composite Figure |
Compound FigureTopicPolygons DefinitionA compound figure is a geometric shape that is composed of two or more simple polygons combined to form a more complex figure. DescriptionIn geometry, a compound figure is a shape that is formed by combining two or more polygons. These figures are significant because they allow for the exploration of more complex shapes and their properties, which can be broken down into simpler, more manageable components. Understanding compound figures is essential for solving problems related to area, perimeter, and other geometric properties. |
Definition of a Polygon |
|
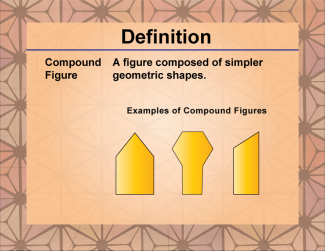
Definition--Polygon Concepts--Compound Figure |
Compound FigureTopicPolygons DefinitionA polygon is a closed two-dimensional shape with straight line segments, while a compound figure is a shape formed by combining two or more geometric figures. |
Definition of a Polygon |
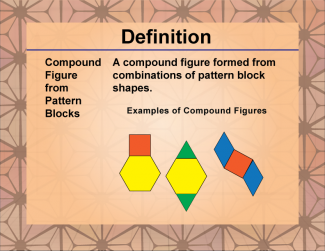
|
Definition--Polygon Concepts--Compound Figure from Pattern Blocks |
Compound Figure from Pattern BlocksTopicPolygons DefinitionA compound figure, also known as a composite figure, is a shape that is made up of two or more simple geometric figures such as triangles, rectangles, squares, parallelograms, trapezoids, and circles. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Concave Polygon |
Concave PolygonTopicPolygons DefinitionA concave polygon is a type of polygon where at least one interior angle is greater than 180 degrees. |
Definition of a Polygon |
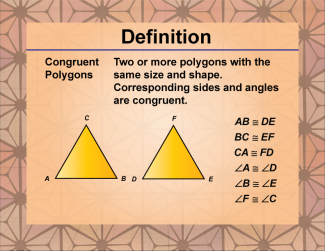
|
Definition--Polygon Concepts--Congruent Polygons |
Congruent PolygonsTopicPolygon Concepts DefinitionCongruent polygons are polygons that have the same shape and size, with corresponding sides and angles being equal. |
Definition of a Polygon |
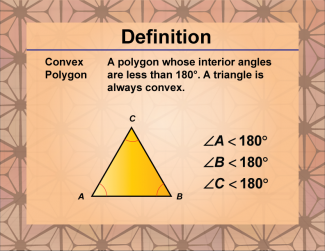
|
Definition--Polygon Concepts--Convex Polygon |
Convex PolygonTopicPolygons DefinitionA convex polygon is a polygon in which all interior angles are less than 180 degrees, and no vertices point inward. |
Definition of a Polygon |
|
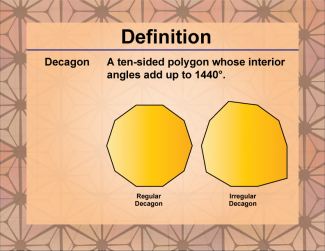
Definition--Polygon Concepts--Decagon |
DecagonTopicPolygons DefinitionA decagon is a ten-sided polygon with ten vertices and ten interior angles. The sum of the interior angles of a decagon is 1440°. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Diagonals of a Polygon |
Diagonals of a PolygonTopicPolygons DefinitionA diagonal of a polygon is a line segment connecting two non-adjacent vertices. |
Definition of a Polygon |
|
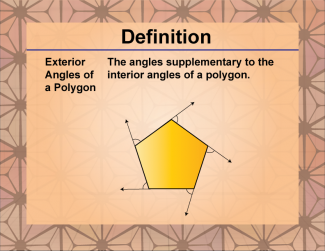
Definition--Polygon Concepts--Exterior Angles of a Polygon |
Exterior Angles of a PolygonTopicPolygons DefinitionAn exterior angle of a polygon is the angle formed between any side of the polygon and the extension of an adjacent side. |
Definition of a Polygon |
|
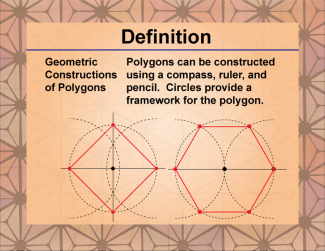
Definition--Polygon Concepts--Geometric Constructions of Polygons |
Geometric Construction of a PolygonTopicPolygon Concepts DefinitionA polygon is a closed two-dimensional figure composed of straight line segments connected end to end. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Hexagon |
HexagonTopicPolygons DefinitionA hexagon is a six-sided polygon with six vertices and six interior angles. DescriptionHexagons play a significant role in geometry and are frequently observed in nature and human-made structures. As a regular polygon, the hexagon possesses unique properties that make it both mathematically interesting and practically useful. Each interior angle of a regular hexagon measures 120°, and the sum of all interior angles is 720°. This shape is notable for its efficiency in space-filling, which is why it's commonly found in structures like honeycombs. |
Definition of a Polygon |
|
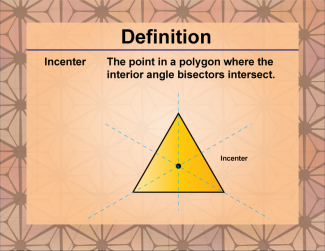
Definition--Polygon Concepts--Incenter |
Incenter of a TriangleTopicPolygons DefinitionThe incenter of a triangle is the point where the angle bisectors of the triangle intersect. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Incircle |
IncircleTopicPolygon Concepts DefinitionAn incircle is the largest circle that can be inscribed within a polygon, tangent to all of its sides. |
Definition of a Polygon |
|
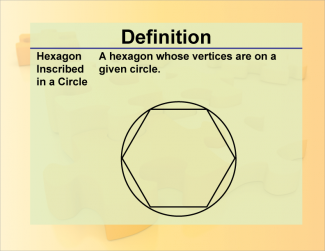
Definition--Polygon Concepts--Inscribed Hexagon |
Inscribed HexagonTopicPolygons and Circle Geometry DefinitionAn inscribed hexagon is a six-sided polygon whose vertices all lie on the circumference of a circle. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Interior Angles of a Polygon |
Sum of Interior Angles of a PolygonTopicPolygons DefinitionThe sum of interior angles of a polygon with n sides is given by the formula: (n - 2) × 180°, where n is the number of sides in the polygon. DescriptionThe sum of interior angles is a fundamental property of polygons that plays a crucial role in geometry. This concept is essential for understanding the structure and properties of various polygons, from simple triangles to complex multi-sided figures. The formula (n - 2) × 180° provides a quick and efficient way to calculate the total measure of all interior angles in any polygon, regardless of its regularity. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Irregular Polygon |
Irregular PolygonTopicPolygons DefinitionAn irregular polygon is a polygon that does not have all sides equal and all angles equal. DescriptionIn geometry, polygons are fundamental shapes that are defined by having three or more straight sides. While regular polygons have sides and angles that are all equal, irregular polygons do not conform to this uniformity. This means that in an irregular polygon, the lengths of the sides can vary, and the measures of the angles can differ from one another. |
Definition of a Polygon |

|
Definition--Polygon Concepts--n-gon |
Definition: Polygon Concepts - n-GonTopicPolygons DefinitionAn n-gon is a polygon with n sides, where n represents any integer greater than or equal to three. DescriptionPolygons are fundamental shapes in geometry, characterized by their straight sides and closed forms. The term n-gon is a general way to refer to polygons with n sides, where n can be any integer starting from three. Common examples include triangles (3-gon), quadrilaterals (4-gon), pentagons (5-gon), and so on. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Octagon |
OctagonTopicPolygons DefinitionAn octagon is a polygon with eight sides and eight angles. DescriptionIn geometry, an octagon is a significant shape due to its unique properties and applications. An octagon has eight sides of equal or varying lengths, and the sum of its interior angles is always 1080 degrees. This makes it a versatile shape in both theoretical and practical applications. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Pentagon |
Definition--Polygon Concepts--PentagonTopicPolygons DefinitionA pentagon is a polygon with five sides and five angles. DescriptionThe pentagon is a fundamental shape in geometry, belonging to the family of polygons. As a five-sided figure, it plays a significant role in both theoretical mathematics and practical applications. Pentagons can be regular, where all sides and angles are equal, or irregular, with varying side lengths and angle measures. In a regular pentagon, each interior angle measures 108 degrees, contributing to a total of 540 degrees for all interior angles. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Perimeter of a Polygon |
Polygon PerimeterTopicPolygons DefinitionThe perimeter of a polygon is the total length of its sides. DescriptionThe concept of the perimeter is fundamental in geometry, particularly when dealing with polygons. A polygon is a closed figure with straight sides, and its perimeter is the sum of the lengths of all these sides. Understanding the perimeter is crucial for various practical applications such as determining the boundary length of a plot of land, the amount of material needed to fence a garden, or the trim required to frame a picture. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Polygon |
PolygonDefinitionA polygon is a closed figure on a plane with straight sides and vertices. Examples of polygons include triangles, quadrilaterals, pentagons, and hexagons. DescriptionIn geometry, polygons are fundamental shapes that form the basis for more complex structures and concepts. They are defined as closed plane figures with straight sides. Each side intersects exactly two other sides at its endpoints, creating vertices. Polygons are classified based on the number of sides they have: triangles (3 sides), quadrilaterals (4 sides), pentagons (5 sides), and so on. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Polygon Coordinates |
Polygon CoordinatesTopicGeometry: Polygons DefinitionPolygon coordinates are the ordered pairs (x, y) that represent the vertices of a polygon in a coordinate plane. DescriptionPolygon coordinates play a crucial role in analytical geometry and are fundamental to understanding and working with polygons in a coordinate system. These coordinates allow us to precisely define the shape, size, and position of a polygon on a two-dimensional plane. By using ordered pairs (x, y), we can pinpoint each vertex of the polygon, enabling various calculations and analyses. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Polygon Symmetry |
Polygon SymmetryTopicPolygons DefinitionPolygon symmetry refers to the property of a polygon being invariant under certain transformations, such as reflections or rotations. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Polygon Vertices |
Definition--Polygon Concepts--Polygon VerticesTopicPolygons DefinitionA vertex (plural: vertices) of a polygon is a point where two sides of the polygon meet. DescriptionIn geometry, understanding the concept of vertices is fundamental to the study of polygons. A vertex is essentially a corner point where two sides of a polygon intersect. For instance, a triangle has three vertices, a quadrilateral has four, and a pentagon has five. The vertices are crucial in defining the shape and structure of a polygon, as they determine the angles and the overall geometry of the figure. |
Definition of a Polygon |
|
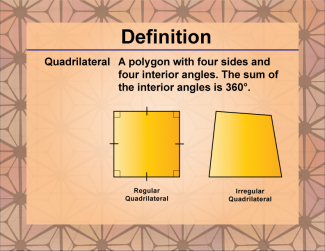
Definition--Polygon Concepts--Quadrilateral |
Definition--Polygon Concepts--QuadrilateralTopicPolygons DefinitionA quadrilateral is a polygon with four sides, four vertices, and four angles. The sum of the interior angles of a quadrilateral is always 360 degrees. DescriptionQuadrilaterals are fundamental shapes in geometry, characterized by their four sides and four vertices. They serve as a bridge between simpler shapes like triangles and more complex polygons, making them essential for understanding geometric principles and properties. The study of quadrilaterals involves exploring various types such as squares, rectangles, trapezoids, and parallelograms, each with unique properties and applications. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Regular Polygon |
Regular PolygonsTopicPolygons DefinitionA regular polygon is a polygon with all sides and angles equal. DescriptionRegular polygons play a significant role in geometry due to their symmetrical properties and uniformity. These shapes are defined by having all sides of equal length and all interior angles of equal measure. This symmetry makes regular polygons a fundamental subject of study in various fields of mathematics and applied sciences. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Similar Polygons |
Similar PolygonsTopicPolygons DefinitionSimilar polygons are polygons that have the same shape but may differ in size. Their corresponding angles are equal, and their corresponding sides are proportional. DescriptionIn geometry, the concept of similar polygons is fundamental. Similar polygons maintain the same shape but can vary in size. This means that all corresponding angles between the two polygons are equal, and the lengths of corresponding sides are proportional. For instance, two triangles are similar if their corresponding angles are equal and the lengths of their corresponding sides are in the same ratio. |
Definition of a Polygon |
|
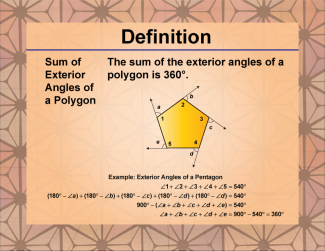
Definition--Polygon Concepts--Sum of the Exterior Angles of a Polygon |
Sum of Exterior Angles of a PolygonTopicPolygons DefinitionThe sum of the exterior angles of any polygon, regardless of the number of sides, is always 360°. DescriptionThe sum of exterior angles of a polygon is a fundamental concept in geometry that holds true for all polygons, regardless of their shape or number of sides. This property is crucial for understanding the nature of polygons and their relationship to circular motion. Exterior angles are formed by extending each side of the polygon and measuring the angle between this extension and the adjacent side. |
Definition of a Polygon |
|
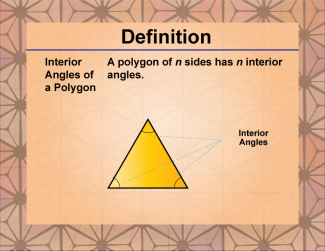
Definition--Polygon Concepts--Sum of the Interior Angles of a Polygon |
Interior Angles of a PolygonTopicPolygons DefinitionAn interior angle of a polygon is an angle formed inside the polygon by two adjacent sides. |
Definition of a Polygon |
|
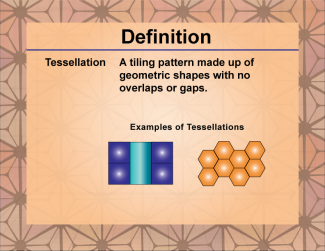
Definition--Polygon Concepts--Tessellation |
TessellationTopicPolygons DefinitionA tessellation is a repeating pattern of geometric shapes that covers a plane without gaps or overlaps. DescriptionTessellations are fascinating geometric arrangements that play a significant role in both mathematics and art. They occur when a surface is completely covered by repeating shapes, leaving no gaps or overlaps. In geometry, tessellations demonstrate how certain shapes can fit together perfectly to create intricate patterns. The most common shapes used in tessellations are regular polygons, such as triangles, squares, and hexagons, due to their uniform angles and sides. |
Definition of a Polygon |
|
Definition--Polygon Concepts--Triangle |
TriangleTopicPolygons DefinitionA triangle is a polygon with three sides and three angles. DescriptionTriangles are fundamental shapes in geometry, serving as the building blocks for many complex geometric figures and concepts. Their simplicity and versatility make them crucial in various mathematical and real-world applications. Triangles are classified based on their side lengths and angle measures, leading to categories such as equilateral, isosceles, and scalene triangles, as well as right, acute, and obtuse triangles. |
Definition of a Polygon |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Interior Angles of a Polygon |
In this Slide Show, apply concepts of linear functions to the context of the interior angles of a polygon. Note: The download is a PPT file. |
Definition of a Polygon |

|
INSTRUCTIONAL RESOURCE: Math Examples 37 |
INSTRUCTIONAL RESOURCE: Math Examples--Polygon Classification
This set of tutorials provides 36 examples of how to classify polygons based on side and angle characteristics. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Definition of a Polygon |

|
Interactive Math Game--Memory Game: Polygons |
Interactive Math Game--Memory Game: Polygons
Use this math game to review polygons. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Polygon |

|
Math Clip Art--Geometry Basics--Polygon Basics 01 |
Math Clip Art--Geometry Basics--Polygon Basics 01TopicGeometry Basics DescriptionThis image is part of a series designed to teach fundamental concepts about polygons. It serves as a title card, prominently displaying the words "Polygon Basics" to introduce students to the topic. The use of clear, bold text on a simple background helps focus attention and set the stage for the lessons to follow. |
Definition of a Polygon |

|
Math Clip Art--Geometry Basics--Polygon Basics 02 |
Math Clip Art--Geometry Basics--Polygon Basics 02TopicGeometry Basics DescriptionThis image is part of a series designed to teach fundamental concepts about polygons. It presents a table that correlates the number of sides with the names of different polygons. The caption emphasizes that the number of sides determines the type of polygon, providing a clear, visual representation of this important concept. |
Definition of a Polygon |

|
Math Clip Art--Geometry Basics--Polygon Basics 03 |
Math Clip Art--Geometry Basics--Polygon Basics 03TopicGeometry Basics DescriptionThis image is part of a series designed to teach fundamental concepts about polygons. It features an illustration of a regular pentagon, accompanied by a caption explaining that a regular polygon has congruent sides and congruent angles. This visual representation helps students understand the defining characteristics of regular polygons. |
Definition of a Polygon |

|
Math Clip Art--Geometry Basics--Polygon Basics 04 |
Math Clip Art--Geometry Basics--Polygon Basics 04TopicGeometry Basics DescriptionThis image is part of a series designed to teach fundamental concepts about polygons. It presents a side-by-side comparison of an irregular triangle and a regular triangle, with a caption stating that polygons can be either regular or irregular. This visual juxtaposition effectively illustrates the difference between these two types of polygons. |
Definition of a Polygon |

|
Math Clip Art--Geometry Basics--Polygon Basics 05 |
Math Clip Art--Geometry Basics--Polygon Basics 05TopicGeometry Basics DescriptionThis image is part of a series designed to teach fundamental concepts about polygons. It showcases an irregular quadrilateral alongside a regular quadrilateral, reinforcing the concept that polygons can be either regular or irregular. This visual comparison helps students understand the distinction between these two categories of quadrilaterals. |
Definition of a Polygon |