
Illustrative Math Alignment: Grade 6 Unit 8
Data Sets and Distributions
Lesson 18: Using Data to Solve Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
SAT Math Lesson Plan 11: Data Interpretation | SAT Math Lesson Plan 11: Data Interpretation Lesson 11 of this SAT Math Prep series focuses on data interpretation—a key skill area tested on the SAT that accounts for approximately 15–20% of the math section. In this 45-minute lesson, students will explore how to analyze and interpret data presented in various formats including tables, bar graphs, line graphs, scatterplots, histograms, circle graphs, and box-and-whisker plots. Students will practice calculating statistical measures such as mean and median, identifying outliers, and recognizing trends and correlations in real-world contexts. The lesson includes a step-by-step Warm-Up, seven detailed examples with visuals, a Review section with guided practice, and a 10-question multiple-choice quiz modeled after actual SAT items. Downloadable images of each graph are included for easy classroom projection or digital use. |
Data Analysis |

|
Math in the News: Issue 117--Box Office Hits and Misses | Math in the News: Issue 117 | Box Office Hits and Misses
December 2022. In this issue of Math in the News we look at box office hits and misses from Disney. The House of Blockbosters every now and then misfires. It's useful to analyze box office data to see what we can learn from the hits and misses. —PRESS PREVIEW TO SEE THE SLIDE SHOW— This is part of the Math in the News collection. To see the complete collection, click on this link.Note: The download is a PPT file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |
|
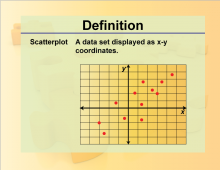
Definition--Charts and Graphs--Scatterplot | Definition--Charts and Graphs--Scatterplot
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Stem-and-Leaf Plot | Definition--Charts and Graphs--Stem-and-Leaf Plot
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Pictograph | Definition--Charts and Graphs--Pictograph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Scaled Pictograph | Definition--Charts and Graphs--Scaled Pictograph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
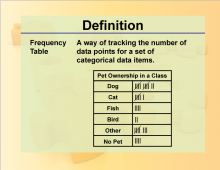
Definition--Charts and Graphs--Frequency Table | Definition--Charts and Graphs--Frequency Table
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
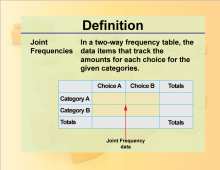
Definition--Charts and Graphs--Joint Frequencies | Definition--Charts and Graphs--Joint Frequencies
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Two-Way Frequency Table | Definition--Charts and Graphs--Two-Way Frequency Table
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
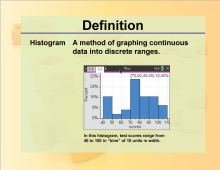
Definition--Charts and Graphs--Histogram | Definition--Charts and Graphs--Histogram
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
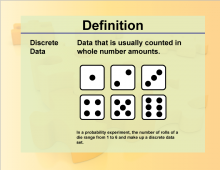
|
Definition--Charts and Graphs--Discrete Data | Definition--Charts and Graphs--Discrete Data
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Continuous Data | Definition--Charts and Graphs--Continuous Data
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Categorical Data | Definition--Charts and Graphs--Categorical Data
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Instructional Resource: Quadratic Regression on Desmos | INSTRUCTIONAL RESOURCE: Tutorial: Quadratic Regression on Desmos
In this tutorial we walk students through the steps of doing a quadratic regression on a Desmos graphing calculator. The steps include showing how to create pseudo-quadratic data on a spreadsheet. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Quadratic Equations and Functions and Data Analysis |

|
Arithmetic Application: Counting Bison | In this application of arithmetic, students analyze the changing population of bison in the Americas. Using real-world data and applying key math concepts, students will do some sophisticated analysis using basic skills. These are the key math concepts covered: Place value Skip counting Doubling Data analysis Given the wide disparity in the population of bison over several centuries, students will be analyzing data in the millions but using place value to gain a clear understanding of the numbers involved. Skip counting will be used to analyze changes to populations, including patterns than involve doubling. Students will be actively engaged with the subject matter and will develop a mathematical mindset around data. This is an excellent preparation for the data analysis developed in upper elementary and middle school. |
Addition Expressions and Equations, Complete Number Patterns, Counting and Place Value |

|
Math in the News: Issue 116: The 2021 Olympics | Math in the News: Issue 116: The 2021 Olympics
August 2021. In this issue of Math in the News we look at various charts and statistics about the Tokyo Olympics. Students are shown a series of charts and are then asked questions to encourage them to analyze the data. This is an excellent back-to-school activity with the focus on real-world data. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Definition--Sequences and Series Concepts--Sequences | SequencesTopicSequences and Series DefinitionA sequence is an ordered list of numbers that follow a particular pattern or rule. DescriptionSequences are fundamental concepts in mathematics, representing ordered lists of numbers that follow a specific pattern or rule. This concept is crucial in various mathematical applications, including algebra, calculus, and computer science. |
Sequences |

|
Definition--Sequences and Series Concepts--Finite Sequence | Finite SequenceTopicSequences and Series DefinitionA finite sequence is a sequence that has a limited number of terms. DescriptionA finite sequence is a sequence with a specific number of terms, making it a crucial concept in the study of sequences and series. This concept is fundamental in various mathematical applications where the number of elements is limited, such as in statistics and computer science. In real-world applications, finite sequences are used in data analysis, where datasets have a specific number of entries. They are also used in computer algorithms that process a fixed number of elements. Algebraically, a finite sequence can be represented as |
Sequences |

|
Definition--Sequences and Series Concepts--Infinite Sequence | Infinite SequenceTopicSequences and Series DefinitionAn infinite sequence is a sequence that continues indefinitely without terminating. DescriptionAn infinite sequence is a fundamental concept in mathematics, representing a sequence that continues indefinitely without terminating. This concept is essential in various mathematical and scientific applications, including calculus and analysis. In real-world applications, infinite sequences are used in mathematical modeling and simulations where processes continue indefinitely, such as in population dynamics or financial forecasting. Algebraically, an infinite sequence can be represented as |
Sequences |

|
Definition--Sequences and Series Concepts--Series | SeriesTopicSequences and Series DefinitionA series is the sum of the terms of a sequence. DescriptionSeries are significant concepts in mathematics, representing the sum of the terms of a sequence. This concept is essential in various mathematical and scientific applications, including calculus, analysis, and financial modeling. In real-world applications, series are used in financial calculations, such as determining the total amount of payments or investments over time. They are also used in data analysis to find the sum of a dataset. Algebraically, series can be represented in various forms, such as arithmetic series, geometric series, and more. |
Series |

|
Definition--Sequences and Series Concepts--Finite Series | Finite SeriesTopicSequences and Series DefinitionA finite series is the sum of the terms of a finite sequence. DescriptionA finite series is a significant concept in mathematics, representing the sum of the terms of a finite sequence. This concept is essential in various mathematical and scientific applications, including statistics, finance, and computer science. In real-world applications, finite series are used in financial calculations, such as determining the total amount of payments over a fixed period. They are also used in data analysis to find the sum of a dataset. Algebraically, a finite series can be expressed as |
Series |

|
Definition--Sequences and Series Concepts--Infinite Series | Infinite SeriesTopicSequences and Series DefinitionAn infinite series is the sum of the terms of an infinite sequence. DescriptionAn infinite series is a significant concept in mathematics, representing the sum of the terms of an infinite sequence. This concept is essential in various mathematical and scientific applications, including calculus and analysis. In real-world applications, infinite series are used in mathematical modeling and simulations where processes continue indefinitely, such as in signal processing or financial forecasting. Algebraically, an infinite series can be represented as |
Series |

|
Definition--Sequences and Series Concepts--Convergent Series | Convergent SeriesTopicSequences and Series DefinitionA convergent series is a series whose terms approach a specific value as the number of terms increases. DescriptionA convergent series is a critical concept in the study of sequences and series, where the sum of its terms approaches a finite limit as the number of terms increases. This concept is essential in various mathematical and scientific applications, including calculus and analysis. |
Series |

|
Definition--Sequences and Series Concepts--Divergent Series | Divergent SeriesTopicSequences and Series DefinitionA divergent series is a series whose terms do not approach a specific value as the number of terms increases. DescriptionA divergent series is a significant concept in the study of sequences and series, where the sum of its terms does not approach a finite limit as the number of terms increases. This concept is essential in various mathematical and scientific applications, including calculus and analysis. |
Series |

|
Definition--Sequences and Series Concepts--Binomial Series | Binomial SeriesTopicSequences and Series DefinitionThe binomial series is the expansion of a binomial raised to any integer power. DescriptionThe binomial series is a powerful tool in mathematics, particularly in the study of sequences and series. It represents the expansion of a binomial expression raised to any integer power, which is essential in various mathematical and scientific applications, including probability, algebra, and calculus. |
Series |

|
Definition--Sequences and Series Concepts--Binomial Theorem | Binomial TheoremTopicSequences and Series DefinitionThe binomial theorem describes the algebraic expansion of powers of a binomial. DescriptionThe binomial theorem is a fundamental theorem in algebra that provides a formula for expanding binomials raised to any positive integer power. This theorem is essential in various mathematical disciplines, including algebra, calculus, and probability theory. |
Series |

|
Definition--Sequences and Series Concepts--Pascal's Triangle | Pascal's TriangleTopicSequences and Series DefinitionPascal's Triangle is a triangular array of binomial coefficients. DescriptionPascal's Triangle is a fundamental concept in mathematics, representing a triangular array of binomial coefficients. This concept is essential in various mathematical and scientific applications, including combinatorics, algebra, and probability theory. In real-world applications, Pascal's Triangle is used in probability calculations, particularly in binomial expansions and combinatorial problems. It is also used in computer science for algorithm design. Algebraically, the elements of Pascal's Triangle can be expressed as |
Series |

|
Definition--Sequences and Series Concepts--Recursive Formula | Recursive FormulaTopicSequences and Series DefinitionA recursive formula defines each term of a sequence using the preceding term(s). DescriptionA recursive formula is a fundamental concept in mathematics, representing a way to define each term of a sequence using the preceding term(s). This concept is essential in various mathematical and scientific applications, including computer science and algorithm design. |
Series |

|
Definition--Sequences and Series Concepts--Explicit Formula for a Sequence | Explicit Formula for a SequenceTopicSequences and Series DefinitionAn explicit formula for a sequence provides a direct way to calculate any term in the sequence. DescriptionAn explicit formula for a sequence is a mathematical expression that allows for the direct computation of any term in the sequence without needing to know the previous terms. This concept is fundamental in the study of sequences and series and is widely used in various mathematical applications. |
Sequences |

|
Definition--Sequences and Series Concepts--Common Difference | Common DifferenceTopicSequences and Series DefinitionThe common difference is the difference between consecutive terms in an arithmetic sequence. DescriptionThe common difference is a key concept in arithmetic sequences, representing the consistent interval between consecutive terms. This concept is fundamental in understanding linear patterns and is widely used in various mathematical applications. |
Sequences |

|
Definition--Sequences and Series Concepts--Common Ratio | Common RatioTopicSequences and Series DefinitionThe common ratio is the ratio between consecutive terms in a geometric sequence. DescriptionThe common ratio is a fundamental concept in geometric sequences, representing the consistent factor by which each term is multiplied to obtain the next term. This concept is crucial in understanding exponential growth and decay, which are prevalent in various mathematical and scientific applications. |
Sequences |

|
Definition--Sequences and Series Concepts--Summation Notation | Summation NotationTopicSequences and Series DefinitionSummation notation is a mathematical notation used to represent the sum of a sequence of terms. DescriptionSummation notation is a powerful tool in mathematics, representing the sum of a sequence of terms in a compact form. This concept is essential in various mathematical and scientific applications, including calculus, statistics, and computer science. |
Series |

|
Definition--Sequences and Series Concepts--Fibonacci Sequence | Fibonacci SequenceTopicSequences and Series DefinitionThe Fibonacci sequence is a sequence where each term is the sum of the two preceding ones, starting from 0 and 1. DescriptionThe Fibonacci sequence is a famous sequence in mathematics, where each term is the sum of the two preceding ones, starting from 0 and 1. This sequence is significant in various mathematical and scientific applications, including computer science, biology, and art. |
Sequences |

|
Definition--Sequences and Series Concepts--Triangular Numbers | Triangular NumbersTopicSequences and Series DefinitionTriangular numbers are numbers that can be represented by an equilateral triangle. DescriptionTriangular numbers are fundamental concepts in mathematics, representing numbers that can form an equilateral triangle. This concept is crucial in various mathematical applications, including algebra, geometry, and number theory. In real-world applications, triangular numbers are used in combinatorial problems and in determining the number of connections in a network. They are also used in computer algorithms and game design. Algebraically, triangular numbers can be represented as |
Sequences |

|
Definition--Sequences and Series Concepts--Square Numbers | Square NumbersTopicSequences and Series DefinitionSquare numbers are numbers that are the square of an integer. DescriptionSquare numbers are fundamental concepts in mathematics, representing numbers that are the square of an integer. This concept is crucial in various mathematical applications, including algebra, geometry, and number theory. In real-world applications, square numbers are used in area calculations, particularly in determining the area of squares. They are also used in computer algorithms and cryptography. Algebraically, square numbers can be represented as n2 , where n is an integer. |
Sequences |
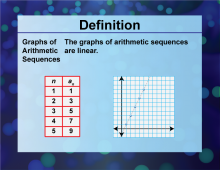
|
Definition--Sequences and Series Concepts--Graphs of Arithmetic Sequences | Graphs of Arithmetic SequencesTopicSequences and Series DefinitionGraphs of arithmetic sequences form a linear graph on a coordinate plane. DescriptionGraphs of arithmetic sequences are a visual tool used in mathematics to represent the terms of an arithmetic sequence on a coordinate plane. This concept is crucial for understanding linear patterns and relationships in sequences and series. |
Sequences |
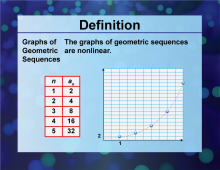
|
Definition--Sequences and Series Concepts--Graphs of Geometric Sequences | Graphs of Geometric SequencesTopicSequences and Series DefinitionGraphs of geometric sequences visually represent the terms of a geometric sequence on a coordinate plane. These are nonlinear graphs. DescriptionGraphs of geometric sequences are a visual tool used in mathematics to represent the terms of a geometric sequence on a coordinate plane. This concept is crucial for understanding exponential patterns and relationships in sequences and series. |
Sequences |

|
Definition--Measures of Central Tendency--Average | AverageTopicStatistics DefinitionThe average is a measure of central tendency, calculated by dividing the sum of values by their count. DescriptionIn statistics, the average is crucial for analyzing data sets, revealing trends, and providing insight into overall performance. It’s applicable in various fields, from school grades to business metrics. For example, if a student scores 80, 90, and 100 on three exams, the average can be calculated as follows: Average = (80 + 90 + 100) / 3 = 90. The average is essential in math education as it forms a foundational concept for more advanced statistical analyses. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Average | Weighted AverageTopicStatistics DefinitionA weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. DescriptionThe weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Average Speed | Average SpeedTopicStatistics DefinitionAverage speed is the total distance traveled divided by the total time taken. DescriptionThis concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations. |
Data Analysis |

|
Definition--Measures of Central Tendency--Sample Mean | Sample MeanTopicStatistics DefinitionThe sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size. DescriptionThe sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations. |
Data Analysis |

|
Definition--Measures of Central Tendency--Population Mean | Population MeanTopicStatistics DefinitionThe population mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon. |
Data Analysis |

|
Definition--Measures of Central Tendency--Geometric Mean | Geometric MeanTopicStatistics DefinitionThe geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth. DescriptionThe geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay. |
Data Analysis |

|
Definition--Measures of Central Tendency--Quartile | QuartileTopicStatistics DefinitionQuartiles divide a ranked data set into four equal parts. DescriptionQuartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends. |
Data Analysis |
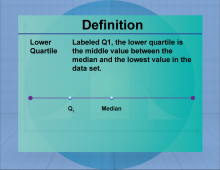
|
Definition--Measures of Central Tendency--Lower Quartile | Lower QuartileTopicStatistics DefinitionThe lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile. DescriptionThe lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Upper Quartile | Upper QuartileTopicStatistics DefinitionThe upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. DescriptionThe upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels. |
Data Analysis |
|
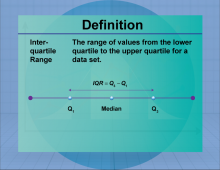
Definition--Measures of Central Tendency--Interquartile Range | Interquartile RangeTopicStatistics DefinitionThe interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set. DescriptionThe IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability. |
Data Analysis |
|
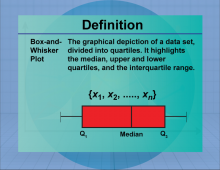
Definition--Measures of Central Tendency--Box-and-Whisker Plot | Box-and-Whisker PlotTopicStatistics DefinitionA box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles. DescriptionBox-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median of an Odd Data Set | Median of an Odd Data SetTopicStatistics DefinitionThe median of an odd data set is one of the terms in the data set. DescriptionThe Median is the middle term of a data set. If the data set consists of an odd number of terms, no matter how many terms there are, the Median will be the middle term of that set. In mathematics education, understanding median of an odd data set is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques. |
Data Analysis |