
Illustrative Math Alignment: Grade 6 Unit 8
Data Sets and Distributions
Lesson 3: Representing Data Graphically
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
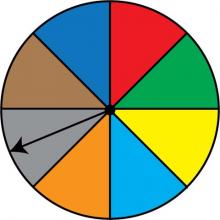
Math Clip Art: Spinner, 8 Sections--Result 6 | Math Clip Art: Spinner, 8 Sections--Result 6TopicProbability and Statistics DescriptionThis image features a spinner divided into eight equal sections colored red, green, yellow, light blue, orange, grey, brown, and dark blue. The spinner's arrow points to the grey section, demonstrating one of the possible outcomes. In the realm of Probability and Statistics, this spinner illustrates how the sample space expands with more outcomes, each having an equal probability of 1/8. It serves as an excellent tool for teaching about equiprobable events in complex scenarios. |
Probability |
|
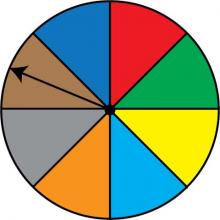
Math Clip Art: Spinner, 8 Sections--Result 7 | Math Clip Art: Spinner, 8 Sections--Result 7TopicProbability and Statistics DescriptionThis image features a spinner divided into eight equal sections colored red, green, yellow, light blue, orange, grey, brown, and dark blue. The spinner's arrow points to the brown section, demonstrating one of the possible outcomes. In the realm of Probability and Statistics, this spinner illustrates how the sample space expands with more outcomes, each having an equal probability of 1/8. It serves as an excellent tool for teaching about equiprobable events in complex scenarios. |
Probability |
|
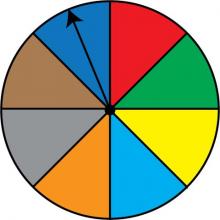
Math Clip Art: Spinner, 8 Sections--Result 8 | Math Clip Art: Spinner, 8 Sections--Result 8TopicProbability and Statistics DescriptionThis image features a spinner divided into eight equal sections colored red, green, yellow, light blue, orange, grey, brown, and dark blue. The spinner's arrow points to the dark blue section, demonstrating one of the possible outcomes. In the realm of Probability and Statistics, this spinner illustrates how the sample space expands with more outcomes, each having an equal probability of 1/8. It serves as an excellent tool for teaching about equiprobable events in complex scenarios. |
Probability |
|
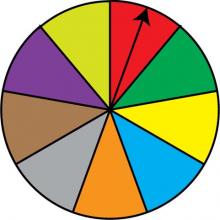
Math Clip Art: Spinner, 9 Sections--Result 1 | Math Clip Art: Spinner, 9 Sections--Result 1TopicProbability and Statistics DescriptionThis image features a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the red section, demonstrating one of the nine possible outcomes. In the realm of Probability and Statistics, this spinner illustrates how the sample space expands with more outcomes, each having an equal probability of 1/9. It serves as an excellent tool for teaching about equiprobable events in complex scenarios. |
Probability |
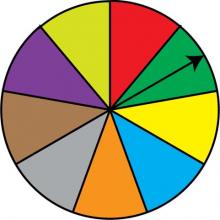
|
Math Clip Art: Spinner, 9 Sections--Result 2 | Math Clip Art: Spinner, 9 Sections--Result 2TopicProbability and Statistics DescriptionThis image showcases a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the green section, illustrating another possible outcome. In Probability and Statistics, this spinner represents a fair probability experiment with nine mutually exclusive and equally likely outcomes. It provides a visual representation of how each spin has an equal 1/9 chance of landing on any of the nine colors. |
Probability |
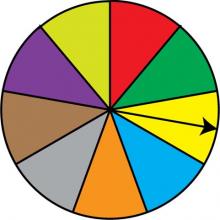
|
Math Clip Art: Spinner, 9 Sections--Result 3 | Math Clip Art: Spinner, 9 Sections--Result 3TopicProbability and Statistics DescriptionThis image displays a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the dark yellow section, showcasing another possible outcome in this probability model. In the field of Probability and Statistics, this spinner exemplifies a uniform probability distribution with nine equally likely outcomes. Each spin has a 1/9 probability of landing on any given color, illustrating the concept of equiprobable events in a more complex scenario. |
Probability |
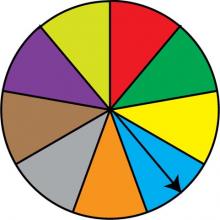
|
Math Clip Art: Spinner, 9 Sections--Result 4 | Math Clip Art: Spinner, 9 Sections--Result 4TopicProbability and Statistics DescriptionThis image presents a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the light blue section, demonstrating another possible outcome in this probability model. In Probability and Statistics, this spinner illustrates a fair probability experiment with nine mutually exclusive and equally likely outcomes. It provides a visual representation of how each spin has an equal 1/9 chance of landing on any of the nine colors. |
Probability |
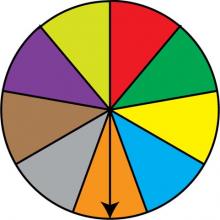
|
Math Clip Art: Spinner, 9 Sections--Result 5 | Math Clip Art: Spinner, 9 Sections--Result 5TopicProbability and Statistics DescriptionThis image showcases a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the orange section, illustrating another possible outcome in this probability model. In the context of Probability and Statistics, this spinner represents a probability experiment with nine equally likely outcomes. It visually demonstrates the concepts of sample space and individual events within that space, each with a 1/9 probability of occurrence. |
Probability |
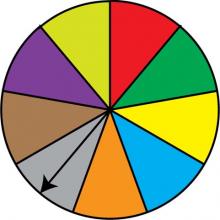
|
Math Clip Art: Spinner, 9 Sections--Result 6 | Math Clip Art: Spinner, 9 Sections--Result 6TopicProbability and Statistics DescriptionThis image displays a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the grey section, showcasing another possible outcome in this probability model. In the field of Probability and Statistics, this spinner exemplifies a uniform probability distribution with nine equally likely outcomes. Each spin has a 1/9 probability of landing on any given color, illustrating the concept of equiprobable events in a more complex scenario. |
Probability |
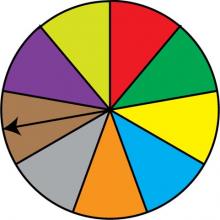
|
Math Clip Art: Spinner, 9 Sections--Result 7 | Math Clip Art: Spinner, 9 Sections--Result 7TopicProbability and Statistics DescriptionThis image presents a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the brown section, demonstrating another possible outcome in this probability model. In Probability and Statistics, this spinner illustrates a fair probability experiment with nine mutually exclusive and equally likely outcomes. It provides a visual representation of how each spin has an equal 1/9 chance of landing on any of the nine colors. |
Probability |
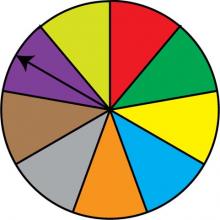
|
Math Clip Art: Spinner, 9 Sections--Result 8 | Math Clip Art: Spinner, 9 Sections--Result 8TopicProbability and Statistics DescriptionThis image showcases a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the purple section, illustrating another possible outcome in this probability model. In the context of Probability and Statistics, this spinner represents a probability experiment with nine equally likely outcomes. It visually demonstrates the concepts of sample space and individual events within that space, each with a 1/9 probability of occurrence. |
Probability |
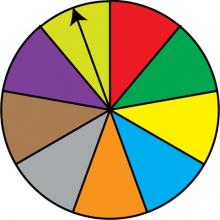
|
Math Clip Art: Spinner, 9 Sections--Result 9 | Math Clip Art: Spinner, 9 Sections--Result 9TopicProbability and Statistics DescriptionThis image displays a spinner divided into nine equal sections colored red, green, dark yellow, light blue, orange, grey, brown, purple, and light yellow. The spinner's arrow points to the light yellow section, showcasing the final possible outcome in this probability model. In the field of Probability and Statistics, this spinner exemplifies a uniform probability distribution with nine equally likely outcomes. Each spin has a 1/9 probability of landing on any given color, illustrating the concept of equiprobable events in a more complex scenario. |
Probability |

|
Definition--Sequences and Series Concepts--Arithmetic Sequence | Arithmetic SequenceTopicSequences and Series DefinitionAn arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. DescriptionAn arithmetic sequence is a fundamental concept in mathematics, particularly in the study of sequences and series. It is defined by the property that each term after the first is the sum of the previous term and a constant, known as the common difference. This concept is crucial in various mathematical applications, including solving problems related to linear growth and predicting future events based on past data. |
Sequences |

|
Definition--Sequences and Series Concepts--Arithmetic Series | Arithmetic SeriesTopicSequences and Series DefinitionAn arithmetic series is the sum of the terms of an arithmetic sequence. DescriptionAn arithmetic series is a significant concept in mathematics, especially in the study of sequences and series. It is formed by adding the terms of an arithmetic sequence. This concept is crucial for understanding how sums of linear patterns are calculated, which has applications in various fields such as finance, engineering, and computer science. |
Series |
|
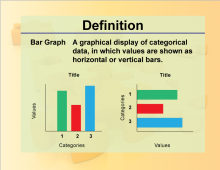
Definition--Charts and Graphs--Bar Graph | Definition--Charts and Graphs--Bar Graph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |
|
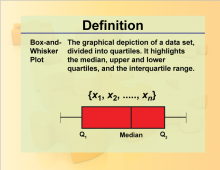
Definition--Charts and Graphs--Box-and-Whisker Plot | Definition--Charts and Graphs--Box-and-Whisker Plot
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Circle Graph | Definition--Charts and Graphs--Circle Graph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Sequences and Series Concepts--Geometric Sequence | Geometric SequenceTopicSequences and Series DefinitionA geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. DescriptionA geometric sequence is a fundamental concept in mathematics, particularly in the study of sequences and series. It is defined by the property that each term after the first is the product of the previous term and a constant, known as the common ratio. This concept is crucial in various mathematical applications, including exponential growth and decay. |
Sequences |

|
Definition--Sequences and Series Concepts--Geometric Series | Geometric SeriesTopicSequences and Series DefinitionA geometric series is the sum of the terms of a geometric sequence. DescriptionA geometric series is a significant concept in mathematics, especially in the study of sequences and series. It is formed by adding the terms of a geometric sequence. This concept is crucial for understanding how sums of exponential patterns are calculated, which has applications in various fields such as finance, engineering, and computer science. |
Series |
|
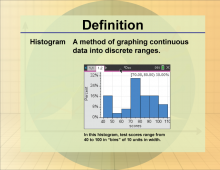
Definition--Statistics and Probability Concepts--Histogram | HistogramTopicStatistics and Probability DefinitionA histogram is a graphical representation of data distribution using bars of different heights. DescriptionHistograms are a fundamental tool in statistics for visualizing the frequency distribution of a dataset. They are used across various fields, including economics, biology, and engineering, to analyze data patterns and trends. By displaying data in intervals, histograms help identify the shape, central tendency, and variability of data. For students, understanding histograms is crucial for interpreting data visually and making informed decisions based on statistical evidence. |
Data Analysis |
|
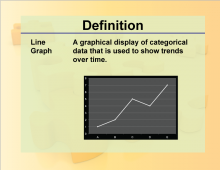
Definition--Charts and Graphs--Line Graph | Definition--Charts and Graphs--Line Graph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Line Plot | Definition--Charts and Graphs--Line Plot
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mode | ModeTopicStatistics DefinitionThe mode is the most frequent data item.. DescriptionThe Mode is an important concept in statistics, used to summarize data effectively. It is the most frequent data item in a data set. A data set can have more than one mode. In mathematics education, understanding mode is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques. |
Data Analysis |

|
Definition--Measures of Central Tendency--Range | RangeTopicStatistics DefinitionThe range is the difference between the highest and lowest values in a data set. DescriptionThe range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data. |
Data Analysis |
|
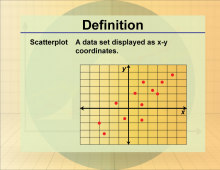
Definition--Statistics and Probability Concepts--Scatterplot | ScatterplotTopicStatistics and Probability DefinitionA scatterplot is a graphical representation of the relationship between two numerical variables. DescriptionScatterplots are essential tools in statistics for visualizing the correlation between two variables. They are widely used in fields like economics and biology to identify trends and relationships in data. For students, understanding scatterplots is important for interpreting data visually and analyzing the strength and direction of relationships between variables. This skill is crucial for developing their ability to conduct statistical analyses and draw meaningful conclusions from data. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Stem-and-Leaf Plot | Stem-and-Leaf PlotTopicStatistics and Probability DefinitionA stem-and-leaf plot is a graphical representation that organizes data points based on their place value. DescriptionStem-and-leaf plots are useful for displaying the distribution of a dataset in a concise format, preserving the original data while showing its shape. They are particularly helpful in exploratory data analysis to identify patterns and outliers. In educational settings, stem-and-leaf plots are used to teach students about data organization and visualization. Understanding this concept helps students develop skills in data interpretation and enhances their ability to summarize data effectively. |
Data Analysis |

|
Formulas--Median | Formulas--Median
The formula for the Median. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Formulas--Sum of Consecutive Integers | Formulas--Sum of Consecutive Integers
The formula for the Sum of Consecutive Integers. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Sequences and Series |

|
Formulas--Sum of Consecutive Odd Integers | Formulas--Sum of Consecutive Odd Integers
The formula for the Sum of Consecutive Integers. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Sequences and Series |

|
Definition--Charts and Graphs--Bar Graph | Definition--Charts and Graphs--Bar Graph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Box-and-Whisker Plot | Definition--Charts and Graphs--Box-and-Whisker Plot
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Circle Graph | Definition--Charts and Graphs--Circle Graph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Line Graph | Definition--Charts and Graphs--Line Graph
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Charts and Graphs--Line Plot | Definition--Charts and Graphs--Line Plot
This is a collection of definitions related to the concept of charts, graphs, and data displays. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mean | MeanTopicStatistics DefinitionThe mean is a measure of central tendency that provides an average representation of a set of data. DescriptionThe Mean is an important concept in statistics, used to summarize data effectively. In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5. |
Data Analysis |

|
Definition--Measures of Central Tendency--Median | MedianTopicStatistics DefinitionThe median is a measure of central tendency that provides the middle value of a data set.. DescriptionThe Median is an important concept in statistics, used to summarize data effectively. In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Mode | ModeTopicStatistics DefinitionThe mode is the most frequent data item.. DescriptionThe Mode is an important concept in statistics, used to summarize data effectively. It is the most frequent data item in a data set. A data set can have more than one mode. In mathematics education, understanding mode is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques. |
Data Analysis |

|
Definition--Measures of Central Tendency--Range | RangeTopicStatistics DefinitionThe range is the difference between the highest and lowest values in a data set. DescriptionThe range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data. |
Data Analysis |

|
VIDEO: Algebra Applications: Linear Functions, 3 | VIDEO: Algebra Applications: Linear Functions, 3
TopicLinear Functions DescriptionUses linear regression to analyze US oil consumption trends, projecting future usage and potential impact of Alaskan oil production. Linear functions are fundamental in understanding mathematical relationships between two variables. The video demonstrates their application in real-life scenarios, enhancing comprehension of key concepts like slope, intercepts, and graphical representation. This foundational knowledge prepares students for more advanced mathematical topics. |
Special Functions and Applications of Linear Functions |

|
MATH EXAMPLES--The Mean | MATH EXAMPLES--The Mean
This set of tutorials provides 42 examples of calculating the mean. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Median | MATH EXAMPLES--The Median
This set of tutorials provides 40 examples of calculating the median. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Mode | MATH EXAMPLES--The Mode
This set of tutorials provides 78 examples of calculating the mode. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Range | MATH EXAMPLES--The Range
This set of tutorials provides 26 examples of calculating the range. NOTE: The download is a PPT file. |
Data Analysis |

|
Math in the News: Issue 72--Box Office Flop! | Math in the News: Issue 72--Box Office Flop!
August 2013. In this issue we analyze why the movie the Lone Ranger is considered a box office flop, even though it has earned nearly $100 million. We analyze box office data. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Exponential and Logarithmic Functions, Data Analysis and Sequences |

|
Math in the News: Issue 74--Are You Driving Less? | Math in the News: Issue 74--Are You Driving Less?
August 2013. In this issue we look at the University of Michigan Study on American driving habts. The results show that Americans are driving less. But why is this? We look at the data and draw some conclusion. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 79--The End of an Era? | Math in the News: Issue 79--The End of an Era?
September 2013. In this issue we take a second look at Blackberry's financial woes. This is a follow-up report from Issue 52, where we looked at the company's revenue problems. Here we examine its final fate. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 80--A Season for the Ages | Math in the News: Issue 80--A Season for the Ages
October 2013. In this issue we follow Peyton Manning's extraordinary season with the Denver Broncos. This is a follow-up from Issue 51. This is an excellent opportunity to look at different data graphs, including box-and-whisker plots, bar graphs, and tabular data. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Math in the News: Issue 81--The Growth of America | Math in the News: Issue 81--The Growth of America
October 2013. In this issue we look at how America has grown from its formation as a country. We look at the increase in the number of states, the increase in the population, and the demographic factors that have become prominent in recent years. We look at data in tables and graphs. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |