Illustrative Math Alignment: Grade 7 Unit 8

This is a collection of Quizlet Flash Cards on various topics in Measures of Central Tendency.

Here is a collection of worksheets on various topics in Measures of Central Tendency.

This is a collection of video tutorials, transcripts, and closed captioned videos on measures of central tendency.

Overview

This collection of math examples focuses on Measures of Central Tendency, specifically the concept of Range. It comprises 26 downloadable JPG images that educators can easily incorporate into their lesson plans.

Math Worksheet Collection: Data Analysis: Mean, Median, and Mode

Overview

Overview

Overview

Overview

Overview

Overview

Here is a collection of detailed math examples on the topic of the Range.

In this TI Nspire tutorial, the Spreadsheet and Calculator windows are used to find the mean of a data list. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. .

In this video tutorial students learn how to calculate the mean when all of the data items are positive numbers. Includes three real-world examples.

In this video tutorial students learn how to calculate the mean when some of the data items are negative numbers. Includes three real-world examples.

In this video tutorial students learn how to find the median of a data set. The mean is also calculated so that students can learn similarities and differences between these two measures of central tendency. Includes three real-world examples.

In this video tutorial students learn how to calculate the mode of a data set, as well as how the mode differs from the mean and median.Includes three real-world examples.

In this video tutorial students learn about the mean of a probability distribution. Includes a brief discussion of expected value, plus a brief tie-in to weighted means. Includes three real-world examples.

In this video tutorial students learn about sample mean from a random sampling of data. All examples involve normally distributed data with a known population mean and standard deviation. Includes three real-world examples.

In this video tutorial students learn about normally distributed data and how to identify the population mean from the normal distribution. Standard deviation is briefly introduced. Includes three real-world examples.

In this video tutorial students extend their understanding of mean by looking at examples of weighted means (sometimes referred to as weighted averages). Includes three real-world examples.

In this TI Nspire tutorial, the Spreadsheet and Calculator windows are used to find the median of a data list. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. .

Topic

Statistics

Definition

The measures of central tendency is a measure of central tendency that provides an average representation of a set of data.

Description

The Measures of Central Tendency is an important concept in statistics, used to summarize data effectively.

In real-world applications, the Measures of Central Tendency helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research.

For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5.

Topic

Statistics

Definition

The average is a measure of central tendency, calculated by dividing the sum of values by their count.

Description

In statistics, the average is crucial for analyzing data sets, revealing trends, and providing insight into overall performance. It’s applicable in various fields, from school grades to business metrics. For example, if a student scores 80, 90, and 100 on three exams, the average can be calculated as follows: Average = (80 + 90 + 100) / 3 = 90. The average is essential in math education as it forms a foundational concept for more advanced statistical analyses.

Topic

Statistics

Definition

Average speed is the total distance traveled divided by the total time taken.

Description

This concept finds application in areas such as physics, transport, and everyday scenarios like calculating travel time. For example, if a car travels 300 km in 3 hours, the average speed is Average Speed = 300 km / 3 hours = 100 km/h. Understanding average speed is key in mathematics as it helps contextualize rate and distance problems in real-life situations.

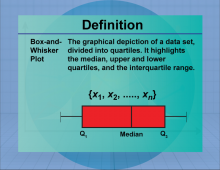
Topic

Statistics

Definition

A box-and-whisker plot is a graphical representation of data that displays the distribution through quartiles.

Description

Box-and-whisker plots are useful for visualizing the spread and skewness of a data set, highlighting the median, quartiles, and potential outliers. They are particularly valuable in comparing distributions across different groups. In real-world applications, box plots are used in quality control processes and in analyzing survey data to identify trends and anomalies.

Topic

Statistics

Definition

Categorical data refers to data that can be divided into specific categories or groups.

Description

Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.

Topic

Statistics

Definition

Continuous data is numerical data that can take any value within a range.

Description

Continuous data is vital for representing measurements such as height, weight, and temperature, which can assume an infinite number of values within a given range. In real-world applications, continuous data is used in fields like engineering, physics, and economics to model and predict outcomes. Understanding continuous data is essential for performing calculations involving integrals and derivatives in calculus.

Topic

Statistics

Definition

Discrete data consists of countable values, often represented by whole numbers.

Description

Discrete data is commonly used in situations where data points are distinct and separate, such as the number of students in a class or the number of cars in a parking lot. It is crucial for fields like computer science, where discrete structures and algorithms are fundamental. In mathematics, discrete data is used in probability theory and combinatorics, helping to solve problems involving permutations and combinations.

Topic

Statistics

Definition

The geometric mean is the nth root of the product of n numbers, used to calculate average rates of growth.

Description

The geometric mean is particularly useful in finance and economics for calculating compound interest and growth rates. Unlike the arithmetic mean, it is appropriate for data sets with values that are multiplicatively related. For example, the geometric mean of 2, 8, and 32 is calculated as (2 × 8 × 32)1/3 = 8. In mathematics, the geometric mean is essential for understanding exponential growth and decay.

Topic

Statistics

Definition

A histogram is a graphical representation of data distribution using bars of different heights.

Description

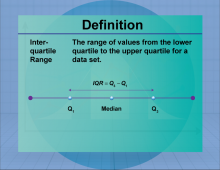
Histograms are used to visualize the frequency distribution of continuous data, making it easier to identify patterns and trends. They are widely used in fields such as economics, biology, and engineering to analyze data distributions and detect anomalies. In mathematics, histograms are essential for understanding probability distributions and statistical inference.

Topic

Statistics

Definition

The interquartile range (IQR) is the range between the first and third quartiles, representing the middle 50% of a data set.

Description

The IQR is a measure of statistical dispersion, indicating the spread of the central portion of a data set. It is particularly useful for identifying outliers and understanding the variability of data. In real-world applications, the IQR is used in finance to assess investment risks and in quality control to monitor process stability.

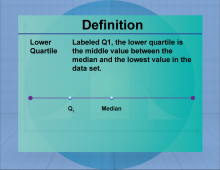
Topic

Statistics

Definition

The lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile.

Description

The lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels.

Topic

Statistics

Definition

The mean is a measure of central tendency that provides an average representation of a set of data.

Description

The Mean is an important concept in statistics, used to summarize data effectively.

In real-world applications, the Mean helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research.

For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5.

Topic

Statistics

Definition

The median is a measure of central tendency that provides the middle value of a data set..

Description

The Median is an important concept in statistics, used to summarize data effectively.

In real-world applications, the Median helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research. For large data sets, the Median provdes an average that doesn't involve the massive calculation of a mean.

Topic

Statistics

Definition

The median of an even data set is the mean of two of the terms.

Description

The Median is the middle term of a data set. If the data set consists of an even number of terms, then the Median won't be one of ther terms in the set. In such a case the Median is the Mean of the two middle terms. 

Topic

Statistics

Definition

The median of an odd data set is one of the terms in the data set.

Description

The Median is the middle term of a data set. If the data set consists of an odd number of terms, no matter how many terms there are, the Median will be the middle term of that set.

In mathematics education, understanding median of an odd data set is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.

Topic

Statistics

Definition

The mode is the most frequent data item..

Description

The Mode is an important concept in statistics, used to summarize data effectively. It is the most frequent data item in a data set. A data set can have more than one mode.

In mathematics education, understanding mode is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.

Topic

Statistics

Definition

The mode of categorical data is the most frequent item in a categorical data set.

Description

The Mode of Categorical Data is useful for finding the most frequent data item used with non-numerical data. For example, preferences for discrete characteristics can result in a mode.

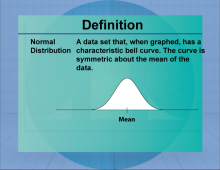
Topic

Statistics

Definition

The normal distribution is a measure of central tendency that provides an average representation of a set of data.

Description

The Normal Distribution is an important concept in statistics, used to summarize data effectively. In real-world applications, the Normal Distribution helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research.

Topic

Statistics

Definition

The outlier is is an extreme value for a data set.

Description

The Outlier is an important concept in statistics. While it doesn't represent the average data set, it does set the range of extreme values in the data set. An outlier can be extremely large or small. 

In mathematics education, understanding outlier is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.

Topic

Statistics

Definition

The population mean is a measure of central tendency that provides an average representation of a set of data.

Description

The Population Mean is an important concept in statistics, used to summarize data effectively. It is meant to represent the mean for a given statistic for an entire population. For example, the mean length of a salmon.

Topic

Statistics

Definition

A probability distribution describes how the values of a random variable are distributed.

Description

Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.

Topic

Statistics

Definition

Quartiles divide a ranked data set into four equal parts.

Description

Quartiles are used to summarize data by dividing it into four parts, each representing a quarter of the data set. They provide insight into the spread and center of data, helping to identify the distribution and variability. Quartiles are used in box plots to visually represent data distribution, making them valuable in fields such as finance and research for analyzing data trends.

Topic

Statistics

Definition

The range is the difference between the highest and lowest values in a data set.

Description

The range is a simple measure of variability that indicates the spread of a data set. It is calculated by subtracting the smallest value from the largest value, providing a quick sense of the data's dispersion. The range is used in various fields, including finance and quality control, to assess the variability and consistency of data.

Topic

Statistics

Definition

The sample mean is the average of a sample, calculated by summing the sample values and dividing by the sample size.

Description

The sample mean is a measure of central tendency that provides an estimate of the population mean based on a sample. It is widely used in statistics for making inferences about populations from samples, playing a crucial role in hypothesis testing and confidence interval estimation. The sample mean is used in fields such as economics, biology, and psychology to analyze data and draw conclusions about larger populations.

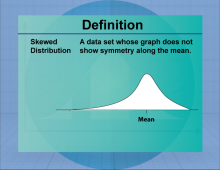
Topic

Statistics

Definition

A skewed distribution is a probability distribution that is not symmetric, with data tending to cluster more on one side.

Description

Skewed distributions occur when data is not evenly distributed around the mean, resulting in a longer tail on one side. Skewness can be positive (right-skewed) or negative (left-skewed), affecting the interpretation of data and statistical measures such as the mean and median. Skewed distributions are common in real-world data, such as income levels and test scores, where extreme values can influence the overall distribution.

Topic

Statistics

Definition

Standard deviation is a measure of the amount of variation or dispersion in a set of values.

Description

Standard deviation quantifies the degree of variation in a data set, indicating how much individual data points deviate from the mean. It is a crucial statistic for understanding the spread of data and is widely used in fields such as finance, research, and quality control to assess variability and risk. A low standard deviation indicates that data points are close to the mean, while a high standard deviation suggests greater variability.

Topic

Statistics

Definition

A symmetric distribution is a probability distribution where the left and right sides are mirror images of each other.

Description

Symmetric distributions are characterized by data that is evenly distributed around the mean, resulting in a balanced, mirror-image shape. The most common symmetric distribution is the normal distribution, which is widely used in statistics for modeling natural phenomena. Symmetric distributions are important for statistical inference, as many statistical tests assume data is symmetrically distributed.

Topic

Statistics

Definition

The upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile.

Description

The upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels.

Topic

Statistics

Definition

Variance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean.

Description

Variance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean.