
Illustrative Math Alignment: Grade 7 Unit 8
Probability and Sampling
Lesson 11: Comparing Groups
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Measures of Central Tendency--Range: Example 12 | Math Example--Measures of Central Tendency--Range: Example 12TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 34, 5, 43, 24, -48, -31, -49, 8, -41, 5, 0, 20, -41. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 92. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 13 | Math Example--Measures of Central Tendency--Range: Example 13TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 50, 18, 47, 29, 33, 27, 23, 34, 43, 17, 10, 15, 22. The solution involves arranging the numbers from least to greatest (10 to 50) and finding the difference between the two extremes. The range is calculated to be 40. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 14 | Math Example--Measures of Central Tendency--Range: Example 14TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 0, 12, -41, -47, 7, -29, -34, -24, 38, 25, 23, -9, 38, 12. The solution involves arranging the numbers from least to greatest (-47 to 38) and finding the difference between the two extremes. The range is calculated to be 85. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 15 | Math Example--Measures of Central Tendency--Range: Example 15TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 20, 13, 40, 45, 14, 2, 27, 16, 48, 43, 39, 44, 26, 12. The solution involves arranging the numbers from least to greatest (2 to 49) and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |
|
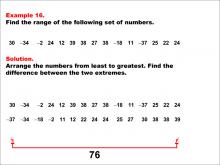
Math Example--Measures of Central Tendency--Range: Example 16 | Math Example--Measures of Central Tendency--Range: Example 16TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, -34, -2, 24, 12, 39, 38, 27, 38, -18, 11, -37, 25, 22, 24. The solution involves arranging the numbers from least to greatest (-37 to 39) and finding the difference between the two extremes. The range is calculated to be 76. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |
|
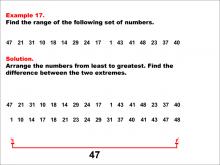
Math Example--Measures of Central Tendency--Range: Example 17 | Math Example--Measures of Central Tendency--Range: Example 17TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 47, 21, 31, 10, 18, 14, 29, 24, 17, 1, 43, 41, 48, 23, 37, 40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 18 | Math Example--Measures of Central Tendency--Range: Example 18TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: -2, -10, 24, -2, 26, 50, -40, 50, -40, 36, 30, -19, -40, 46, 27, -2. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 90. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 19 | Math Example--Measures of Central Tendency--Range: Example 19TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 14, 29, 44, 37, 9, 6, 41, 30, 19, 2, 38, 50, 26, 24, 40, 11, 45. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 2 | Math Example--Measures of Central Tendency--Range: Example 2TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 20 | Math Example--Measures of Central Tendency--Range: Example 20TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, 31, -27, 46, 25, 6, 41, 1, -27, 40, -8, -35, 9, -25, -25, -41, -38. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 87. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |
|
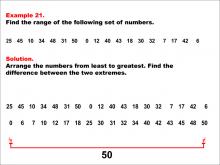
Math Example--Measures of Central Tendency--Range: Example 21 | Math Example--Measures of Central Tendency--Range: Example 21TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 25, 45, 10, 34, 48, 31, 50, 0, 12, 40, 43, 18, 30, 32, 7, 17, 42, 6. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 50. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
|
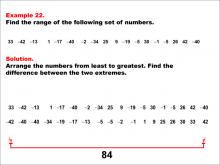
Math Example--Measures of Central Tendency--Range: Example 22 | Math Example--Measures of Central Tendency--Range: Example 22TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 33, -42, -13, 1, -17, -40, -2, -34, 25, 9, -19, -5, 30, -1, -5, 26, 42, -40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 84. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 23 | Math Example--Measures of Central Tendency--Range: Example 23TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
|
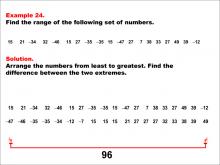
Math Example--Measures of Central Tendency--Range: Example 24 | Math Example--Measures of Central Tendency--Range: Example 24TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 15, 21, -34, 32, -46, 15, 27, -35, -35, 15, -47, 27, 7, 38, 33, 27, 49, 39, -12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 96. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 25 | Math Example--Measures of Central Tendency--Range: Example 25TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 42, 31, 16, 0, 35, 26, 30, 14, 6, 2, 13, 37, 33, 36, 19, 48, 3, 9, 45, 12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of non-negative numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 26 | Math Example--Measures of Central Tendency--Range: Example 26TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 28, 49, 1, -19, -37, 43, 27, 32, -10, 39, -19, -48, -49, 28, 36, 37, 44, 42, 29, -17. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 98. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 3 | Math Example--Measures of Central Tendency--Range: Example 3TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 4 | Math Example--Measures of Central Tendency--Range: Example 4TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 5 | Math Example--Measures of Central Tendency--Range: Example 5TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 6 | Math Example--Measures of Central Tendency--Range: Example 6TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 7 | Math Example--Measures of Central Tendency--Range: Example 7TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 8 | Math Example--Measures of Central Tendency--Range: Example 8TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 9 | Math Example--Measures of Central Tendency--Range: Example 9TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of a set of numbers: 22, 13, 15, 1, 16, 28, 3, 5, 18, 42, 8, 9. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 41. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a set of numbers and find their difference. The process encourages critical thinking and helps students visualize the relationship between numbers in a dataset. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 1 | Math Example--Measures of Central Tendency--Sample Mean--Example 1TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the sample mean for a group of 30 trout. The image displays a table showing the lengths of these trout, along with the formula for calculating the sample mean. The population of adult trout has a mean length of 15 inches with a standard deviation of 2. The sample mean is calculated by summing all the lengths (472.22 inches) and dividing by the number of trout (30), resulting in a sample mean of 15.74 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 2 | Math Example--Measures of Central Tendency--Sample Mean--Example 2TopicMeasures of Central Tendency DescriptionThis example presents another calculation of the sample mean for a group of 30 trout. The image shows a table with the lengths of these trout and the formula for the sample mean. The population of adult trout has a mean length of 15 inches with a standard deviation of 2. The sample mean is computed by adding all the lengths (436.73 inches) and dividing by the number of trout (30), yielding a sample mean of 14.56 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 3 | Math Example--Measures of Central Tendency--Sample Mean--Example 3TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the sample mean for a group of 40 trout. The image displays a table showing the lengths of these trout, along with the formula for calculating the sample mean. The population of adult trout has a mean length of 15 inches with a standard deviation of 2. The sample mean is calculated by summing all the lengths (615.86 inches) and dividing by the number of trout (40), resulting in a sample mean of 15.39 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 4 | Math Example--Measures of Central Tendency--Sample Mean--Example 4TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the sample mean for a group of 30 macaws. The image shows a table with the wingspans of these macaws and the formula for calculating the sample mean. The population of adult macaws has an average wingspan of 48 inches with a standard deviation of 6. The sample mean is computed by summing all the wingspans (1432.28 inches) and dividing by the number of macaws (30), yielding a sample mean of 47.74 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 5 | Math Example--Measures of Central Tendency--Sample Mean--Example 5TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the sample mean for another group of 30 macaws. The image displays a table showing the wingspans of these macaws, along with the formula for calculating the sample mean. The population of adult macaws has an average wingspan of 48 inches with a standard deviation of 6. The sample mean is calculated by summing all the wingspans (1398.02 inches) and dividing by the number of macaws (30), resulting in a sample mean of 46.6 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 6 | Math Example--Measures of Central Tendency--Sample Mean--Example 6TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the sample mean for a group of 30 adult male elephants. The image shows a table with the weights of these elephants and the formula for calculating the sample mean. The population of adult male elephants has an average weight of 12,000 pounds with a standard deviation of 1,500 pounds. The sample mean is computed by summing all the weights (370,924.22 pounds) and dividing by the number of elephants (30), yielding a sample mean of 12,364.14 pounds. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 7 | Math Example--Measures of Central Tendency--Sample Mean--Example 7TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the sample mean for a group of 30 mature sequoia trees. The image presents a table showing the heights of these trees, along with the formula for computing the sample mean. The population of mature sequoia trees has an average height of 220 feet with a standard deviation of 25 feet. By summing all the heights (6,844.64 feet) and dividing by the number of trees (30), we obtain a sample mean of 228.15 feet. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 1 | Math Example--Measures of Central Tendency--Weighted Mean--Example 1TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of a weighted mean for a data set consisting of the values 6, 9, and 7, with weights of 4, 5, and 6 respectively. The weighted mean is computed using the formula: (4 * 6 + 5 * 9 + 6 * 7) / (4 + 5 + 6), resulting in a final answer of 7.4. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 2 | Math Example--Measures of Central Tendency--Weighted Mean--Example 2TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of a weighted mean for a data set containing the values 1, 10, and 5, with weights of 4, 5, and 6 respectively. The weighted mean is computed using the formula: (4 * 1 + 5 * 10 + 6 * 5) / (4 + 5 + 6), resulting in a final answer of 5.6. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 3 | Math Example--Measures of Central Tendency--Weighted Mean--Example 3TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of a weighted mean for a data set containing negative and positive values: -5, 5, and 1, with weights of 4, 5, and 6 respectively. The weighted mean is computed using the formula: (4 * -5 + 5 * 5 + 6 * 1) / (4 + 5 + 6), resulting in a final answer of approximately 0.733. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 4 | Math Example--Measures of Central Tendency--Weighted Mean--Example 4TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of a weighted mean for a data set containing mostly negative values: -3, 2, and -5, with weights of 4, 3, and 5 respectively. The weighted mean is computed using the formula: (4 * -3 + 3 * 2 + 5 * -5) / (4 + 3 + 5), resulting in a final answer of approximately -2.133. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 5 | Math Example--Measures of Central Tendency--Weighted Mean--Example 5TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of a weighted mean in a real-world context, using kettlebells of different weights: 32, 24, and 16 pounds, with quantities of 4, 6, and 3 respectively. The weighted mean is computed using the formula: (4 * 32 + 6 * 24 + 3 * 16) / (4 + 6 + 3), resulting in an average weight of 24.62 pounds. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 6 | Math Example--Measures of Central Tendency--Weighted Mean--Example 6TopicMeasures of Central Tendency DescriptionThis example illustrates another real-world application of weighted mean, using kettlebells of different weights: 32, 24, and 16 pounds, with quantities of 5, 7, and 4 respectively. The weighted mean is computed using the formula: (5 * 32 + 7 * 24 + 4 * 16) / (5 + 7 + 4), resulting in an average weight of 24.5 pounds. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 7 | Math Example--Measures of Central Tendency--Weighted Mean--Example 7TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of a weighted mean using coins of different values: pennies (1 cent), nickels (5 cents), and dimes (10 cents), with quantities of 3, 2, and 4 respectively. The weighted mean is computed using the formula: (3 * 1 + 2 * 5 + 4 * 10) / (3 + 2 + 4), resulting in an average value of approximately 5.56 cents. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 8 | Math Example--Measures of Central Tendency--Weighted Mean--Example 8TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of a weighted mean using a collection of coins with different values. The image shows pennies, nickels, dimes, and quarters stacked in columns, representing quantities of 4, 3, 5, and 2 respectively. The weighted mean is computed using the formula: (4 * 1 + 3 * 5 + 5 * 10 + 2 * 25) / (4 + 3 + 5 + 2), resulting in an average value of 8.5 cents. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Weighted Mean--Example 9 | Math Example--Measures of Central Tendency--Weighted Mean--Example 9TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of a weighted mean in the context of probability, specifically finding the average sum when rolling two fair dice. The image displays a grid showing all possible outcomes of rolling two dice, with sums ranging from 2 to 12. The frequencies of each sum are highlighted in red, serving as the weights in the weighted mean calculation. The weighted mean is computed using the formula: (2 * 1 + 3 * 2 + 4 * 3 + 5 * 4 + 6 * 5 + 7 * 6 + 8 * 5 + 9 * 4 + 10 * 3 + 11 * 2 + 12 * 1) / 36, resulting in an average sum of 7. |
Data Analysis |

|
MATH EXAMPLES--The Mean | MATH EXAMPLES--The Mean
This set of tutorials provides 42 examples of calculating the mean. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Median | MATH EXAMPLES--The Median
This set of tutorials provides 40 examples of calculating the median. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Mode | MATH EXAMPLES--The Mode
This set of tutorials provides 78 examples of calculating the mode. NOTE: The download is a PPT file. |
Data Analysis |

|
MATH EXAMPLES--The Range | MATH EXAMPLES--The Range
This set of tutorials provides 26 examples of calculating the range. NOTE: The download is a PPT file. |
Data Analysis |

|
Math in the News: Issue 59--The Butterfly Migration | Math in the News: Issue 59--The Butterfly Migration
September 2012. In this issue of Math in the News we look at the great Monarch butterfly migration. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Mean of a Data Set 1 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Mean of a Data Set 2 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Mean of a Data Set 3 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Mean of a Data Set 4 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Mean of a Data Set 5 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |

|
Quizlet Flash Cards: Finding the Median of a Data Set 1 | Description This set of 10 Quizlet Flashcards covers the topic of finding the Median of a data set. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Data Analysis |