
Illustrative Math Alignment: Grade 7 Unit 8
Probability and Sampling
Lesson 15: Estimating Population Measures of Center
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Measures of Central Tendency--Upper Quartile | Upper QuartileTopicStatistics DefinitionThe upper quartile (Q3) is the median of the upper half of a data set, representing the 75th percentile. DescriptionThe upper quartile is a measure of position that indicates the value below which 75% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the upper quartile is used in finance to assess investment performance and in education to evaluate student achievement levels. |
Data Analysis |

|
Definition--Measures of Central Tendency--Variance | VarianceTopicStatistics DefinitionVariance is a measure of the dispersion of a set of values, calculated as the average of the squared deviations from the mean. DescriptionVariance quantifies the degree of spread in a data set, providing insight into the variability of data points around the mean. It is a fundamental concept in statistics, used in fields such as finance, research, and engineering to assess risk and variability. A high variance indicates greater dispersion, while a low variance suggests that data points are closer to the mean. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Average | Weighted AverageTopicStatistics DefinitionA weighted average is an average that takes into account the relative importance of each value, calculated by multiplying each value by its weight and summing the results. DescriptionThe weighted average is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted average provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Definition--Measures of Central Tendency--Weighted Mean | Weighted MeanTopicStatistics DefinitionThe weighted mean is the average of a data set where each value is multiplied by a weight reflecting its importance. DescriptionThe weighted mean is used when different data points contribute unequally to the final average. It is commonly applied in finance to calculate portfolio returns, in education to compute weighted grades, and in various fields where data points have different levels of significance. The weighted mean provides a more accurate representation of data by considering the relative importance of each value. |
Data Analysis |

|
Formulas--Mean | Formulas--Mean
The formula for the Mean. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Formulas--Median | Formulas--Median
The formula for the Median. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |

|
Interactive Math Game--DragNDrop--Measures of Central Tendency--Mean | Interactive Math Game--DragNDrop Math--Measures of Central Tendency--Mean
In this drag-and-drop game, have students practice their skills at calculating the mean of a data set. This game generates thousands of different combinations, offering an ideal opportunity for skill review in a game format. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Data Analysis |

|
Interactive Math Game--DragNDrop--Measures of Central Tendency--Median | Description
In this drag-and-drop game, have students practice their skills at calculating the median of a data set. This game generates thousands of different combinations, offering an ideal opportunity for skill review in a game format. Note: The download is the Teacher's Guide. |
Data Analysis |
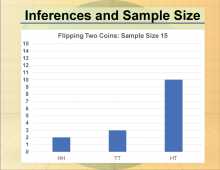
|
Math Clip Art--Statistics and Probability-- Inferences and Sample Size--10 | Math Clip Art--Statistics and Probability-- Inferences and Sample Size--10
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
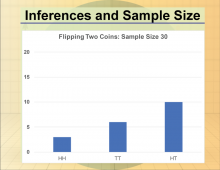
|
Math Clip Art--Statistics and Probability-- Inferences and Sample Size--11 | Math Clip Art--Statistics and Probability-- Inferences and Sample Size--11
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
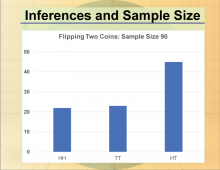
|
Math Clip Art--Statistics and Probability-- Inferences and Sample Size--12 | Math Clip Art--Statistics and Probability-- Inferences and Sample Size--12
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
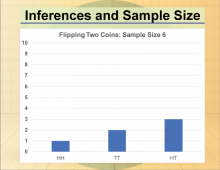
|
Math Clip Art--Statistics and Probability-- Inferences and Sample Size--9 | Math Clip Art--Statistics and Probability-- Inferences and Sample Size--9
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
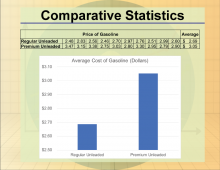
Math Clip Art--Statistics--Comparative Statistic--02 | Math Clip Art--Statistics--Comparative Statistic--02
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Analysis |
|
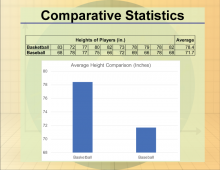
Math Clip Art--Statistics--Comparative Statistics--01 | Math Clip Art--Statistics--Comparative Statistics--01
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Analysis |
|
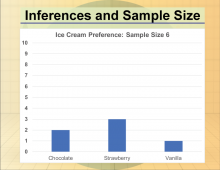
Math Clip Art--Statistics--Inferences and Sample Size--01 | Math Clip Art--Statistics--Inferences and Sample Size--01
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
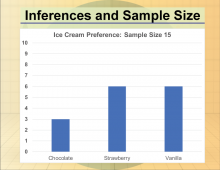
Math Clip Art--Statistics--Inferences and Sample Size--02 | Math Clip Art--Statistics--Inferences and Sample Size--02
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
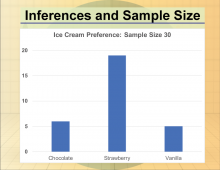
Math Clip Art--Statistics--Inferences and Sample Size--03 | Math Clip Art--Statistics--Inferences and Sample Size--03
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
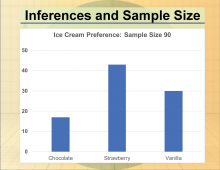
Math Clip Art--Statistics--Inferences and Sample Size--04 | Math Clip Art--Statistics--Inferences and Sample Size--04
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
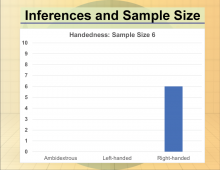
Math Clip Art--Statistics--Inferences and Sample Size--05 | Math Clip Art--Statistics--Inferences and Sample Size--05
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
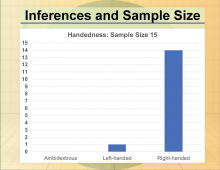
Math Clip Art--Statistics--Inferences and Sample Size--06 | Math Clip Art--Statistics--Inferences and Sample Size--06
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
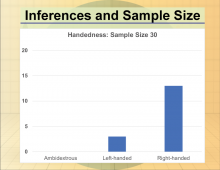
Math Clip Art--Statistics--Inferences and Sample Size--07 | Math Clip Art--Statistics--Inferences and Sample Size--07
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
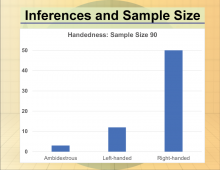
Math Clip Art--Statistics--Inferences and Sample Size--08 | Math Clip Art--Statistics--Inferences and Sample Size--08
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
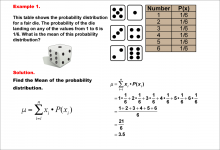
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 1 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 1TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for a probability distribution of a fair six-sided die. The probability of each outcome (1 to 6) is equally 1/6. The mean is calculated by multiplying each possible outcome by its probability and summing the results. For this fair die, the mean is determined to be 3.5. |
Data Analysis |
|
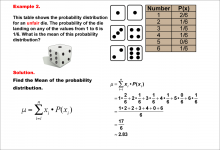
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 2 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 2TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for a probability distribution of an unfair six-sided die. Unlike a fair die, the probabilities are not equally distributed, with a higher probability (2/6) for rolling a 1. The mean is calculated using the same method as before, resulting in approximately 2.83. |
Data Analysis |
|
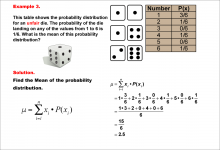
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 3 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 3TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for another unfair six-sided die. In this case, the probability of rolling a 1 is even higher (3/6), while some numbers have a probability of 0. The mean is calculated using the same method, resulting in 2.5. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 4 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 4TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for an unfair six-sided die where the number 5 has a significantly higher probability (3/6) than other numbers. The mean is calculated using the same method as previous examples, resulting in 4.5. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 5 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 5TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the probability distribution of the sum when rolling two fair dice. There are 11 possible outcomes (2 to 12), each with its own probability. The mean is calculated using the same method as previous examples, resulting in 7. |
Data Analysis |
|
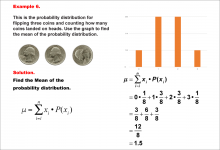
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 6 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 6TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the probability distribution of the number of heads when flipping three fair coins. The possible outcomes are 0, 1, 2, or 3 heads, each with its own probability. The mean is calculated using the same method as previous examples, resulting in 1.5. |
Data Analysis |
|
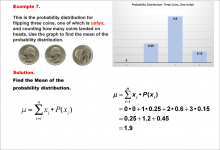
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 7 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 7TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the probability distribution of the number of heads when flipping three coins, one of which is unfair. The possible outcomes are 0, 1, 2, or 3 heads, but the probabilities are skewed due to the unfair coin. The mean is calculated using the same method as previous examples, resulting in 1.9. |
Data Analysis |
|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 1 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 1TopicMeasures of Central Tendency DescriptionThis math example demonstrates the calculation of the mean for a data set that includes negative numbers: 0, 8, 5, -5, 3, -8, 8, 4, 9, -4. The example emphasizes the step-by-step process of finding the mean, showing how to handle both positive and negative values in the calculation. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 10 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 10TopicMeasures of Central Tendency DescriptionThe image shows Example 10, demonstrating how to calculate the mean for a different set of numbers. This example illustrates finding the mean of the data set: -6, 5, -5, -5, -7, -7, -4, -1, 3. The calculation is presented step-by-step: Mean = Sum / Count. The sum of all numbers (-6 + 5 + (-5) + (-5) + (-7) + (-7) + (-4) + (-1) + 3) is divided by the count of numbers (10), resulting in -34 / 10 = -3.4. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 2 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 2TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for a dataset containing both positive and negative numbers: 7, 4, 1, 1, -1, -2, 9, 4, -9, -4. The step-by-step process shows how to sum all values, including negative ones, and divide by the total number of data points to find the mean. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 3 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 3TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for a dataset that includes negative numbers and zeros: 4, -1, 0, -2, -9, 0, -6, 5, 0, -1. The step-by-step process illustrates how to sum all values, including negatives and zeros, and divide by the total number of data points to determine the mean. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 4 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 4TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for a dataset containing both positive and negative numbers: -3, 8, 2, 1, 3, -6, -9, 3, -4. The step-by-step process demonstrates how to sum all values, including negative ones, and divide by the total number of data points to find the mean. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 5 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 5TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for a dataset that includes both positive and negative numbers: -1, 9, 3, 3, 6, -8, 8, 1, 4, 5. The step-by-step process shows how to sum all values, including negative ones, and divide by the total number of data points to determine the mean. |
Data Analysis |
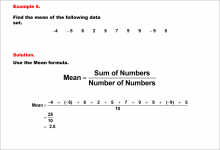
|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 6 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 6TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for a dataset containing both positive and negative numbers: -4, -5, 6, 2, 5, 7, 9, 9, -9, 5. The step-by-step process demonstrates how to sum all values, including negative ones, and divide by the total number of data points to find the mean. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 7 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 7TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for a dataset that includes negative numbers and zero: -4, 0, 2, 9, -2, -3, -5, 10, -7, 5. The step-by-step process illustrates how to sum all values, including negatives and zero, and divide by the total number of data points to determine the mean. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 8 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 8TopicMeasures of Central Tendency DescriptionThis image shows a math example calculating the mean of a data set. The numbers are: 4, 8, -6, -6, 6, -3, 4, -8, -6, -8. The solution uses the mean formula. Example 8 demonstrates finding the mean of the data set. The mean is calculated by summing all numbers and dividing by the count of numbers, resulting in (-15) / (10) = -1.5. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 9 | Math Example--Measures of Central Tendency--Mean of Data That Includes Negative Numbers--Example 9TopicMeasures of Central Tendency DescriptionThe image shows Example 9, illustrating how to find the mean of a data set using the mean formula. This example demonstrates finding the mean of the data set: -8, -9, 10, -2, 3, -2, -8, -3, 2, 5. The calculation is shown step-by-step: Mean = Sum / Count. The sum of all numbers (-8 + (-9) + 10 + (-2) + 3 + (-2) + (-8) + (-3) + 2 + 5) is divided by the count of numbers (10), resulting in -12 / 10 = -1.2. |
Data Analysis |

|
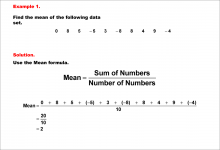
Math Example--Measures of Central Tendency--Mean: Example 1 | Math Example--Measures of Central Tendency--Mean: Example 1TopicMeasures of Central Tendency DescriptionThis example demonstrates how to calculate the mean of a dataset, a fundamental concept in statistics. The mean, often referred to as the average, is a measure of central tendency that provides insight into the typical value of a dataset. By visually presenting the calculation process, students can better grasp the concept and its application in real-world scenarios. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 10 | Math Example--Measures of Central Tendency--Mean: Example 10TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the numbers 16, 18, 0, 19, 12, 10, 7, and 20. The process involves summing all values (102) and dividing by the count of numbers (8), resulting in a mean of 12.75. This example highlights how the mean can provide a representative value for a dataset that includes both high and low numbers, including zero. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 11 | Math Example--Measures of Central Tendency--Mean: Example 11TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the numbers 9, 3, 19, 9, 15, 15, 20, 7, and 2. The process involves summing all values (99) and dividing by the count of numbers (9), resulting in a mean of 11. This example demonstrates how the mean can provide a central value that represents a dataset with repeated numbers and a wide range of values. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 12 | Math Example--Measures of Central Tendency--Mean: Example 12TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the numbers 17, 3, 10, 12, 4, 17, 7, 17, and 19. The process involves summing all values (106) and dividing by the count of numbers (9), resulting in a mean of approximately 11.78. This example showcases how the mean can provide a representative value for a dataset that includes repeated numbers and a wide range of values. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 13 | Math Example--Measures of Central Tendency--Mean: Example 13TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the numbers 13, 7, 6, 19, 12, 7, 20, 9, 12, and 15. The process involves summing all values (120) and dividing by the count of numbers (10), resulting in a mean of 12. This example demonstrates how the mean can provide a central value that represents a dataset with repeated numbers and a wide range of values. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 14 | Math Example--Measures of Central Tendency--Mean: Example 14TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the numbers 10, 2, 7, 16, 16, 17, 3, 10, 18, and 15. The process involves summing all values (114) and dividing by the count of numbers (10), resulting in a mean of 11.4. This example showcases how the mean can provide a representative value for a dataset that includes repeated numbers and a wide range of values. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 15 | Math Example--Measures of Central Tendency--Mean: Example 15TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the numbers -11, 2, 5, and -16. The process involves summing all values (-20) and dividing by the count of numbers (4), resulting in a mean of -5. This example is particularly important as it demonstrates how to handle negative numbers when calculating the mean, a concept that often challenges students. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 16 | Math Example--Measures of Central Tendency--Mean: Example 16TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the numbers -4, 18, -19, and 6. The process involves summing all values (1) and dividing by the count of numbers (4), resulting in a mean of 0.25. This example is particularly interesting as it shows how positive and negative numbers can nearly balance each other out, resulting in a mean close to zero. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 17 | Math Example--Measures of Central Tendency--Mean: Example 17TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the numbers 15, 17, -20, -5, and 18. The process involves summing all values (25) and dividing by the count of numbers (5), resulting in a mean of 5. This example is particularly instructive as it demonstrates how to handle a mix of positive and negative numbers, including some relatively large values in both directions. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 18 | Math Example--Measures of Central Tendency--Mean: Example 18TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the numbers -13, 9, 4, 14, and 8. The process involves summing all values (22) and dividing by the count of numbers (5), resulting in a mean of 4.4. This example is particularly instructive as it shows how a single negative number can significantly impact the mean, even when most of the numbers are positive. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean: Example 19 | Math Example--Measures of Central Tendency--Mean: Example 19TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the numbers 14, -7, 5, 11, -5, and 0. The process involves summing all values (18) and dividing by the count of numbers (6), resulting in a mean of 3. This example is particularly instructive as it demonstrates how to handle a mix of positive and negative numbers, including zero, in the calculation of the mean. |
Data Analysis |