edcom-728x90

IXL Ad

Illustrative Math-Media4Math Alignment

 

 

Illustrative Math Alignment: Grade 8 Unit 2

Dilations, Similarity, and Introducing Slope

Lesson 12: Using Equations for Lines

Use the following Media4Math resources with this Illustrative Math lesson.

Thumbnail Image Title Body Curriculum Topic
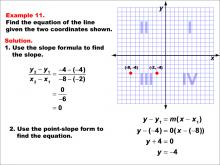
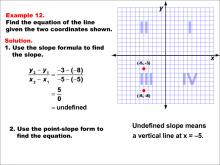
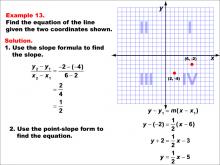
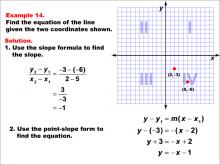
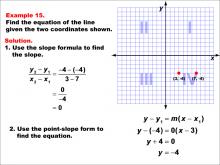
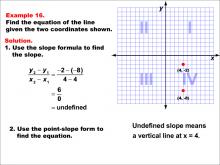
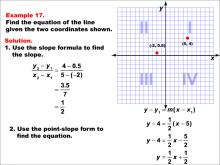
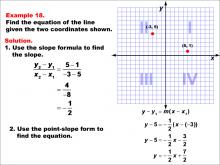
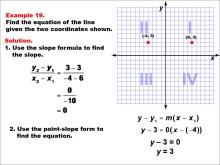
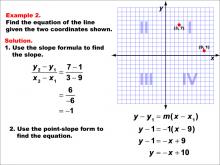
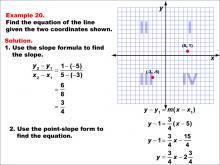
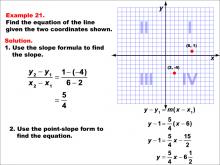
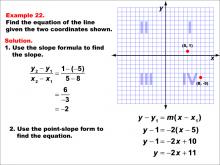
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22

Topic

Linear Functions

Description

The image shows a graph with two points (5, 1) and (8, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-5)) / (5 - 8) = -2. Using point-slope form: y - 1 = -2(x - 5), which simplifies to y = -2x + 11.

 Point-Slope Form and Slope-Intercept Form
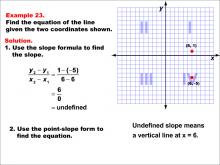
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23

Topic

Linear Functions

Description

The image shows a graph with two points (6, 1) and (6, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a vertical line using these two points. Since both x-coordinates are equal, the slope is undefined, indicating a vertical line. The slope is undefined because x-values are equal: (1 - (-5)) / (6 - 6) = undefined. This means it's a vertical line at x = 6.

 Point-Slope Form and Slope-Intercept Form
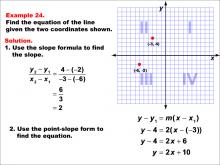
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24

Topic

Linear Functions

Description

The image shows a graph with two points (-6, -2) and (-3, 4) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (4 - (-2)) / (-3 - (-6)) = 2. Using point-slope form: y - 4 = 2(x + 3), which simplifies to y = 2x + 10.

 Point-Slope Form and Slope-Intercept Form
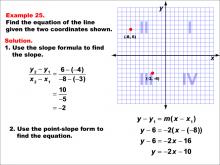
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25

Topic

Linear Functions

Description

A graph with two points (-8, 6) and (-3, -4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -2x - 10. The slope is calculated as (-4 - 6) / (-3 - (-8)) = -2. Using the point-slope form y - y1 = m(x - x1), the equation becomes y - 6 = -2(x + 8), which simplifies to y = -2x - 10.

 Point-Slope Form and Slope-Intercept Form
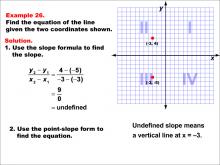
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26

Topic

Linear Functions

Description

A graph with two points (-8, -6) and (4, 2) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = 1/4 x - 3. The slope is calculated as (2 + 6) / (4 + 8) = 1/4. Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 2 = 1/4(x - 4), which simplifies to y = 1/4 x - 3.

 Point-Slope Form and Slope-Intercept Form
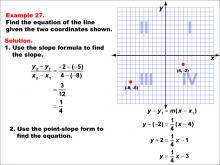
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27

Topic

Linear Functions

Description

A graph with two points (-3, 4) and (-3, -5) marked on a coordinate plane. The slope is undefined because both x-coordinates are equal, leading to division by zero. This represents a vertical line at x = -3. The slope is undefined because (4 + 5) / (-3 + 3) results in division by zero. This indicates a vertical line at x = -3.

 Point-Slope Form and Slope-Intercept Form
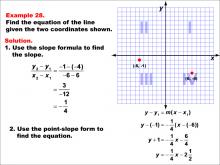
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28

Topic

Linear Functions

Description

A graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2).

 Point-Slope Form and Slope-Intercept Form
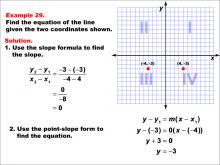
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29

Topic

Linear Functions

 Point-Slope Form and Slope-Intercept Form
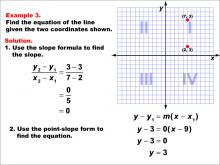
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3

Topic

Linear Functions

Description

This example demonstrates how to find the equation of a horizontal line passing through the points (2, 3) and (7, 3). The slope is calculated as 0 since both y-coordinates are the same. Using the point-slope form, y - y1 = m(x - x1), the equation becomes y - 3 = 0(x - any x-value), which simplifies to y = 3, representing a horizontal line.

 Point-Slope Form and Slope-Intercept Form
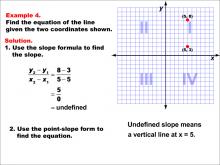
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4

Topic

Linear Functions

Description

This example illustrates how to find the equation of a vertical line passing through the points (5, 3) and (5, 8). The slope is undefined because both x-coordinates are the same, resulting in division by zero when using the slope formula. This indicates a vertical line, and the equation is simply x = 5.

 Point-Slope Form and Slope-Intercept Form
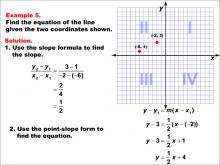
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5

Topic

Linear Functions

Description

This example demonstrates how to find the equation of a line passing through the points (-6, 1) and (-2, 3). The slope is calculated using the formula (y2 - y1) / (x2 - x1), resulting in a slope of 1/2. Using the point-slope form of a line, y - y1 = m(x - x1), the equation is derived and simplified to y = (1/2)x + 4.

 Point-Slope Form and Slope-Intercept Form
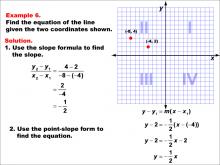
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6

Topic

Linear Functions

Description

This image shows a graph with two points (-8, 4) and (-4, 2). The slope is calculated as (y2 - y1) / (x2 - x1), resulting in a slope of -1/2. The equation of the line is derived using point-slope form and simplified to y = -(1/2)x. The slope is calculated as -1/2, and the line equation is determined using point-slope form: y = -(1/2)x.

 Point-Slope Form and Slope-Intercept Form
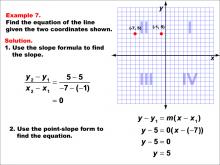
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7

Topic

Linear Functions

Description

This image shows a graph with two points (-7, 5) and (-1, 5). The slope is calculated as zero since the y-values are equal. The equation of the line is horizontal, simplified to y = 5. The slope is 0, indicating a horizontal line. The equation is y = 5.

 Point-Slope Form and Slope-Intercept Form
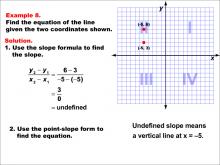
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8

Topic

Linear Functions

Description

This image shows a graph with two points (-5, 6) and (-5, 3). The slope is undefined because the x-values are equal. This results in a vertical line at x = -5. The slope is undefined, indicating a vertical line at x = -5.

 Point-Slope Form and Slope-Intercept Form
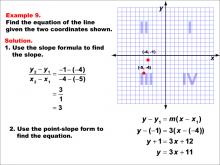
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9

Topic

Linear Functions

Description

The image shows a coordinate plane with two points (-5, -4) and (-4, -1) marked. It provides a step-by-step solution to find the equation of the line passing through these points. The slope is calculated, and the equation is derived using point-slope form. The slope is calculated as (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (-4 - (-5)) = 3 / 1 = 3. Using point-slope form, y - y1 = m(x - x1), the equation is derived as y + 1 = 3(x + 4), which simplifies to y = 3x + 11.

 Point-Slope Form and Slope-Intercept Form
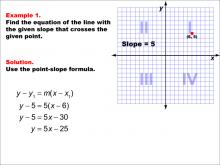
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 1 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 1 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 1

Topic

The Point-Slope Form

Description

This example demonstrates how to find the equation of a line using the point-slope form. The given information includes a slope of 5 and a point (6, 5) through which the line passes. Using the point-slope formula y - y1 = m(x - x1), we can substitute the known values to derive the equation y - 5 = 5(x - 6). Simplifying this equation leads to the final result: y = 5x - 25.

 Point-Slope Form
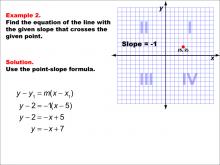
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 2 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 2 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 2

Topic

The Point-Slope Form

Description

In this example, we explore finding the equation of a line with a slope of -1 passing through the point (5, 2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 2 = -(x - 5). After simplification, the final equation of the line is y = -x + 7.

 Point-Slope Form
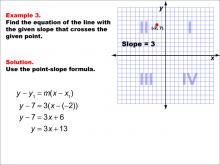
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 3 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 3 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 3

Topic

The Point-Slope Form

Description

This example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 3 passing through the point (-2, 7). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - 7 = 3(x - (-2)). After simplification, the resulting equation is y = 3x + 13.

 Point-Slope Form
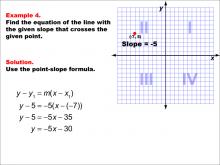
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4

Topic

The Point-Slope Form

Description

In this example, we explore finding the equation of a line with a slope of -5 that passes through the point (-7, 5). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 5 = -5(x - (-7)). After simplification, the final equation of the line is y = -5x - 30.

 Point-Slope Form
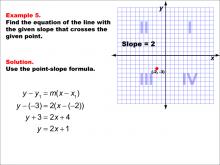
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5

Topic

The Point-Slope Form

Description

This example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 2 passing through the point (-2, -3). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-3) = 2(x - (-2)). After simplification, the resulting equation is y = 2x + 1.

 Point-Slope Form
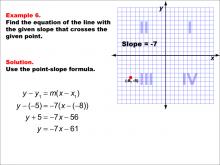
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6

Topic

The Point-Slope Form

Description

This example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -7 passing through the point (-8, -5). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-5) = -7(x - (-8)). After simplification, the resulting equation is y = -7x - 61.

 Point-Slope Form
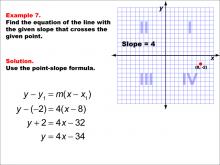
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7

Topic

The Point-Slope Form

Description

In this example, we explore finding the equation of a line with a slope of 4 passing through the point (8, -2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - (-2) = 4(x - 8). After simplification, the final equation of the line is y = 4x - 34.

 Point-Slope Form
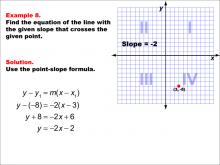
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8

Topic

The Point-Slope Form

Description

This example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -2 passing through the point (3, -8). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-8) = -2(x - 3). After simplification, the resulting equation is y = -2x - 2.

 Point-Slope Form
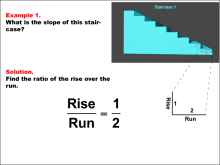
Math Examples Math Example: The Slope As Rise Over Run: Three Examples

In this set of math examples, see how slope is calculated for a staircase based on measures for the rise and the run.

 Slope
MATH EXAMPLES--Teacher's Guide: Finding the Equation of a Line, Given Two Points MATH EXAMPLES--Teacher's Guide: Finding the Equation of a Line, Given Two Points MATH EXAMPLES--Teacher's Guide: Finding the Equation of a Line, Given Two Points

This Teacher's Guide provides an overview of the 12 worked-out examples that show how to find the equation of a line, given two points.

This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

 Applications of Linear Functions and Graphs of Linear Functions
MATH EXAMPLES--Teacher's Guide: Graphs of Linear Functions in Slope-Intercept Form MATH EXAMPLES--Teacher's Guide: Graphs of Linear Functions in Slope-Intercept Form MATH EXAMPLES--Teacher's Guide: Graphs of Linear Functions in Slope-Intercept Form

This Teacher's Guide provides an overview of the 13 worked-out examples that show how to graph a linear function, given the slope and y-intercept.

This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

 Applications of Linear Functions and Graphs of Linear Functions
MATH EXAMPLES--Teacher's Guide: The Midpoint Formula MATH EXAMPLES--Teacher's Guide: The Midpoint Formula MATH EXAMPLES--Teacher's Guide: The Midpoint Formula

This Teacher's Guide provides an overview of the 20 worked-out examples that show how to use the Midpont Formula.

This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

 Midpoint Formula
MATH EXAMPLES--Teacher's Guide: The Point Slope Form MATH EXAMPLES--Teacher's Guide: The Point Slope Form MATH EXAMPLES--Teacher's Guide: The Point Slope Form

This Teacher's Guide provides an overview of the 8 worked-out examples that show how to find the equation of a lineusing the Point Slope Form.

This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

 Applications of Linear Functions and Graphs of Linear Functions
MATH EXAMPLES--Teacher's Guide: The Slope Formula MATH EXAMPLES--Teacher's Guide: The Slope Formula MATH EXAMPLES--Teacher's Guide: The Slope Formula

This Teacher's Guide provides an overview of the 21 worked-out examples that show how to use the Slope Formula.

This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

 Applications of Linear Functions and Slope
MATH EXAMPLES--Teacher's Guide: Transformations MATH EXAMPLES--Teacher's Guide: Transformations MATH EXAMPLES--Teacher's Guide: Transformations

This set of tutorials provides 56 examples of transformations of geometric figures on a graph.

This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

 Applications of Transformations and Definition of Transformations
MATH EXAMPLES--The Slope Formula MATH EXAMPLES--The Slope Formula MATH EXAMPLES--The Slope Formula

The complete set of 21 examples that make up this set of tutorials. NOTE: The download is a PPT file.

 Applications of Linear Functions and Slope
MATH EXAMPLES--Transformations MATH EXAMPLES--Transformations MATH EXAMPLES--Transformations

This set of tutorials provides 56 examples of transformations of geometric figures on a graph. NOTE: The download is a PPT file.

 Applications of Transformations and Definition of Transformations
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Easy) Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Easy) Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Easy)

This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Point-Slope Form and Slope-Intercept Form
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Hard) Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Hard) Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Hard)

This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Point-Slope Form and Slope-Intercept Form
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Medium) Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Medium) Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Medium)

This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Point-Slope Form and Slope-Intercept Form
Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy) Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy) Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy)

This is part of a collection of math quizzes on the topic of Linear Equations.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Slope-Intercept Form
Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard) Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard) Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard)

This is part of a collection of math quizzes on the topic of Linear Equations.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Slope-Intercept Form
Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium) Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium) Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium)

This is part of a collection of math quizzes on the topic of Linear Equations.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Slope-Intercept Form
Paper-and-Pencil Quiz: Slope Formula (Easy) Paper-and-Pencil Quiz: Slope Formula (Easy) Paper-and-Pencil Quiz: Slope Formula (Easy)

This is part of a collection of math quizzes on the topic of the Slope Formula.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Slope
Paper-and-Pencil Quiz: Slope Formula (Hard) Paper-and-Pencil Quiz: Slope Formula (Hard) Paper-and-Pencil Quiz: Slope Formula (Hard)

This is part of a collection of math quizzes on the topic of the Slope Formula.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Slope
Paper-and-Pencil Quiz: Slope Formula (Medium) Paper-and-Pencil Quiz: Slope Formula (Medium) Paper-and-Pencil Quiz: Slope Formula (Medium)

This is part of a collection of math quizzes on the topic of the Slope Formula.

To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Quiz Library

To see the complete collection of Quizzes, click on this link.

ary">click on this link.

 Slope
Promethean Flipchart: Algebra Jeopardy In this Promethean Flipchart, review key concepts from linear functions using a Jeopardy-style game. Note: The download for this resources is the Promethean Flipchart. Applications of Equations and Inequalities
Promethean Flipchart: Geometry Applications: Transformations 1

Roller coasters provide an ideal opportunity to explore translations and rotations. Displacement vectors are also introduced. Note: The download for this resources is the Promethean Flipchart.

To access the full video [Geometry Applications: Transformations, Segment 1: Translations and Rotations]: https://www.media4math.com/library/geometry-applications-transformations-segment-1-translations-and-rotations

This video includes a video transcript: https://media4math.com/library/video-transcript-geometry-applications-transformations-segment-1-translations-and-rotations

 Applications of Transformations
Promethean Flipchart: Geometry Applications: Transformations 2

Cargo ships transport tons of merchandise from one country to another and accounts for most of the global economy. Loading and unloading these ships requires a great deal of organization and provides an ideal example of three-dimensional translations. Note: The download for this resources is the Promethean Flipchart.

To access the full video [Geometry Applications: Transformations, Segment 2: 3D Translations]: https://www.media4math.com/library/geometry-applications-transformations-segment-2-3d-translations

This video includes a video transcript: https://media4math.com/library/video-transcript-geometry-applications-transformations-segment-2-3d-translations

 Applications of Transformations
Promethean Flipchart: Geometry Applications: Transformations 3

The Gemini telescope in Hawaii is an example of architecture that moves. All observatories rotate in order to follow objects in the sky. This also provides an opportunity to explore rotations, reflections, and symmetry. Note: The download for this resources is the Promethean Flipchart.

The full video [Geometry Applications: Transformations, Segment 3: Rotations, Reflections, and Symmetry] can be found here: https://media4math.com/library/geometry-applications-transformations-segment-3-rotations-reflections-and-symmetry

 Applications of Transformations
QuizletFlashCards.jpg Quizlet Flash Cards: Slope Formula, Set 01

Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 		Slope
QuizletFlashCards.jpg Quizlet Flash Cards: Slope Formula, Set 02

Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 		Slope
QuizletFlashCards.jpg Quizlet Flash Cards: Slope Formula, Set 03

Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 		Slope
QuizletFlashCards.jpg Quizlet Flash Cards: Slope Formula, Set 04

Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 		Slope
QuizletFlashCards.jpg Quizlet Flash Cards: Slope Formula, Set 05

Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 		Slope