
Illustrative Math Alignment: Grade 8 Unit 8
Pythagorean Theorem and Irrational Numbers
Lesson 10: Applications of the Pythagorean Theorem
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
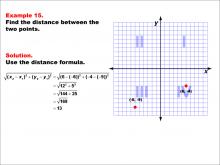
Math Example--Coordinate Geometry--Distance Formula: Example 15 | Math Example--Coordinate Geometry--Distance Formula: Example 15TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-6, -9) and (6, -4) are plotted on a graph, and the distance between them is calculated using the formula: √((6 - (-6))2 + (-4 - (-9))2) = √(122 + 52) = 13. |
The Distance Formula |
|
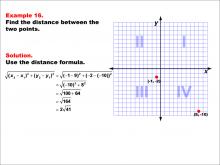
Math Example--Coordinate Geometry--Distance Formula: Example 16 | Math Example--Coordinate Geometry--Distance Formula: Example 16TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-1, -2) and (9, -10) are plotted on a graph, and the distance between them is determined using the formula: √((-1 - 9)2 + (-2 - (-10))2) = √((-10)2 + 82) = 2√41. |
The Distance Formula |
|
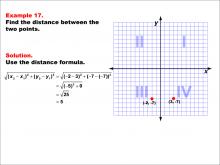
Math Example--Coordinate Geometry--Distance Formula: Example 17 | Math Example--Coordinate Geometry--Distance Formula: Example 17TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the horizontal distance between two points on a coordinate plane. The points (-2, -7) and (3, -7) are plotted on a graph, and the distance between them is calculated using the formula: √((-2 - 3)2 + (-7 + 7)2) = √((-5)2 + 0) = 5. |
The Distance Formula |
|
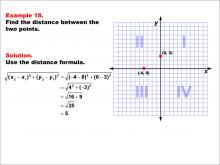
Math Example--Coordinate Geometry--Distance Formula: Example 18 | Math Example--Coordinate Geometry--Distance Formula: Example 18TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-4, 0) and (0, 3) are plotted on a graph, and the distance between them is determined using the formula: √((4 - 0)2 + (0 - 3)2) = √(16 + 9) = 5. |
The Distance Formula |
|
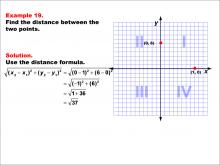
Math Example--Coordinate Geometry--Distance Formula: Example 19 | Math Example--Coordinate Geometry--Distance Formula: Example 19TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (0, 6) and (1, 0) are plotted on a graph, and the distance between them is calculated using the formula: √((0 - 1)2 + (6 - 0)2) = √(1 + 36) = √37. |
The Distance Formula |
|
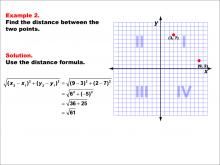
Math Example--Coordinate Geometry--Distance Formula: Example 2 | Math Example--Coordinate Geometry--Distance Formula: Example 2TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (3, 7) and (9, 2) are plotted on a graph, and the distance between them is determined using the formula: √((9 - 3)2 + (2 - 7)2) = √(61). |
The Distance Formula |
|
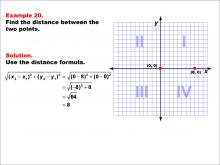
Math Example--Coordinate Geometry--Distance Formula: Example 20 | Math Example--Coordinate Geometry--Distance Formula: Example 20TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the horizontal distance between two points on a coordinate plane. The points (0, 0) and (8, 0) are plotted on a graph, and the distance between them is determined using the formula: √((0 - 8)2 + (0 - 0)2) = √64 = 8. |
The Distance Formula |
|
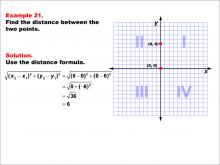
Math Example--Coordinate Geometry--Distance Formula: Example 21 | Math Example--Coordinate Geometry--Distance Formula: Example 21TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the vertical distance between two points on a coordinate plane. The points (0, 0) and (0, 6) are plotted on a graph, and the distance between them is calculated using the formula: √((0 - 0)2 + (0 - 6)2) = √(0 + (-6)2) = 6. |
The Distance Formula |
|
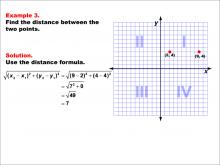
Math Example--Coordinate Geometry--Distance Formula: Example 3 | Math Example--Coordinate Geometry--Distance Formula: Example 3TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (2, 4) and (9, 4) are plotted on a graph, and the distance between them is calculated using the formula: √((9 - 2)2 + (4 - 4)2) = 7. |
The Distance Formula |
|
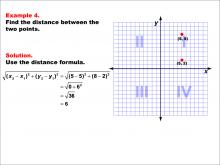
Math Example--Coordinate Geometry--Distance Formula: Example 4 | Math Example--Coordinate Geometry--Distance Formula: Example 4TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the vertical distance between two points on a coordinate plane. The points (5, 8) and (5, 2) are plotted on a graph, and the distance between them is determined using the formula: √((5 - 5)2 + (8 - 2)2) = 6. |
The Distance Formula |
|
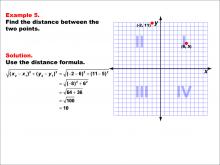
Math Example--Coordinate Geometry--Distance Formula: Example 5 | Math Example--Coordinate Geometry--Distance Formula: Example 5TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-2, 11) and (6, 5) are plotted on a graph, and the distance between them is calculated using the formula: √((-2 - 6)2 + (11 - 5)2) = 10. |
The Distance Formula |
|
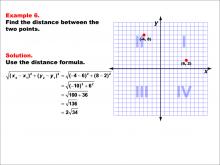
Math Example--Coordinate Geometry--Distance Formula: Example 6 | Math Example--Coordinate Geometry--Distance Formula: Example 6TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-4, 8) and (6, 2) are plotted on a graph, and the distance between them is determined using the formula: √((-4 - 6)2 + (8 - 2)2) = 2 √(34). |
The Distance Formula |
|
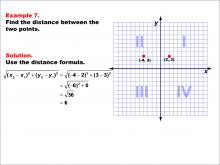
Math Example--Coordinate Geometry--Distance Formula: Example 7 | Math Example--Coordinate Geometry--Distance Formula: Example 7TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-4, 3) and (2, 3) are plotted on a graph, and the distance between them is calculated using the formula: √((-4 - 2)2 + (3 - 3)2) = 6. |
The Distance Formula |
|
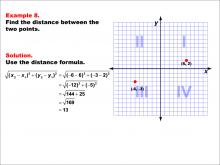
Math Example--Coordinate Geometry--Distance Formula: Example 8 | Math Example--Coordinate Geometry--Distance Formula: Example 8TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-6, -3) and (6, 2) are plotted on a graph, and the distance between them is determined using the formula: √((-6 - 6)2 + (-3 - 2)2) = 13. |
The Distance Formula |
|
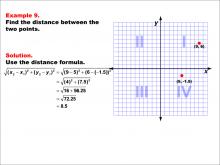
Math Example--Coordinate Geometry--Distance Formula: Example 9 | Math Example--Coordinate Geometry--Distance Formula: Example 9TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (9, 6) and (5, -1.5) are plotted on a graph, and the distance between them is calculated using the formula: √((9 - 5)2 + (6 - (-1.5))2) = √(4^2 + 7.5^2) = √72.25 = 8.5. |
The Distance Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 1 | Calculating the Discriminant: Example 1TopicQuadratics |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 10 | Calculating the Discriminant: Example 10TopicQuadratics DescriptionThis example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real solutions to the equation. This scenario helps students recognize the significance of repeated roots and their graphical representation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 2 | Calculating the Discriminant: Example 2TopicQuadratics |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 3 | Calculating the Discriminant: Example 3TopicQuadratics DescriptionThis example demonstrates a quadratic equation with one distinct real root, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 4 | Calculating the Discriminant: Example 4TopicQuadratics DescriptionThis example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real roots. This scenario helps students recognize the significance of repeated roots and their graphical representation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 5 | Calculating the Discriminant: Example 5TopicQuadratics DescriptionThis example demonstrates a quadratic equation with no distinct real roots, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 6 | Calculating the Discriminant: Example 6TopicQuadratics DescriptionThis example illustrates a quadratic with a double real root. The discriminant being zero indicates that there is exactly one real solution to the equation. This scenario helps students recognize the significance of repeated roots and their graphical representation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 7 | Calculating the Discriminant: Example 7TopicQuadratics DescriptionIn this example, the quadratic equation results in two roots, demonstrating the cases where the discriminant is positive. This provides insights into scenarios where quadratic equations intersect the x-axis twice. Skills in algebra are focused on interpreting complex solutions and their geometric implications. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 8 | Calculating the Discriminant: Example 8TopicQuadratics DescriptionThis example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real solutions to the equation. This scenario helps students recognize the significance of two roots and their graphical representation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Quadratic Formula |

|
Math Example--Quadratics--Calculating the Discriminant: Example 9 | Calculating the Discriminant: Example 9TopicQuadratics DescriptionThis example demonstrates a quadratic equation with two distinct real roots, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection. |
Quadratic Formula |
|
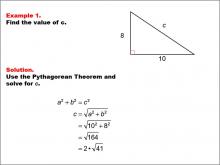
Math Example--Right Triangles-- Example 1 | Math Example--Right Triangles-- Example 1TopicRight Triangles DescriptionThis example presents a right triangle with sides of length 8 and 10, and an unknown hypotenuse labeled c. The task is to find the value of c using the Pythagorean Theorem. By applying the formula a2 + b2 = c2, we can calculate that c = √(102 + 82) = √(164) = 2 * √(41). |
Right Triangles |
|
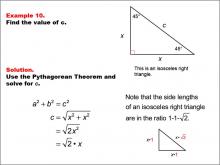
Math Example--Right Triangles-- Example 10 | Math Example--Right Triangles-- Example 10TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 11 | Math Example--Right Triangles-- Example 11TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 12 | Math Example--Right Triangles-- Example 12TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 13 | Math Example--Right Triangles-- Example 13TopicRight Triangles |
Right Triangles |
|
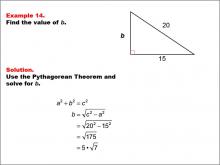
Math Example--Right Triangles-- Example 14 | Math Example--Right Triangles-- Example 14TopicRight Triangles |
Right Triangles |
|
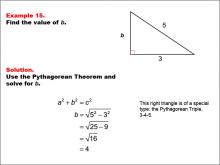
Math Example--Right Triangles-- Example 15 | Math Example--Right Triangles-- Example 15TopicRight Triangles |
Right Triangles |
|
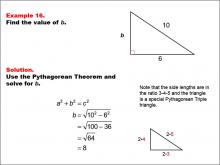
Math Example--Right Triangles-- Example 16 | Math Example--Right Triangles-- Example 16TopicRight Triangles |
Right Triangles |
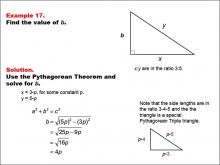
|
Math Example--Right Triangles-- Example 17 | Math Example--Right Triangles-- Example 17TopicRight Triangles |
Right Triangles |
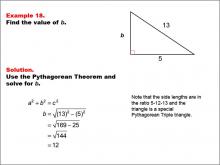
|
Math Example--Right Triangles-- Example 18 | Math Example--Right Triangles-- Example 18TopicRight Triangles |
Right Triangles |
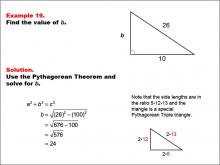
|
Math Example--Right Triangles-- Example 19 | Math Example--Right Triangles-- Example 19TopicRight Triangles |
Right Triangles |
|
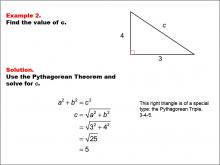
Math Example--Right Triangles-- Example 2 | Math Example--Right Triangles-- Example 2TopicRight Triangles DescriptionIn this example, we have a right triangle with sides of length 3 and 4, and an unknown hypotenuse labeled c. The goal is to determine the value of c using the Pythagorean Theorem. By applying the formula a2 + b2 = c2, we can calculate that c = √(32 + 42) = √(25) = 5. This example builds upon the previous one, reinforcing the application of the Pythagorean Theorem in right triangles. It demonstrates how the theorem can be used with different side lengths, helping students understand its versatility in solving various right triangle problems. |
Right Triangles |
|
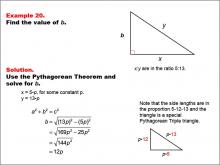
Math Example--Right Triangles-- Example 20 | Math Example--Right Triangles-- Example 20TopicRight Triangles |
Right Triangles |
|
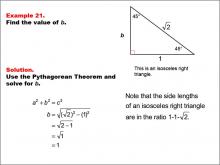
Math Example--Right Triangles-- Example 21 | Math Example--Right Triangles-- Example 21TopicRight Triangles |
Right Triangles |
|
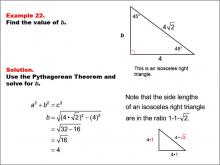
Math Example--Right Triangles-- Example 22 | Math Example--Right Triangles-- Example 22TopicRight Triangles |
Right Triangles |
|
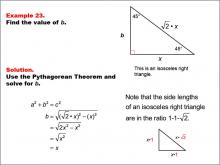
Math Example--Right Triangles-- Example 23 | Math Example--Right Triangles-- Example 23TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 24 | Math Example--Right Triangles-- Example 24TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 25 | Math Example--Right Triangles-- Example 25TopicRight Triangles |
Right Triangles |

|
Math Example--Right Triangles-- Example 26 | Math Example--Right Triangles-- Example 26TopicRight Triangles |
Right Triangles |
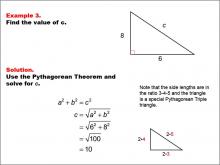
|
Math Example--Right Triangles-- Example 3 | Math Example--Right Triangles-- Example 3TopicRight Triangles |
Right Triangles |
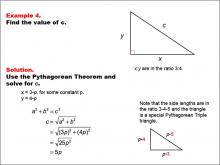
|
Math Example--Right Triangles-- Example 4 | Math Example--Right Triangles-- Example 4TopicRight Triangles |
Right Triangles |
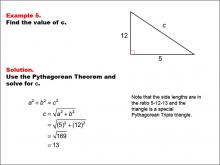
|
Math Example--Right Triangles-- Example 5 | Math Example--Right Triangles-- Example 5TopicRight Triangles |
Right Triangles |
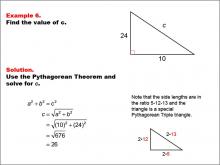
|
Math Example--Right Triangles-- Example 6 | Math Example--Right Triangles-- Example 6TopicRight Triangles |
Right Triangles |
|
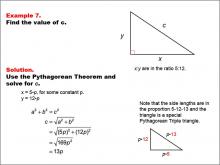
Math Example--Right Triangles-- Example 7 | Math Example--Right Triangles-- Example 7TopicRight Triangles |
Right Triangles |
|
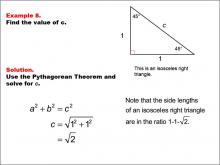
Math Example--Right Triangles-- Example 8 | Math Example--Right Triangles-- Example 8TopicRight Triangles |
Right Triangles |