
Illustrative Math Alignment: Grade 6 Unit 3
Unit Rates and Percentages
Lesson 8: More about Constant Speed
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 01 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 01TopicQuadratics DescriptionThis image features a vintage car in motion with a blurred background, emphasizing speed. It serves as an introduction to the series on speed and acceleration in linear and quadratic functions. The image visually represents the concept of speed through motion blur, making it relatable for students learning about linear functions. By using this image, teachers can engage students with real-world applications of mathematical concepts. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
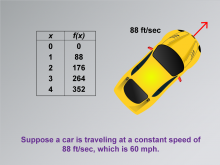
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 02 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 02TopicQuadratics DescriptionThis image depicts a yellow car alongside a table that shows time in seconds and distance in feet, illustrating a constant speed of 88 ft/sec (60 mph). The table provides a clear example of how linear functions can represent constant speeds. Teachers can use this image to demonstrate the relationship between time, distance, and speed, reinforcing the concept of constant rates within linear functions. |
Graphs of Linear Functions and Graphs of Quadratic Functions |

|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 03 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 03TopicQuadratics DescriptionThis image is a variation of the previous image that highlights the common difference as the rate of speed. It builds on the previous example by emphasizing how the common difference (88 ft/sec) serves as the rate in linear equations. This visual representation helps students grasp how mathematical differences translate into real-world speeds. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
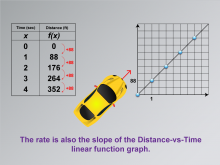
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 04 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 04TopicQuadratics DescriptionThis image presents a table with time in seconds and distance in feet, accompanied by a graph illustrating a linear relationship between time and distance. The constant increase of 88 feet per second is depicted as the slope of the Distance-vs-Time linear function graph. This visual aids students in understanding how linear functions can model real-world speed scenarios. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
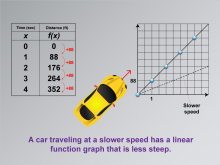
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 05 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 05TopicQuadratics DescriptionThis image is a variation showing time and distance data with a graph that includes a dotted line labeled "Slower speed." The graph illustrates how different speeds affect the steepness of linear function graphs. This visual comparison helps students see how speed variations are represented mathematically. Using math clip art allows students to visualize differences in speed through graphical representations, aiding comprehension of linear functions' applications. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
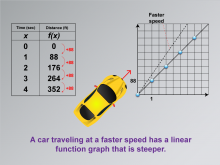
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 06 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 06TopicQuadratics DescriptionThis image shows a graph similar to the previous one but with a steeper dotted line labeled "Faster speed." It visually demonstrates how increased speed results in a steeper slope on a linear function graph. This helps students understand the relationship between speed changes and their graphical representations. The use of math clip art facilitates learning by providing clear visual examples that connect mathematical concepts to real-world scenarios. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
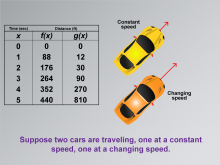
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 07 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 07TopicQuadratics DescriptionThis image displays a table with time and distance data for two functions, f(x) representing constant speed, and g(x) representing changing speed. Two car icons illustrate these concepts visually. This comparison allows students to explore how different types of motion are modeled mathematically. The use of math clip art aids in understanding complex concepts by providing relatable visual examples that highlight differences in mathematical functions. |
Graphs of Linear Functions and Graphs of Quadratic Functions |

|
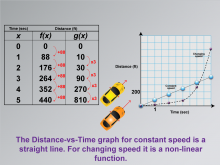
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 08 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 08TopicQuadratics DescriptionThis image presents time-distance data for functions f(x) with constant increments, showing constant speed, while g(x) shows changing speed with a common ratio. The visual representation helps students understand different mathematical relationships through real-world examples. The use of math clip art enhances comprehension by clearly illustrating abstract concepts like common differences versus common ratios in mathematical functions. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 09 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 09TopicQuadratics DescriptionThis image features a graph comparing linear and non-linear functions, illustrating constant and changing speeds. The visual contrast between the two types of functions helps students understand how different speeds are modeled mathematically. The linear function represents constant speed, while the non-linear function shows acceleration or deceleration. Math clip art like this is crucial for teaching because it provides visual clarity, helping students differentiate between linear and quadratic functions in real-world contexts. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
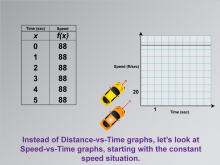
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 10 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 10TopicQuadratics DescriptionThis image illustrates a constant speed through a graph that shows a straight line, representing uniform motion. It provides an opportunity for students to see how consistent motion is represented visually in a linear function. The consistent slope indicates constant speed, making it easier for students to connect mathematical concepts with practical applications. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
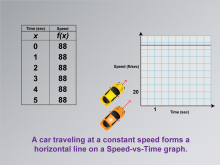
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 11 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 11TopicQuadratics DescriptionThis image shows a graph and data for a constant speed scenario. The graph helps students understand how different speeds are represented in mathematical models, with linear sections indicating constant speed and curved sections showing acceleration or deceleration. Math clip art like this is essential for teaching as it visually differentiates between linear and quadratic functions, providing clarity in understanding real-world applications. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
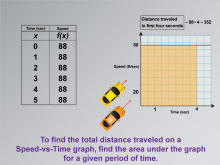
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 12 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 12TopicQuadratics DescriptionThis image includes a Speed-vs-Time graph with an area under the curve highlighted to represent distance traveled over time. The calculation for distance (88 * 4 = 352) is shown, helping students visualize how to determine total distance using graphs. The use of math clip art enhances learning by providing visual context for abstract concepts like integration in real-world scenarios. Teacher's Script: "See the shaded area? It represents distance. How do we calculate it? Let's find out." |
Graphs of Linear Functions and Graphs of Quadratic Functions |
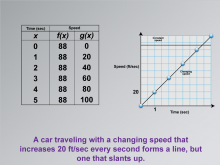
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 13 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 13TopicQuadratics DescriptionThis image shows a graph displaying two lines: a horizontal line for constant speed and a slanted line for changing speed. It illustrates how different speeds are represented graphically, helping students understand the concept of acceleration. The use of math clip art provides clarity by visually differentiating between constant and changing speeds, aiding comprehension. Teacher's Script: "Look at these lines. How do they show different speeds? Let's explore what these shapes tell us." |
Graphs of Linear Functions and Graphs of Quadratic Functions |
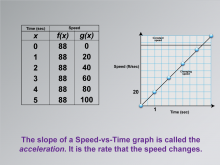
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 14 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 14TopicQuadratics DescriptionThis image includes a table with time (x) and speed (f(x) and g(x)). The graph shows constant and changing speeds, emphasizing the slope. The slope of a Speed-vs-Time graph is called acceleration, which is the rate that speed changes. The use of math clip art helps students visualize how acceleration is represented graphically, aiding in understanding real-world applications. Teacher's Script: "Notice the slope of these lines. How does it show acceleration? Let's explore what this means for speed changes." |
Graphs of Linear Functions and Graphs of Quadratic Functions |
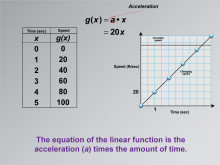
|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 15 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 15TopicQuadratics DescriptionThis image presents a table with time (x) and speed (g(x)). The graph emphasizes acceleration as the slope, with an equation showing g(x) = 20x. The equation of the linear function is the acceleration (a) times the amount of time. The use of math clip art clarifies how equations relate to real-world motion, enhancing comprehension. Teacher's Script: "See how the equation shows acceleration? What does the slope tell us about speed changes?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
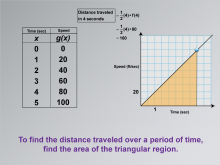
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 16 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 16TopicQuadratics DescriptionThis image features a table with time versus speed data, along with a graph that explains finding distance by calculating the area under a triangular region. To find the distance traveled over a period, calculate the area of the triangular region. The use of math clip art aids in understanding by connecting theoretical concepts with practical applications. Teacher's Script: "Notice how we find distance using the triangle area. How does this connect to what we've learned about motion?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
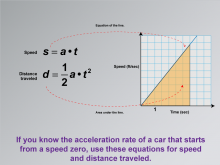
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 17 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 17TopicQuadratics DescriptionThis image displays a graph with speed versus time, highlighting the equation of the line and the area under it. It emphasizes using these equations when acceleration starts from zero. If you know the acceleration rate of a car that starts from speed zero, use these equations for speed and distance traveled. The use of math clip art provides visual clarity in understanding how equations model motion from rest. Teacher's Script: "Notice these equations—how do they help us understand acceleration from rest?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
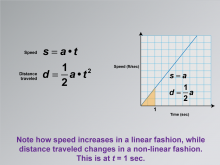
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 18 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 18TopicQuadratics DescriptionThis image shows a graph with speed on the y-axis and time on the x-axis. The equations for speed and distance traveled are given as s = a⋅t and d = 1/2at2. The graph illustrates how speed increases linearly, while distance traveled follows a non-linear path. Math clip art like this helps students understand the difference between linear and quadratic relationships in real-world contexts. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
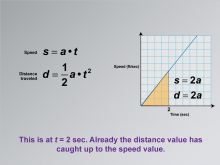
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 19 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 19TopicQuadratics DescriptionThis image shows a graph similar to the previous image but at t = 2 seconds. The equations are updated to s = 2a and d = 2a, indicating that distance has caught up with speed. The use of math clip art provides visual clarity in understanding dynamic interactions between speed and distance over time. Teacher's Script: "At two seconds, notice how distance catches up to speed. What does this mean for our understanding of motion?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
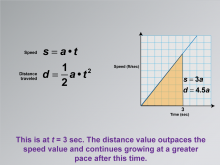
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 20 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 20TopicQuadratics DescriptionThis image depicts a graph of speed versus time with no initial velocity. The equations shown are s = a⋅t for speed and d = 1/2at2 for distance traveled. At t = 3 seconds, the graph highlights that distance outpaces speed. The use of math clip art helps students visualize how distance can grow faster than speed under certain conditions. Teacher's Script: "At three seconds, see how distance outpaces speed? Let's explore why this happens." |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
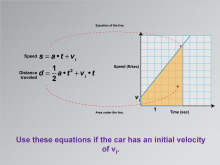
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 21 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 21TopicQuadratics DescriptionThis image shows a graph with a line representing speed as a function of time, with initial velocity. The equations for speed are s = a⋅t+vi and for distance traveled are d= 1/2at2 +vi •t. The graph illustrates the area under the line, indicating distance. The use of math clip art provides students with visual tools to understand how initial velocity affects motion over time. Teacher's Script: "Notice how initial velocity changes the graph. How does this affect our calculations for distance?" |
Graphs of Linear Functions and Graphs of Quadratic Functions |

|
Math Clip Art: Slope vs. Rate | Math Clip Art: Slope vs. Rate In these clip art images, show students the difference between ratios and rates. These images are useful when talking about slope as both a ratio and a rate. In particular, this is useful when talking about slope as a rate of change. |
Slope and Ratios and Rates |
|
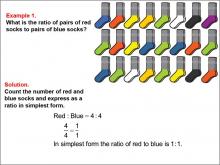
Math Example--Ratios and Rates--Example 1 | Math Example--Ratios and Rates--Example 1TopicRatios and Rates DescriptionThis math example focuses on understanding ratios using colored socks. The image displays a collection of red and blue socks, and students are asked to determine the ratio of red socks to blue socks. The solution demonstrates that there are 4 pairs of red socks and 4 pairs of blue socks, resulting in a ratio of 4 : 4, which simplifies to 1 : 1. |
Ratios and Rates |
|
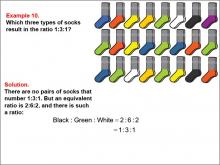
Math Example--Ratios and Rates--Example 10 | Math Example--Ratios and Rates--Example 10TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 3 : 1. |
Ratios and Rates |
|
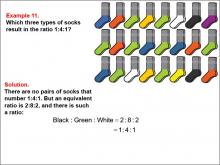
Math Example--Ratios and Rates--Example 11 | Math Example--Ratios and Rates--Example 11TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 4 : 1. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 12 | Math Example--Ratios and Rates--Example 12TopicRatios and Rates DescriptionThis example explores the concept of similar triangles using ratios. The image shows a right triangle with sides labeled as 9, 12, and 15 units. Students are asked to determine if this triangle is similar to a standard 3-4-5 Pythagorean triplet triangle. Understanding similar triangles is an important application of ratios in geometry. This example demonstrates how ratios can be used to compare the sides of triangles and determine similarity. By scaling the sides of a known triangle (3-4-5) and comparing them to the given triangle, students can see how ratios maintain proportionality in similar shapes. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 13 | Math Example--Ratios and Rates--Example 13TopicRatios and Rates DescriptionThis example focuses on verifying the similarity of triangles using ratios. The image shows a right triangle with sides labeled 25, 60, and 65 units. Students are guided through a step-by-step process to determine if this triangle is similar to a 5-12-13 right triangle. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 14 | Math Example--Ratios and Rates--Example 14TopicRatios and Rates DescriptionThis example explores the concept of special right triangles using ratios. The image shows a right triangle with sides labeled 3, 3 2 2 , and 6 units. Students are guided through a step-by-step process to verify if this triangle is similar to a 30°-60°-90° triangle. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 15 | Math Example--Ratios and Rates--Example 15TopicRatios and Rates |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 16 | Math Example--Ratios and Rates--Example 16TopicRatios and Rates DescriptionThis example focuses on converting units of speed and calculating rates. The image shows a car and calculations for converting speed from miles per hour to feet per second, given the distance traveled in miles and time in minutes. Understanding unit conversions and rate calculations is crucial in many real-world applications, particularly in physics and engineering. This example demonstrates how to use ratios to convert between different units of speed, showcasing the practical application of mathematical concepts in everyday scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 17 | Math Example--Ratios and Rates--Example 17TopicRatios and Rates DescriptionThis example explores the concept of unit rates using the cost of gasoline. The image shows a red gasoline container, and students are asked to calculate the cost per gallon of gas given the total cost and volume. Understanding unit rates is a fundamental skill in mathematics with numerous real-world applications. This example demonstrates how to calculate a unit rate by dividing the total cost by the total quantity, illustrating the practical use of division in everyday scenarios like purchasing gasoline. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 18 | Math Example--Ratios and Rates--Example 18TopicRatios and Rates DescriptionThis example focuses on calculating unit rates in a restaurant context. The image shows a hamburger, and students are asked to determine the cost per pound of ground beef given the total cost and weight purchased. Understanding unit rates is essential in various real-world scenarios, particularly in business and economics. This example illustrates how to calculate a unit rate by dividing the total cost by the total quantity, demonstrating the practical application of division in a restaurant supply context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 19 | Math Example--Ratios and Rates--Example 19TopicRatios and Rates DescriptionThis example explores the concept of flow rates using a backyard pool scenario. The image shows a backyard pool, and students are asked to calculate the rate of water flow in gallons per minute given the pool's capacity and the time taken to fill it. Understanding flow rates is important in various fields, including engineering and physics. This example demonstrates how to calculate a rate by dividing the total volume by the total time, illustrating the practical application of division in real-world scenarios involving fluid dynamics. |
Ratios and Rates |
|
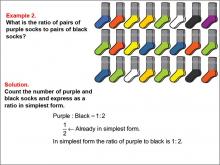
Math Example--Ratios and Rates--Example 2 | Math Example--Ratios and Rates--Example 2TopicRatios and Rates DescriptionThis example explores ratios using purple and black socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to black socks. The solution reveals that there is 1 pair of purple socks and 2 pairs of black socks, resulting in a ratio of 1 : 2, which is already in its simplest form. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 20 | Math Example--Ratios and Rates--Example 20TopicRatios and Rates DescriptionThis example focuses on unit conversion using the height of the Statue of Liberty. The image shows the Statue of Liberty, and students are asked to convert its height from feet to inches. Understanding unit conversions is crucial in many fields, including science, engineering, and everyday life. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 21 | Math Example--Ratios and Rates--Example 21TopicRatios and Rates DescriptionThis example focuses on unit conversion, specifically converting the height of the Statue of Liberty from feet to yards. The image shows the iconic Statue of Liberty, providing a real-world context for the mathematical problem. Understanding unit conversions is crucial in many fields, including engineering, science, and everyday life. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division and multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 22 | Math Example--Ratios and Rates--Example 22TopicRatios and Rates DescriptionThis example explores unit conversion, specifically converting the height of the Statue of Liberty from feet to miles. The image depicts the Statue of Liberty, providing a tangible reference for the mathematical problem. Understanding unit conversions, especially between widely different scales like feet and miles, is important in various fields such as geography, engineering, and urban planning. This example showcases how to use a conversion factor to change units, demonstrating the practical application of division and multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 23 | Math Example--Ratios and Rates--Example 23TopicRatios and Rates DescriptionThis example focuses on unit conversion, specifically converting the height of columns from inches to feet. The image shows columns, providing a visual context for the mathematical problem. Understanding unit conversions between inches and feet is crucial in many practical applications, including construction, interior design, and everyday measurements. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division and multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 24 | Math Example--Ratios and Rates--Example 24TopicRatios and Rates DescriptionThis example explores unit conversion in a sports context, specifically converting a quarterback's pass distance from yards to feet. The image shows a silhouette of a quarterback throwing a football, providing a real-world scenario for the mathematical problem. Understanding unit conversions between yards and feet is crucial in many sports, especially American football. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in sports-related measurement scenarios. |
Ratios and Rates |
|
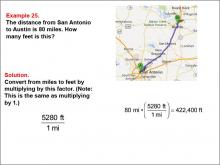
Math Example--Ratios and Rates--Example 25 | Math Example--Ratios and Rates--Example 25TopicRatios and Rates DescriptionThis example focuses on unit conversion in a geographic context, specifically converting the distance between San Antonio and Austin from miles to feet. The image shows a map of the route between these two Texas cities, providing a real-world scenario for the mathematical problem. Understanding unit conversions between miles and feet is important in various fields, including geography, transportation, and urban planning. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in distance-related measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 26 | Math Example--Ratios and Rates--Example 26TopicRatios and Rates DescriptionThis example focuses on time unit conversion, specifically converting hours to minutes in the context of a standardized test duration. The image shows a clock, providing a visual representation of time for the mathematical problem. Understanding time unit conversions is crucial in many aspects of daily life, including scheduling, time management, and test-taking. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in time-related scenarios. |
Ratios and Rates |
|
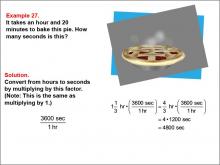
Math Example--Ratios and Rates--Example 27 | Math Example--Ratios and Rates--Example 27TopicRatios and Rates DescriptionThis example explores time unit conversion, specifically converting hours and minutes to seconds in the context of baking a pie. The image shows a steaming pie, providing a real-world scenario for the mathematical problem. Understanding time unit conversions, especially when dealing with mixed units, is important in various fields such as cooking, manufacturing, and project management. This example demonstrates how to use conversion factors to change units, illustrating the practical application of multiplication in time-related scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 28 | Math Example--Ratios and Rates--Example 28TopicRatios and Rates DescriptionThis example focuses on time unit conversion in a sports context, specifically converting minutes and seconds to seconds for a horse race lap time. The image shows a horse, providing a visual context for the mathematical problem. Understanding time unit conversions is crucial in many sports, especially those involving racing and timed events. This example demonstrates how to use conversion factors to change units and add different time units, illustrating the practical application of multiplication and addition in sports-related time scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 29 | Math Example--Ratios and Rates--Example 29TopicRatios and Rates DescriptionThis example explores time unit conversion in an IT context, specifically converting seconds to minutes for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem. Understanding time unit conversions is crucial in many technological fields, especially in IT and user experience analysis. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division in time-related measurement scenarios. It also introduces the concept of mixed numbers in the result. |
Ratios and Rates |
|
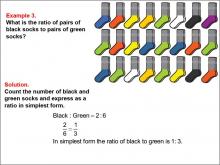
Math Example--Ratios and Rates--Example 3 | Math Example--Ratios and Rates--Example 3TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks. The image displays a collection of socks, and students are tasked with determining the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 6 pairs of green socks, resulting in a ratio of 2 : 6, which simplifies to 1 : 3. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 30 | Math Example--Ratios and Rates--Example 30TopicRatios and Rates DescriptionThis example focuses on time unit conversion in an IT context, specifically converting seconds to hours for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 31 | Math Example--Ratios and Rates--Example 31TopicRatios and Rates DescriptionThis example focuses on temperature unit conversion, specifically converting Celsius to Fahrenheit for the boiling point of water. The image shows a beaker of boiling water, providing a visual context for the mathematical problem. Understanding temperature unit conversions is crucial in many scientific fields, including chemistry, physics, and meteorology. This example demonstrates how to use a conversion formula to change units, illustrating the practical application of mathematical equations in real-world temperature scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 32 | Math Example--Ratios and Rates--Example 32TopicRatios and Rates DescriptionThis example explores temperature unit conversion, specifically converting Fahrenheit to Celsius for the freezing point of water. The image shows icicles, providing a visual representation of the freezing temperature for the mathematical problem. |
Ratios and Rates |
|
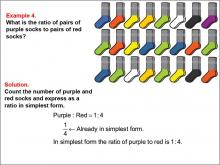
Math Example--Ratios and Rates--Example 4 | Math Example--Ratios and Rates--Example 4TopicRatios and Rates DescriptionThis example explores ratios using purple and red socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to red socks. The solution reveals that there is 1 pair of purple socks and 4 pairs of red socks, resulting in a ratio of 1 : 4, which is already in its simplest form. |
Ratios and Rates |
|
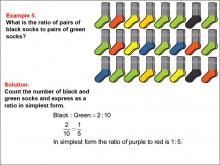
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |