Illustrative Math Alignment: Grade 7 Unit 5

Rational Number Arithmetic

Lesson 12: Negative Rates

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topics
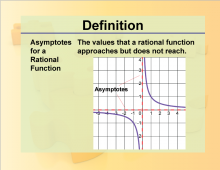
Definition--Rationals and Radicals--Geometric Mean	Geometric Mean Topic Rationals and Radicals Definition The geometric mean of two numbers is the square root of their product. Description The geometric mean is an example of using radical expressions to solve a problem. It provides a measure of central tendency that is particularly useful in situations where the numbers are multiplied together rather than added. In geometry, the geometric mean appears in various theorems and constructions. It is also used in finance and statistics to calculate average growth rates and to compare different sets of data.	Radical Expressions
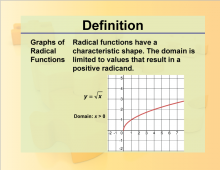
Definition--Rationals and Radicals--Graphs of Radical Functions	Graphs of Radical Functions Topic Rationals and Radicals Definition Graphs of radical functions are visual representations of equations involving radicals. Description Graphs of radical functions are crucial in the study of Radical Numbers, Expressions, Equations, and Functions. They provide a visual understanding of how these functions behave, including their domains, ranges, and key features such as intercepts and asymptotes.	Radical Functions and Equations
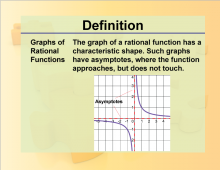
Definition--Rationals and Radicals--Graphs of Rational Functions	Graphs of Rational Functions Topic Rationals and Radicals Definition Graphs of rational functions are visual representations of equations involving rational expressions. Description Graphs of rational functions are fundamental in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of these functions, including their asymptotes, intercepts, and regions of increase and decrease.	Rational Functions and Equations
Definition--Rationals and Radicals--Horizontal Asymptote	Horizontal Asymptote Topic Rationals and Radicals Definition A horizontal asymptote is a horizontal line that a rational function graph approaches as the input values become very large or very small. Description Horizontal asymptotes are an important concept in the study of Rational Numbers, Expressions, Equations, and Functions. They indicate the value that a function approaches as the input grows infinitely large or small. Understanding horizontal asymptotes is crucial for graphing rational functions accurately and for analyzing their long-term behavior.	Rational Functions and Equations
Definition--Rationals and Radicals--Inverse Variation	Inverse Variation Topic Rationals and Radicals Definition Inverse variation describes a relationship between two variables in which the product is a constant. When one variable increases, the other decreases proportionally.	Rational Functions and Equations
Definition--Rationals and Radicals--Irrational Number	Irrational Number Topic Rationals and Radicals Definition An irrational number is a number that cannot be expressed as a ratio of two integers. Its decimal form is non-repeating and non-terminating.	Rational Expressions
Definition--Rationals and Radicals--Irrational Number 2	Irrational Number 2 Topic Rationals and Radicals Definition An irrational number is a number that cannot be expressed as a ratio of two integers. Its decimal form is non-repeating and non-terminating.	Rational Expressions
Definition--Rationals and Radicals--Laws of Rational Exponents	Laws of Rational Exponents Topic Rationals and Radicals Definition The laws of rational exponents describe how to handle exponents that are fractions, including rules for multiplication, division, and raising a power to a power. Description The Laws of Rational Exponents are vital in the study of Rational Numbers, Expressions, Equations, and Functions. These laws provide a framework for simplifying expressions involving exponents that are fractions. For example, the law $$a^{m/n} = \sqrt[n]{a^m}$$	Rational Expressions
Definition--Rationals and Radicals--nth Root	nth Root Topic Rationals and Radicals Definition The nth root of a number is a value that, when raised to the power of n, gives the original number. It is denoted as $$\sqrt[n]{a}$$ Description The nth Root is a fundamental concept in the study of Radical Numbers, Expressions, Equations, and Functions. It generalizes the idea of square roots and cube roots to any positive integer n. For example, the cube root of 8 is 2 because $$2^3 = 8$$	Radical Expressions
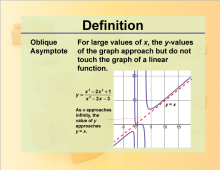
Definition--Rationals and Radicals--Oblique Asymptote	Oblique Asymptote Topic Rationals and Radicals Definition An oblique asymptote is a diagonal line that the graph of a function approaches as the input values become very large or very small. Description Oblique Asymptotes are important in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions where the degree of the numerator is one more than the degree of the denominator. For example, the function $$f(x) = \frac{x^2 + 1}{x}$$	Rational Functions and Equations
Definition--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression	Partial Fraction Decomposition of a Rational Expression Topic Rationals and Radicals Definition Partial fraction decomposition is a method used to express a rational expression as a sum of simpler fractions. Description Partial Fraction Decomposition is a powerful tool in the study of Rational Numbers, Expressions, Equations, and Functions. It involves breaking down a complex rational expression into a sum of simpler fractions, which are easier to integrate or differentiate. For example, the rational function $$\frac{2x+3}{(x+1)(x-2)}$$ can be decomposed into	Rational Expressions
Definition--Rationals and Radicals--Radical Equations	Radical Equations Topic Rationals and Radicals Definition Radical equations are equations in which the variable is inside a radical, such as a square root or cube root. Description Radical Equations are a fundamental aspect of Radical Numbers, Expressions, Equations, and Functions. These equations involve variables within radical signs, such as square roots or cube roots. Solving radical equations typically requires isolating the radical on one side of the equation and then squaring both sides to eliminate the radical. For example, to solve $$\sqrt{x+3} = 5$$ one would square both sides to obtain $$x + 3 = 25$$	Radical Functions and Equations
Definition--Rationals and Radicals--Radical Expression	Radical Expression Topic Rationals and Radicals Definition A radical expression is an expression that contains a radical symbol, which indicates the root of a number. Description Radical Expressions are a core component of Radical Numbers, Expressions, Equations, and Functions. These expressions involve roots, such as square roots, cube roots, or higher-order roots, and are denoted by the radical symbol (√). For example, the expression $$\sqrt{16}$$	Radical Expressions
Definition--Rationals and Radicals--Radical Function	Radical Function Topic Rationals and Radicals Definition A radical function is a function that contains a radical expression with the independent variable in the radicand. Description Radical Functions are a vital part of Radical Numbers, Expressions, Equations, and Functions. These functions involve radicals, such as square roots or cube roots, with the independent variable inside the radical. For example, the function $$f(x) = \sqrt{x}$$	Radical Expressions
Definition--Rationals and Radicals--Radical Symbol	Radical Symbol Topic Rationals and Radicals Definition The radical symbol (√) is used to denote the root of a number, such as a square root or cube root. Description The Radical Symbol is a fundamental notation in the study of Radical Numbers, Expressions, Equations, and Functions. This symbol (√) indicates the root of a number, with the most common being the square root. For example, the expression $$\sqrt{25}$$	Radical Expressions
Definition--Rationals and Radicals--Radicand	Radicand Topic Rationals and Radicals Definition The radicand is the number or expression inside the radical symbol that is being rooted. Description The Radicand is a key component in the study of Radical Numbers, Expressions, Equations, and Functions. It is the number or expression inside the radical symbol that is being rooted. For example, in the expression $$\sqrt{49}$$	Radical Expressions
Definition--Rationals and Radicals--Rational Equations	Rational Equations Topic Rationals and Radicals Definition Rational equations are equations that involve rational expressions, which are fractions containing polynomials in the numerator and denominator. Description Rational Equations are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These equations involve rational expressions, which are fractions containing polynomials in the numerator and denominator. Solving rational equations typically requires finding a common denominator, clearing the fractions, and then solving the resulting polynomial equation. For example, to solve $$\frac{1}{x} + \frac{1}{x+1} = \frac{1}{2}$$	Rational Functions and Equations
Definition--Rationals and Radicals--Rational Exponent	Rational Exponent Topic Rationals and Radicals Definition A rational exponent is an exponent that is a fraction, where the numerator indicates the power and the denominator indicates the root. Description Rational Exponents are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. These exponents are fractions, where the numerator indicates the power and the denominator indicates the root. For example, the expression $$a^{m/n}$$ can be rewritten as $$\sqrt[n]{a^m}$$	Rational Expressions
Definition--Rationals and Radicals--Rational Expressions	Rational Expressions Topic Rationals and Radicals Definition Rational expressions are fractions in which the numerator and/or the denominator are polynomials. Description Rational Expressions are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These expressions are fractions where the numerator and/or the denominator are polynomials. Simplifying rational expressions often involves factoring the polynomials and canceling common factors. For example, the rational expression $$\frac{x^2 - 1}{x - 1}$$ can be simplified to x + 1, provided that $$x \neq 1$$	Rational Expressions
Definition--Rationals and Radicals--Rational Functions	Rational Functions Topic Rationals and Radicals Definition Rational functions are functions that are the ratio of two polynomials. Description Rational Functions are a key concept in the study of Rational Numbers, Expressions, Equations, and Functions. These functions are the ratio of two polynomials, such as $$f(x) = \frac{P(x)}{Q(x)}$$ where P(x) and Q(x) are polynomials. Understanding rational functions involves analyzing their behavior, including identifying asymptotes, intercepts, and discontinuities. For example, the function $$f(x) = \frac{1}{x}$$	Rational Functions and Equations
Definition--Rationals and Radicals--Rational Numbers	Rational Numbers Topic Rationals and Radicals Definition Rational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero.	Rational Functions and Equations
Definition--Rationals and Radicals--Rationalizing a Radical	Rationalizing a Radical Topic Rationals and Radicals Definition Rationalizing a radical is the process of eliminating radicals from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor. Description Rationalizing a Radical is an important technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves eliminating radicals from the denominator of a fraction, which simplifies the expression and often makes it easier to work with or compare to other expressions. For example, to rationalize the denominator of $$\frac{1}{\sqrt{3}}$$	Radical Expressions
Definition--Rationals and Radicals--Rationalizing the Denominator	Rationalizing the Denominator Topic Rationals and Radicals Definition Rationalizing the denominator is the process of eliminating radicals or complex numbers from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor. Description Rationalizing the Denominator is a crucial technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves removing radicals or complex numbers from the denominator of a fraction, which simplifies the expression and often makes it easier to evaluate or compare with other expressions. For example, to rationalize the denominator of	Radical Expressions
Definition--Rationals and Radicals--Simplifying a Radical Expression	Simplifying a Radical Expression Topic Rationals and Radicals Definition Simplifying a radical expression involves reducing the expression to its simplest form by factoring the radicand and removing any perfect square factors (for square roots) or perfect cube factors (for cube roots). Description Simplifying a Radical Expression is a fundamental skill in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves reducing a radical expression to its simplest form, which often makes it easier to work with and understand. For example, simplifying $$\sqrt{18}$$ results in	Radical Expressions
Definition--Rationals and Radicals--Simplifying a Rational Expression	Simplifying a Rational Expression Topic Rationals and Radicals Definition Simplifying a rational expression involves reducing the fraction to its lowest terms by factoring both the numerator and denominator and canceling common factors. Description Simplifying a Rational Expression is a crucial skill in the study of Rational Numbers, Expressions, Equations, and Functions. This process involves reducing a rational expression to its simplest form by factoring both the numerator and denominator and canceling common factors. For example, simplifying $$\frac{x^2 - 1}{x - 1}$$ results in x + 1 for	Rational Expressions
Definition--Rationals and Radicals--Square Root	Square Root Topic Rationals and Radicals Definition The square root of a number is a value that, when multiplied by itself, gives the number. It is denoted by the radical symbol √.	Radical Expressions
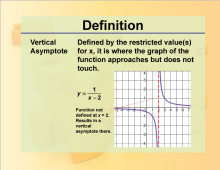
Definition--Rationals and Radicals--Vertical Asymptote	Vertical Asymptote Topic Rationals and Radicals Definition A vertical asymptote is a vertical line that the graph of a function approaches but never reaches as the input values get closer to a certain point. Description Vertical Asymptotes are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions when the denominator equals zero for certain input values, causing the function to approach infinity or negative infinity. For example, the function $$f(x) = \frac{1}{x-2}$$	Rational Functions and Equations
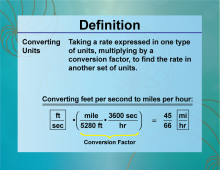
Definition--Ratios, Proportions, and Percents Concepts--Converting Units	Converting Units Topic Ratios, Proportions, and Percents Definition Converting units involves changing a measurement from one unit to another using a conversion factor. Description Converting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios	Equivalent Ratios Topic Ratios, Proportions, and Percents Definition Equivalent ratios are ratios that express the same relationship between quantities. Description Equivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios	Part-to-Part Ratios Topic Ratios, Proportions, and Percents Definition Part-to-part ratios compare different parts of a whole to each other. Description Part-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios	Part-to-Whole Ratios Topic Ratios, Proportions, and Percents Definition Part-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. Description Part-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Rate	Rate Topic Ratios, Proportions, and Percents Definition A rate is a ratio that compares two quantities with different units. Description Rates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratio	Ratio Topic Ratios, Proportions, and Percents Definition A ratio is a comparison of two quantities by division. Description Ratios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions	Ratios and Fractions Topic Ratios, Proportions, and Percents Definition Ratios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. Description Understanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio.	Ratios and Rates
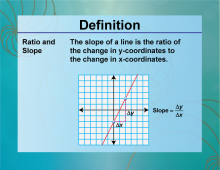
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope	Ratios and Slope Topic Ratios, Proportions, and Percents Definition The slope of a line is a ratio that represents the change in y over the change in x. Description Understanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals	Ratios with Decimals Topic Ratios, Proportions, and Percents Definition Ratios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. Description Ratios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions	Ratios with Fractions Topic Ratios, Proportions, and Percents Definition Ratios with fractions compare two quantities where one or both of the quantities are fractions. Description Ratios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents	Ratios with Percents Topic Ratios, Proportions, and Percents Definition Ratios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. Description Ratios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--The Golden Ratio	The Golden Ratio Topic Ratios, Proportions, and Percents Definition The Golden Ratio is a special number approximately equal to 1.618, often denoted by the Greek letter φ (phi), which appears in various aspects of art, architecture, and nature.	Applications of Ratios, Proportions, and Percents and Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Unit Rate	Unit Rate Topic Ratios, Proportions, and Percents Definition A unit rate is a comparison of any two separate but related measurements when one of the measurements is reduced to a single unit. Description Unit rates are commonly used in everyday life, such as calculating speed (miles per hour), cost per item, or efficiency (miles per gallon). For example, if a car travels 300 miles on 10 gallons of gas, the unit rate is 30 miles per gallon.	Ratios and Rates
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Equivalent Ratios	Visualizing Equivalent Ratios Topic Ratios, Proportions, and Percents Definition Visualizing equivalent ratios involves using diagrams or models to show that two ratios are equivalent. Description Visualizing equivalent ratios is important in fields such as mathematics and engineering, where understanding proportional relationships is crucial. For example, using a double number line or a ratio table can help illustrate that the ratios 2:3 and 4:6 are equivalent.	Ratios and Rates
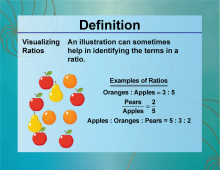
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Ratios	Visualizing Ratios Topic Ratios, Proportions, and Percents Definition Visualizing ratios involves using diagrams or models to represent and understand the relationship between two quantities. Description Visualizing ratios is essential in various fields, such as mathematics, science, and economics, where understanding the relationship between quantities is crucial. For example, using a bar model or a double number line can help illustrate the ratio of 3:4.	Ratios and Rates
Desmos Activity: Slope As Rate of Change	Desmos Activity: Slope As Rate of Change Use this activity to explore slope as a rate of change. In this Desmos activity, the slope of the line is the rate (cost per pound) for purchasing fruit. Students manipulate the slider for m to see the impact on the cost.	Slope and Ratios and Rates
Formulas--Converting Celsius to Fahrenheit	Formulas--Converting Celsius to Fahrenheit The formula for the Converting Celsius to Fahrenheit. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates
Formulas--Converting Days to Hours	Formulas--Converting Days to Hours The formula for Converting Days to Hours. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates
Formulas--Converting Days to Minutes	Formulas--Converting Days to Minutes The formula for Converting Days to Minutes. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates
Formulas--Converting Days to Seconds	Formulas--Converting Days to Seconds The formula for Converting Days to Seconds. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates
Formulas--Converting Degrees to Radians	Formulas--Converting Degrees to Radians The formula for Converting Degrees to Radians. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates
Formulas--Converting Fahrenheit to Celsius	Formulas--Converting Fahrenheit to Celsius The formula for Converting Fahrenheit to Celsius. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates
Formulas--Converting Hours to Minutes	Formulas--Converting Hours to Minutes The formula for Converting Hours to Minutes. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates